数据变异性的度量 - 极差、IQR、方差和标准偏差

来源：DeepHub IMBA
本文约1200字，建议阅读5分钟可变性的最佳衡量标准取决于不同衡量标准和分布水平。

variability被称作变异性或者可变性，它描述了数据点彼此之间以及距分布中心的距离。

可变性有时也称为扩散或者分散。因为它告诉你点是倾向于聚集在中心周围还是更广泛地分散。

低变异性是理想的，因为这意味着可以根据样本数据更好地预测有关总体的信息。高可变性意味着值的一致性较低，因此更难做出预测。在统计学中，我们的目标是测量一组特定数据或一个分布的变异性。简单来说，如果一个分布中的数据值是相同的，那么它没有变异性。

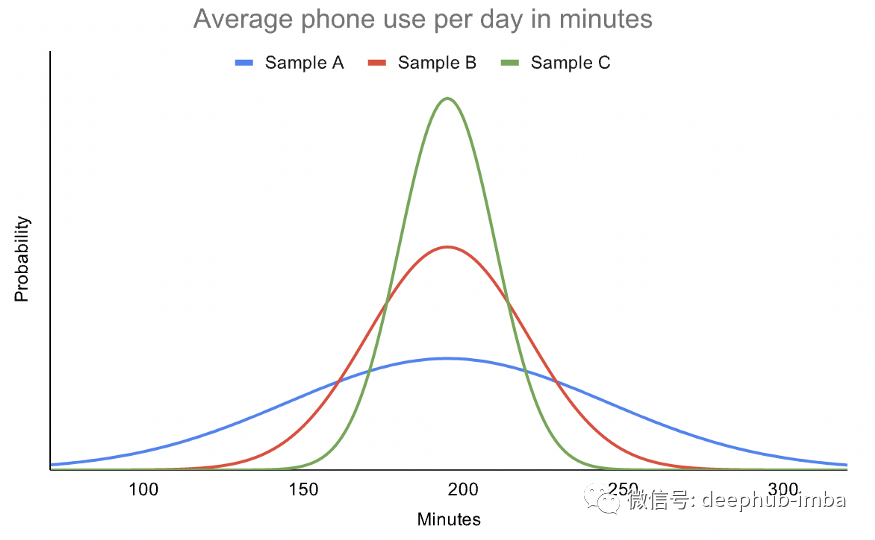
上图中尽管数据服从正态分布，但每个样本都有不同的分布。样品 A 的变异性最大，而样品 C 的变异性最小。

可以使用多种不同的方式对变异度进行度量。

极差（Range）

极差，又称全距，可以显示数据从分布中的最低值到最高值的分布。

例如，考虑以下数字：1、3、4、5、5、6、7、11。对于这组数字，极差是 11-1 或 10。

极差的度量仅使用了 2 个数字因此受异常值影响很大，并且不会提供有关值分布的任何信息。所以它最好与其他方法结合使用。

四分位距（Interquartile range）

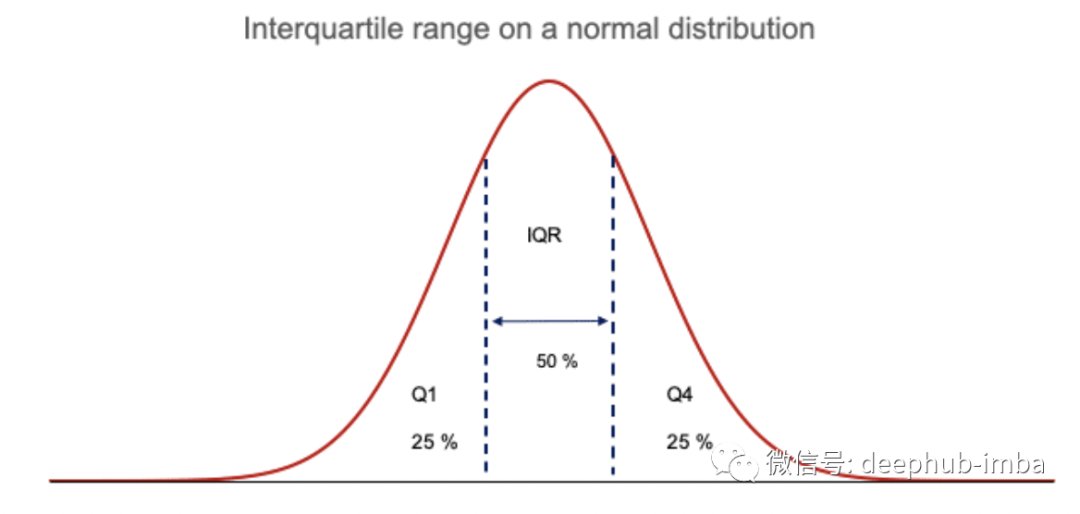
四分位距又被称作四分差，可以提供数据分布中间的分布。

对于从低到高排序的任何分布，四分位距包含数据中一半的值。第一个四分位数 (Q1) 包含前 25% 的值，而第四个四分位数 (Q4) 包含最后 25% 的值。

它衡量数据如何围绕均值分布。基本公式为：IQR = Q3 - Q1。

就像极差一样，四分位距在其计算中仅使用 2 个值。但是IQR受异常值的影响较小：这2个值来自数据集的中间一半，所以不太可能是极端数字。

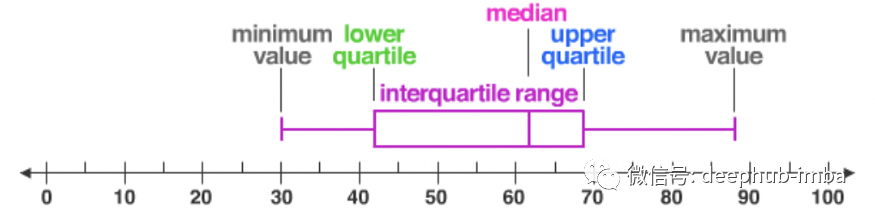
小知识：每个分布都可以使用五个数字摘要进行组织：

• 最低值

• Q1：第 25 个百分位

• Q2：中位数

• Q3：第 75 个百分位

• 最高值 (Q4)

方差（Variance）

方差表示数据集的分布范围，但它是一个抽象数字。它反映了数据集中的分散程度。数据越分散，方差与均值的关系就越大。

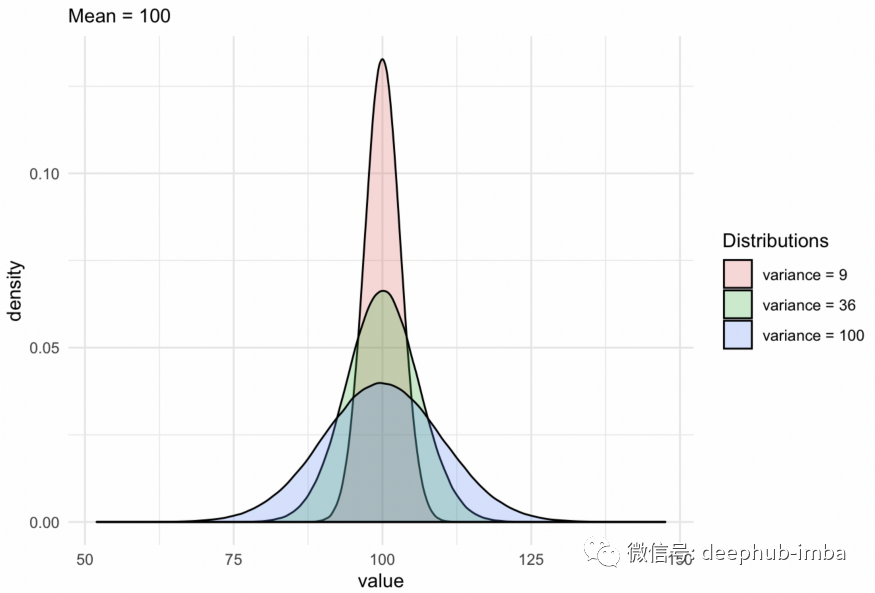
• 小方差 - 数据点往往非常接近均值且彼此非常接近

• 高方差 - 数据点与均值和彼此之间非常分散

• 零方差——所有数据值都相同

标准差（Standard Deviation）

标准偏差是数据集中的平均变异量。它平均表示每个数据点与平均值相差多远。标准差越大，数据集的可变性越大。

为什么使用 n - 1 作为样本标准差？

当拥有总体数据时可以获得总体标准差的准确值。可以从每个总体成员收集数据，因此标准差反映了分布（总体）中的精确变异量。

但当无法获得所有数据时，就可以对整体数据进行抽样（抽样方式这就不详细介绍）。

抽样的结果就被称作样本，样本的作用是对总体的数据进行统计推断的。当使用样本数据时，样本标准差始终用作总体标准差的估计值。在这个公式中使用 n 往往会给你一个有偏差的估计，它总会低估可变性。

将样本 n 减少到 n - 1 会使标准偏差人为地变大，从而提供对变异性的保守估计。虽然这不是无偏估计，但它是对标准差的偏少估计：高估而不是低估样本的可变性更好。

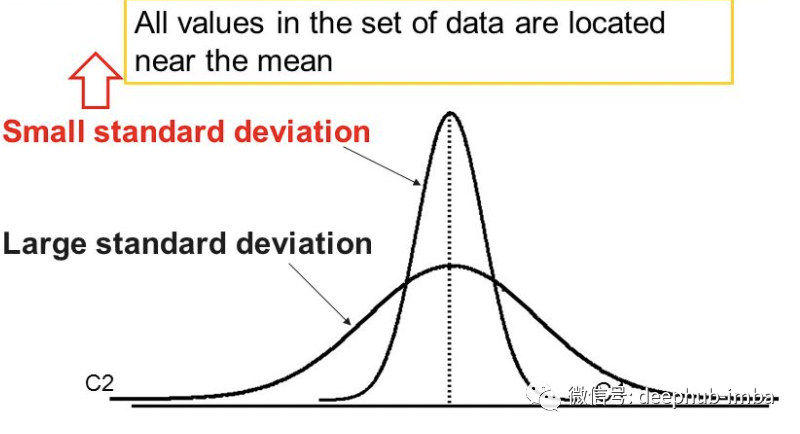
标准差低 - 数据点往往接近平均值 标准差高 - 数据点分布在大极差的值上。

什么是变异性的最佳衡量标准？

可变性的最佳衡量标准取决于不同衡量标准和分布水平。

对于在序数水平上测量的数据，极差和四分位距是唯一合适的变异性度量。

对于更复杂的区间和比率的数据，标准差和方差也适用。

对于正态分布，可以使用所有度量。但标准差和方差是首选，因为它们考虑了整个数据集，但这也意味着它们很容易受到异常值的影响。

对于偏态分布或具有异常值的数据集，四分位距是最好的度量。它受极值影响最小，因为它侧重于数据集中间的部分。

编辑：于腾凯