软件无线电系列——多率信号处理之抽取

本文主要是介绍软件无线电系列——多率信号处理之抽取，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本节目录

一、等效基带谱
二、抽取概念
三、低通信号的整数倍抽取
四、数字带通信号的抽取
1、整带抽取
2、带通信号的正交复抽取
3、带通信号的正交实抽取

本节内容
一、等效基带谱
对于任何采样频率为fs的实采样信号，无论是Nyquist采样还是带通采样，采样信号都可以用统一0～fs/2的等效基带谱来表示。简单点说，模拟频率f和数字频率ω之间存在对应关系，用公式来表示:
f=(fs/2π)×ω
在数字域使用0～π的频谱来表示，在模拟域则用0～fs/2的频谱来表示。当然，实际中，在0～fs/2或0～π内会存在多个信号出现，比如下图：
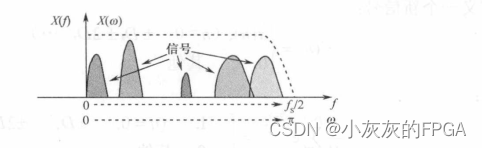
在这里插入图片描述

此处存在5个信号，由此引入多率信号处理，如何从采样速率fs的高速数据流中提取出所需要的窄带信号，并把采样速率降到与窄带信号相一致的较低的采样率，方便后续的信号实时处理。
二、抽取概念
假设上图中，最左边靠近零频的信号是我们所需要的信号，需要把其他信号滤除，通过一个低通滤波器后就可以得到一个窄带的低通信号。滤除后的信号带宽变为原来fs/2的1/D，当然采样速率也降低了，两者之间仍然满足Nyquist低通采样定理，故仍然可以恢复原来的信号。
上述过程中，先用一个低通滤波器进行滤波，再用低采样速率采样，这就是多率信号处理中的抽取。
三、低通信号的整数倍抽取
整数倍抽取是指将原始采样序列x(n)每D个数据抽取一个，形成一个新的序列xD(m)，且xD(m)=x(mD)，其中D为正整数。
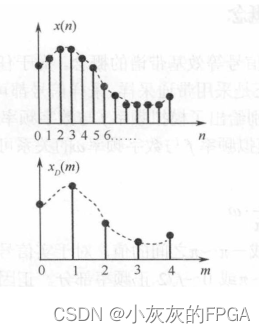
在这里插入图片描述

抽取序列的频谱是抽取前原始序列的频谱经过频移和D倍展开后的D个频谱的叠加和。这种抽取过程中如果原始信号的频谱分量大于π/D,就会产生信号的混叠，比如：
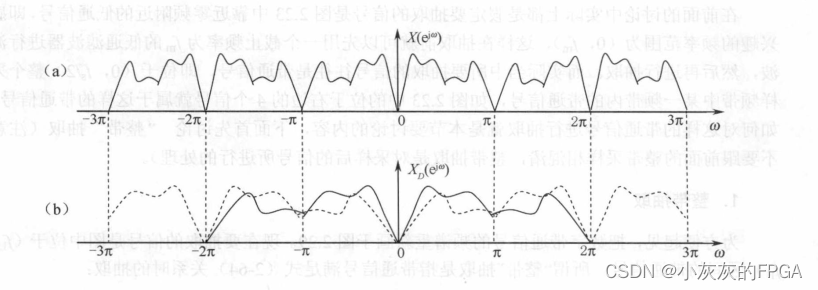
在这里插入图片描述

上图中a是抽取前的信号频谱，b是实际频谱是a中频谱展开2倍后频谱以及频移2π后的频谱的叠加，也就是发送了所谓的频谱混叠。
若在抽取之前，将原始信号的频谱分量控制在π/D以内，通过一个带宽小于π/D的低通滤波器来实现，具体如下：
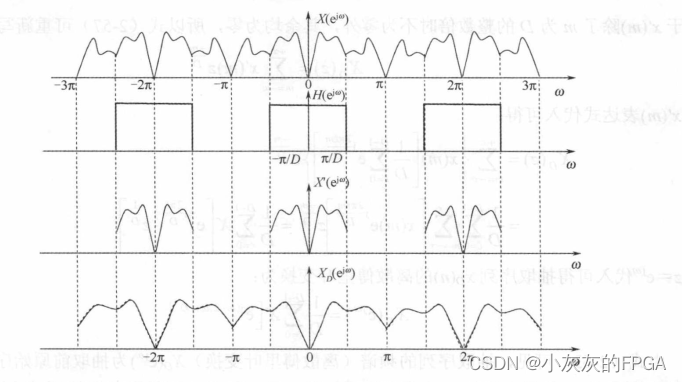
在这里插入图片描述

四、数字带通信号的抽取
1、整带抽取
整带抽取是针对采样后的信号进行的处理。对位于(fL,fH)区间，中心频率为f0的带通信号抽取时候，需要满足带通信号关系式，其公式为：
f0=(fL+fH)/2=((2n+1)/4)×fs’
上式中n为正整数，fs’为经过D倍抽取后的采样率，由此可以得出：
fs’=fs/D=2×(fH-fL)=2B
D=fs/2B
fL+fH=(2n+1)×B
带通信号的最高频率和最低频率是信号带宽的整数倍时候，称为整带抽取，在(0,fs/2)整个数字频带内共有带宽为B的D个子频带。
2、带通信号的正交复抽取
整带抽取必须满足D=fs/2B,但是实际过程中很难满足，因此可以采用频谱搬移，将位于中心频率f0的带通信号搬移到基带，然后利用低通信号的抽取方式进行抽取。
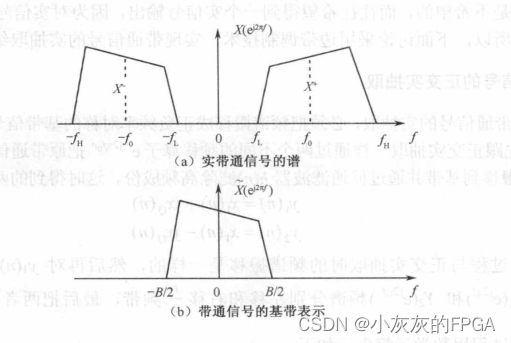
在这里插入图片描述

上述图中a表示一个实带通信号的频谱，是共轭对称的。用一个复信号e^(j2πf0n)乘以原来带通信号x(n)，这样就将a图中的负频率分量搬移至零频，正频率分量搬移至2f0,再使用一个低通滤波器h(n)将2f0处的高频分量滤除，就得到了带通信号的基带表示，如图b所示。之后再进行低通抽取。
在这里插入图片描述

好多人好奇为啥抽取是采用的是2D而不是D?
从带通信号的基带表示图中可以看出，此时的带宽为B，对应的两个正交分量的带宽是B/2，根据公式D=fs/2B，带宽变为一半，因此此处采用2D而不是D。
3、带通信号的正交实抽取
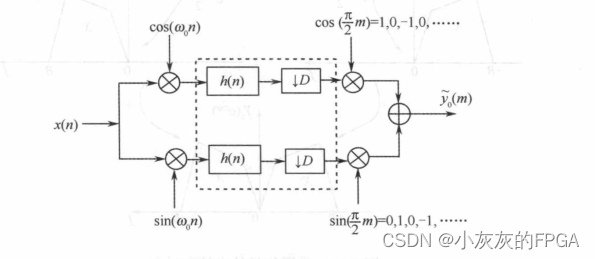
如果为了完成带通信号的实抽取，需要将频谱搬移成正负频率对称的基带信号。具体变化过程如下图:
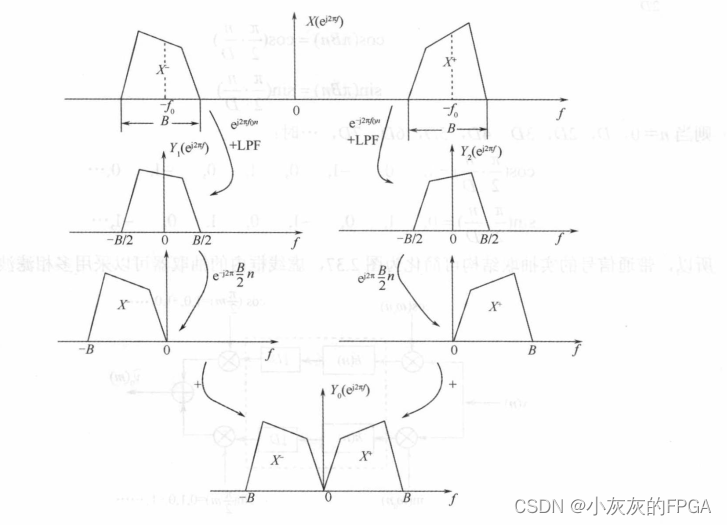
在这里插入图片描述