【图论】Dijkstra单源最短路径-朴素方法-简单模板（迪杰斯特拉算法）

本文主要是介绍【图论】Dijkstra单源最短路径-朴素方法-简单模板（迪杰斯特拉算法），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Dijkstra单源最短路径

问题描述

输入n 表示n个结点，m表示m条边，求编号1的结点到每个点的最短路径

输出从第一个点到第n个点的最短路径

思路

将图g[][]中所有的权值初始化为0x3f表示正无穷
将dist[]中所有的值初始化为0x3f表示从第一个点到所有点的距离默认为无穷
将dist[1]设置为0表示从第一个点到它自己距离为零
执行n(也就是处理n个点的次数)次如下操作:
- 找到所有没有确定最短路径的点中，离1点(初始点)最近的那个
  
  例如: 下面这个图，第一次找到结点1，因为它没有被确定过最短路径，然后更新到达2的路径为新的最短路为2，到达3的最短路为4。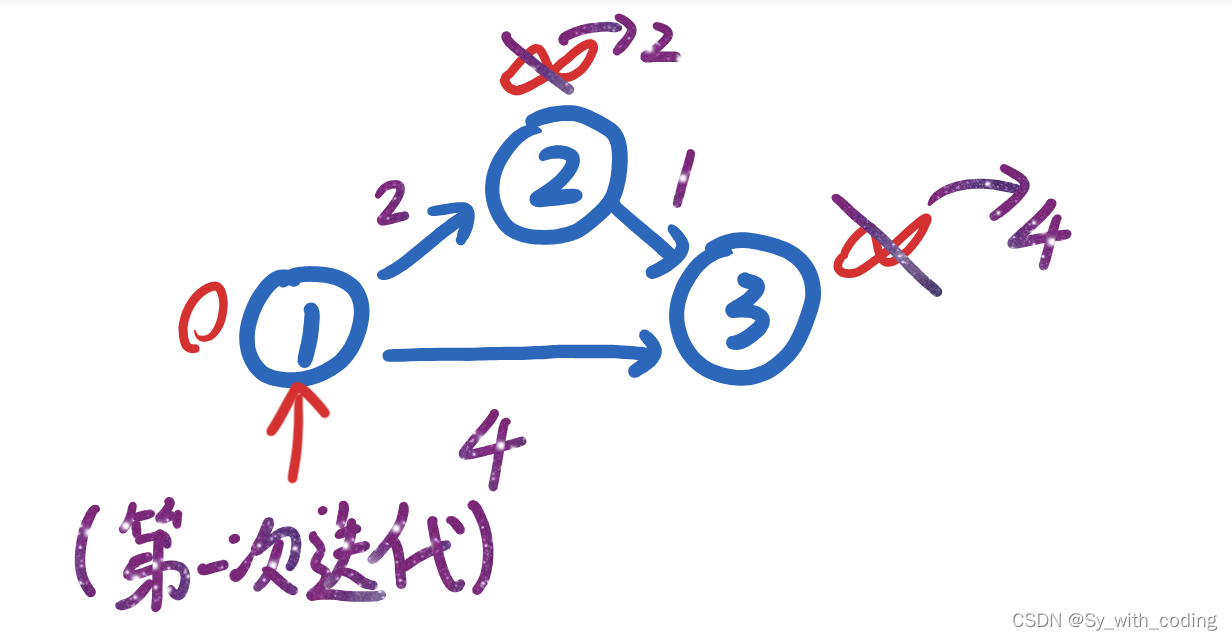

#include <iostream>
#include <cstring>
using namespace std;const int N = 510;		
int g[N][N], dist[N];	//g为邻接矩阵 
bool st[N];	  			//表示结点是否已经确定最短路径 
int n, m;				//n为结点数量，m为边数量 int Dijkstra() {memset(dist, 0x3f, sizeof dist);dist[1] = 0;		//从第一个结点到达第一个结点的最短路径为 0 for (int i = 0; i < n; i++ ) {	//循环 n 次处理 n 个结点 int t = -1;for (int j = 1; j <= n; j++ ) {if (!st[j] && (t == -1 || dist[j] < dist[t])) {	//第一次会选择找到的第一个边然后去找最短的边 t = j;	//寻找没有确定最短路径的点当中 到第一个点最近的点 }}//找到没有确定的最近的点for (int j = 1; j <= n; j++) {dist[j] = min(dist[j], dist[t] + g[t][j]);}//从第一个最近的点开始向后更新最短路径 st[t] = true;	//将确定好最短路径的点设置为true表示已经确定了最短路径 }return dist[n];
}//测试数据:
/*
3 3
1 2 2
1 3 4
2 3 1
*/ int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n >> m; memset(g, 0x3f, sizeof g);while (m -- ) {int u, v, c;cin >> u >> v >> c;g[u][v] = c;	//无重边的情况，如果有重边需要进行取重边的最小值 }int t = Dijkstra();cout << t << endl;
}