本文主要是介绍【三十九】【算法分析与设计】综合练习(5),79. 单词搜索,1219. 黄金矿工,980. 不同路径 III,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
79. 单词搜索
给定一个
m x n二维字符网格board和一个字符串单词word。如果word存在于网格中,返回true;否则,返回false。单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例 1:
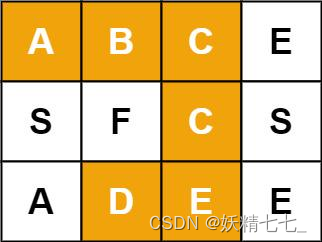
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" 输出:true
示例 2:

输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE" 输出:true
示例 3:

输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB" 输出:false
提示:
m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board和word仅由大小写英文字母组成进阶:你可以使用搜索剪枝的技术来优化解决方案,使其在
board更大的情况下可以更快解决问题?
宏观地看待递归。递归函数,自己调用自己,同一个函数需要表示递归图中任何一个节点。
因此我们需要一些变量与递归函数进行绑定,这些变量帮助我们知道现在的递归函数是在递归图的哪一个节点。
其次,我们还需要能够知道如何从当前的递归节点到达孩子递归节点,这一个过程也需要一些变量的帮助。
因此我们有两个需要做的事情,第一件事是知道当前递归函数代表递归图的哪一个节点。
第二件事是知道如何从当前递归图节点到达孩子递归图节点。
bool dfs(vector<vector<char>>& board, int i, int j, int pos) {
递归函数是这样定义的,它表示当前在递归图的位置(i,j)对应的位置,它如何找到孩子递归图节点,通过pos变量,pos表示word中下一个查找的值,也就是孩子节点对应的值。

对于递归图特定节点,有四个可能的子孩子位置,分别是(i,j)位置的左边,右边,上边,下边。
左边是(i,j-1),右边是(i,j+1),上边是(i-1,j),下边是(i+1,j)。
此时思考如何剪枝,走过的路我们不走,因此需要一个visit数组,用来划分集合,一个集合是走过的路,一个集合是没有走过的路。所以只需要两个不同的值对应即可。可以思考到bool类型。
如果使用int类型,可以对应多个集合,不同的int类型值对应一个集合,例如1对应一个集合,2对应一个集合,等等以此类推。
思考递归出口,如果当前递归图节点,pos==word.size(),说明当前节点已经是最后一个单词的字母。此时直接返回就可以了。
class Solution {
public:bool visit[7][7];int row, col;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};string word;bool exist(vector<vector<char>>& board, string _word) {word = _word;row = board.size();col = board[0].size();for (int i = 0; i < row; i++) {for (int j = 0; j < col; j++) {if (board[i][j] == word[0]) {visit[i][j] = true;if (dfs(board, i, j, 1))return true;visit[i][j] = false;}}}return false;}bool dfs(vector<vector<char>>& board, int i, int j, int pos) {if (pos == word.size()) {return true;}for (int k = 0; k < 4; k++) {int x = i + dx[k];int y = j + dy[k];if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] &&board[x][y] == word[pos]) {visit[x][y] = true;if (dfs(board, x, y, pos + 1))return true;visit[x][y] = false;}}return false;}
};定义全局变量,就不需要给递归函数进行传参。
bool visit[7][7];
定义bool类型的visit数组,进行集合的划分,visit[i][j]对应(i,j)位置,true表示使用过,false表示没有使用过。
int row, col;
定义全局变量row,col分别表示行与列。
int dx[4] = {0, 0, 1, -1}; int dy[4] = {1, -1, 0, 0};
如何快速得到(i,j)位置上下左右四个方位的坐标,利用向量法。
可以知道,这四个位置分别是(i+1,j),(i-1,j),(i,j+1),(i,j-1)。
可以写成(i,j)+(1,0),(i,j)+(-1,0),(i,j)+(0,1),(i,j)+(0,-1)。
只需要表示出增量即可。
dx表示x方向的增量,dy表示y方向的增量。
dx[k],dy[k]共同表示某一个增量组合。
因此dx dy的形式,其中一个增量数组0,0,1,-1。
另一个增量数组在1,-1出现的位置只出现0。另外两个位置出现1,-1。
string word;
小技巧,将函数中的变量变成全局变量,修改名字,在名字前面添加下划线_,然后再全局变量创建一个原名,在函数中赋值过去即可。 bool exist(vector<vector<char>>& board, string _word) { word = _word; row = board.size(); col = board[0].size();
对全局变量的计算,初始化。
for (int i = 0; i < row; i++) { for (int j = 0; j < col; j++) { if (board[i][j] == word[0]) { visit[i][j] = true; if (dfs(board, i, j, 1)) return true; visit[i][j] = false; } } }
遍历递归图中最开始的位置,如果找到word中第一个字符,此时这个位置就是最开始的位置。
注意维护变量,visit。因为visit是全局变量,所以需要手动回溯。
为什么需要回溯?因为这些变量共同表示递归图中某一个位置的节点,当前是这个节点,这些变量就必须维护对应的值。
但是部分节点变量在递归函数中作为形参,此时系统会自动帮我们进行回溯操作。
小技巧:如果是int char等类型,空间小的数据类型,可以放到递归函数中作为形参。
如果是vector空间大的数据类型,放到全局变量中,而不是放到递归韩式作为形参。
因为作为形参每一次都需要重新开辟空间,赋值,如果空间大的这种消耗比较大。
if (dfs(board, i, j, 1)) return true;
注意这条语句,这种用法,是递归寻找某一个特定的值的时候使用,当找到之后,就不需要再递归下去了。
如果找到了,就返回true,如果递归图中子节点找到了,当前节点就不需要再递归其他可能性了,直接返回true。
可以理解为,定义递归函数bool表示当前递归节点树,中是否能够找到。true表示找到了。
如果遍历完,没有返回true,说明所有递归图节点树都没有找到,返回false。 return false; bool dfs(vector<vector<char>>& board, int i, int j, int pos) { if (pos == word.size()) { return true; }
递归的出口,pos表示递归图子节点的可能性。pos==word.size()表示当前节点就是最后一个字母,此时找到了序列,直接返回true。
for (int k = 0; k < 4; k++) { int x = i + dx[k]; int y = j + dy[k]; if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] && board[x][y] == word[pos]) { visit[x][y] = true; if (dfs(board, x, y, pos + 1)) return true;
如果递归图子树找到了,不需要继续递归下去了,直接返回true。
visit[x][y] = false; } } return false;
如果当前节点的所有子树都没有找到,说明当前节点也找不到,返回false。
1219. 黄金矿工
你要开发一座金矿,地质勘测学家已经探明了这座金矿中的资源分布,并用大小为
m * n的网格grid进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量;如果该单元格是空的,那么就是0。为了使收益最大化,矿工需要按以下规则来开采黄金:
每当矿工进入一个单元,就会收集该单元格中的所有黄金。
矿工每次可以从当前位置向上下左右四个方向走。
每个单元格只能被开采(进入)一次。
不得开采(进入)黄金数目为
0的单元格。矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。
示例 1:
输入:grid = [[0,6,0],[5,8,7],[0,9,0]] 输出:24 解释: [[0,6,0], [5,8,7], [0,9,0]] 一种收集最多黄金的路线是:9 -> 8 -> 7。
示例 2:
输入:grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]] 输出:28 解释: [[1,0,7], [2,0,6], [3,4,5], [0,3,0], [9,0,20]] 一种收集最多黄金的路线是:1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。
提示:
1 <= grid.length, grid[i].length <= 15
0 <= grid[i][j] <= 100最多 25 个单元格中有黄金。
class Solution {
public:int row, col;bool visit[16][16];int ret;int getMaximumGold(vector<vector<int>>& grid) {row = grid.size(), col = grid[0].size();for (int i = 0; i < row; i++)for (int j = 0; j < col; j++) {if (grid[i][j] != 0) {visit[i][j] = true;dfs(grid, i, j, grid[i][j]);visit[i][j] = false;}}return ret;}int dx[4] = {0, 0, -1, 1}, dy[4] = {1, -1, 0, 0};void dfs(vector<vector<int>>& grid, int i, int j, int path) {ret = max(ret, path);for (int k = 0; k < 4; k++) {int x = i + dx[k], y = j + dy[k];if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] &&grid[x][y] != 0) {visit[x][y] = true;dfs(grid, x, y, path + grid[x][y]);visit[x][y] = false;}}}
};定义全局变量,这样就不需要给递归函数传参数了。
int row, col;
row表示行数,col表示列数。
bool visit[16][16];
划分集合,用来表示(i,j)位置是否被使用,true被使用,false没有被使用。
int ret;
记录结果。
int getMaximumGold(vector<vector<int>>& grid) {
row = grid.size(), col = grid[0].size();
给row和col初始化。
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++) {
两层for循环遍历最开始递归图的节点。
if (grid[i][j] != 0) {
visit[i][j] = true;
dfs(grid, i, j, grid[i][j]);
这里没有使用bool,返回true的用法,是因为我需要递归所有情况,找到一种情况之后还需要继续递归。
visit[i][j] = false;
手动回溯。
int dx[4] = {0, 0, -1, 1}, dy[4] = {1, -1, 0, 0};
定义增量数组,用来表示(i,j)的四个方位。
void dfs(vector<vector<int>>& grid, int i, int j, int path) {
ret = max(ret, path);
path表示递归图当前节点的有效路径。ret记录所有情况下的最大值。
for (int k = 0; k < 4; k++) {
int x = i + dx[k], y = j + dy[k];
if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] &&
grid[x][y] != 0) {
如果x,y位置没有越界,并且没有没使用过,并且值不为0,此时是合法位置。
visit[x][y] = true;
dfs(grid, x, y, path + grid[x][y]);
visit[x][y] = false;
980. 不同路径 III
在二维网格
grid上,有 4 种类型的方格:
1表示起始方格。且只有一个起始方格。
2表示结束方格,且只有一个结束方格。
0表示我们可以走过的空方格。
-1表示我们无法跨越的障碍。返回在四个方向(上、下、左、右)上行走时,从起始方格到结束方格的不同路径的数目。
每一个无障碍方格都要通过一次,但是一条路径中不能重复通过同一个方格。
示例 1:
输入:[[1,0,0,0],[0,0,0,0],[0,0,2,-1]] 输出:2 解释:我们有以下两条路径: (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2) (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)
示例 2:
输入:[[1,0,0,0],[0,0,0,0],[0,0,0,2]] 输出:4 解释:我们有以下四条路径: (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3) (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3) (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3) (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)
示例 3:
输入:[[0,1],[2,0]] 输出:0 解释: 没有一条路能完全穿过每一个空的方格一次。 请注意,起始和结束方格可以位于网格中的任意位置。
提示:
1 <= grid.length * grid[0].length <= 20
class Solution {
public:int row, col; // 定义行数和列数int visit[21][21]; // 访问标记数组,记录网格中的位置是否被访问过int step; // 步数计数器,记录从起点到终点需要经过的格子数量int ret; // 结果计数器,记录所有满足条件的路径数量int uniquePathsIII(vector<vector<int>>& grid) {row = grid.size(), col = grid[0].size(); // 初始化行数和列数int bx, by; // 起点的坐标for (int i = 0; i < row; i++)for (int j = 0; j < col; j++) {if (grid[i][j] == 0)step++; // 如果格子为0,说明是空格,需要经过,步数加1else if (grid[i][j] == 1)bx = i, by = j; // 如果格子为1,说明是起点,记录起点坐标}step += 2; // 加上起点和终点的格子visit[bx][by] = true; // 标记起点已访问dfs(grid, bx, by, 1); // 从起点开始进行深度优先搜索return ret; // 返回所有满足条件的路径数量}int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1}; // 方向数组,用于实现上下左右移动void dfs(vector<vector<int>>& grid, int i, int j, int count) {if (grid[i][j] == 2) { // 如果当前格子是终点if (step == count)ret++; // 如果当前路径长度等于所需步数,结果加1return;}for (int k = 0; k < 4; k++) { // 遍历四个方向int x = i + dx[k], y = j + dy[k]; // 计算下一个格子的坐标if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] &&grid[x][y] != -1) { // 确保下一个格子在网格内,未被访问过,且不是障碍物visit[x][y] = true; // 标记为已访问dfs(grid, x, y, count + 1); // 递归搜索下一个格子visit[x][y] = false; // 回溯,取消标记}}}
};
结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
这篇关于【三十九】【算法分析与设计】综合练习(5),79. 单词搜索,1219. 黄金矿工,980. 不同路径 III的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






