本文主要是介绍游戏公司面试题系列-CocosCreator实现虚拟摇杆控制角色移动中心旋转自转小球割草旋转逻辑,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
游戏公司面试题系列-CocosCreator实现虚拟摇杆控制角色移动&中心旋转自转小球&割草旋转逻辑<!!!文章末尾有完整代码下载链接地址!!!>
Hello大家好!今天我们来用最新的CocosCreator3.8.2版本完成<一些游戏公司面试题>
1、实现一下横版过关、街机类游戏中用来控制角色操作的虚拟摇杆,咱们把他封装成一个可复用的组件;
2、实现一个小球围绕某个中心点旋转自转的逻辑<在有些公司面试中经常用到>;
3、另外做一个类似割草游戏的攻击旋转的延展;

演示效果如下:


环境要求:
1、Mac/Windows
2、CocosCreator3.8.2<或以上>
3、VsCode
B站演示地址如下:
效果演示地址
<!!!文章末尾有完整代码下载链接地址!!!>
大致展示一下主要实现思路的代码逻辑如下:
数学概念==>
下面要引入两个数学概念,一个是正弦余弦和正切,一个是角度制和弧度制
正弦 余弦 正切
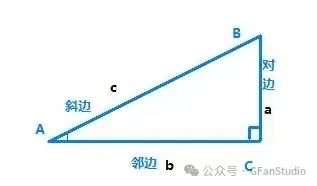
如图,在Rt△ABC中,∠C = 90°,斜边为c,长的直角边为b,短的直角边为a。
正弦
我们把∠A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即
sinA = ∠A的对边 / ∠A的斜边 = a / c
余弦
我们把∠A的邻边与斜边的比叫做∠A的余弦(cosine),记作cosA,即
cosA = ∠A的邻边 / ∠A的斜边 = b / c
正切
我们把∠A的对边与邻边的比叫做∠A的正切(tangent),记作tanA,即
tanA = ∠A的对边 / ∠A的邻边 = a / b
对于tanA有一个公式
tanA = sinA / cosA
也就是
a / b = (a / c) / (b / c)
a / b = (a / c) * (c / b)
等号右边上下两个c约掉了
也就只剩下a / b = a / b


角度制和弧度制
每个角度都有一个对应的弧度值
既然已经有角度制了,为什么还要有弧度制呢
因为代码里Math中用的三角函数都是弧度制,代码只认弧度制,不认角度制180°角的弧度值是π,
由此可以得出公式==>
弧度 = 角度 / 180° * π
角度 = 弧度 / π * 180°
也可以写成==>
弧度 = π / 180° * 角度
角度 = 180° / π * 弧度
<!!!文章末尾有完整代码下载链接地址!!!>
1、小球围绕中点旋转环绕:
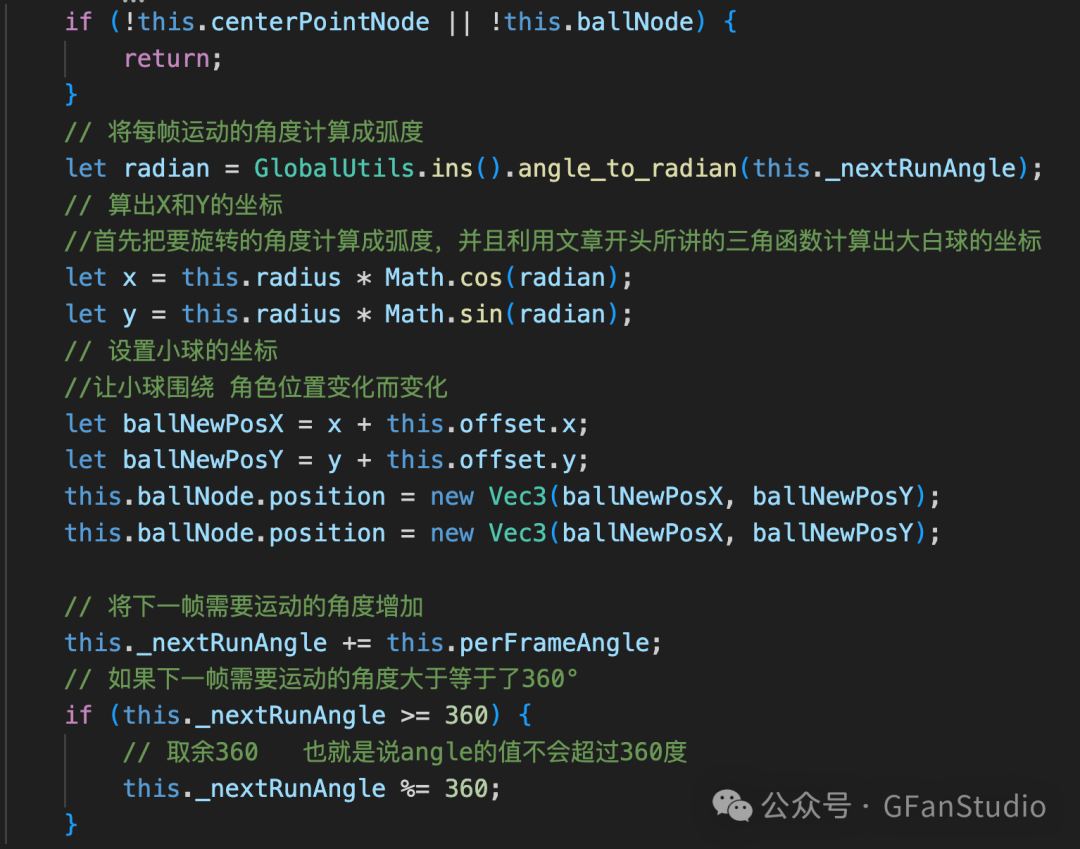
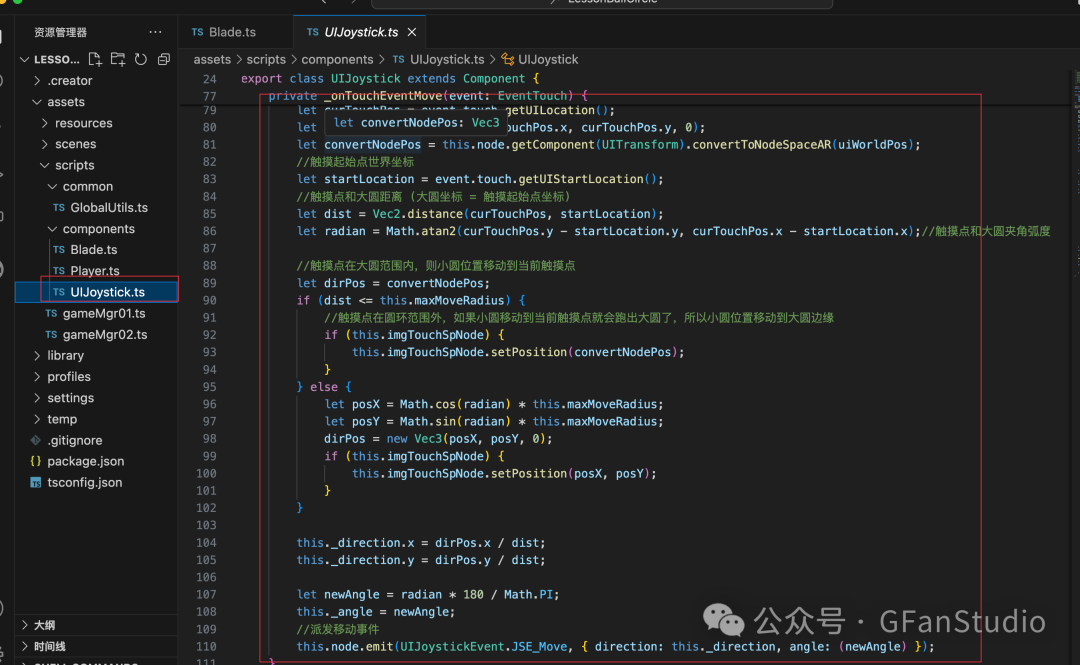
2、实现虚拟摇杆主要代码逻辑如下:
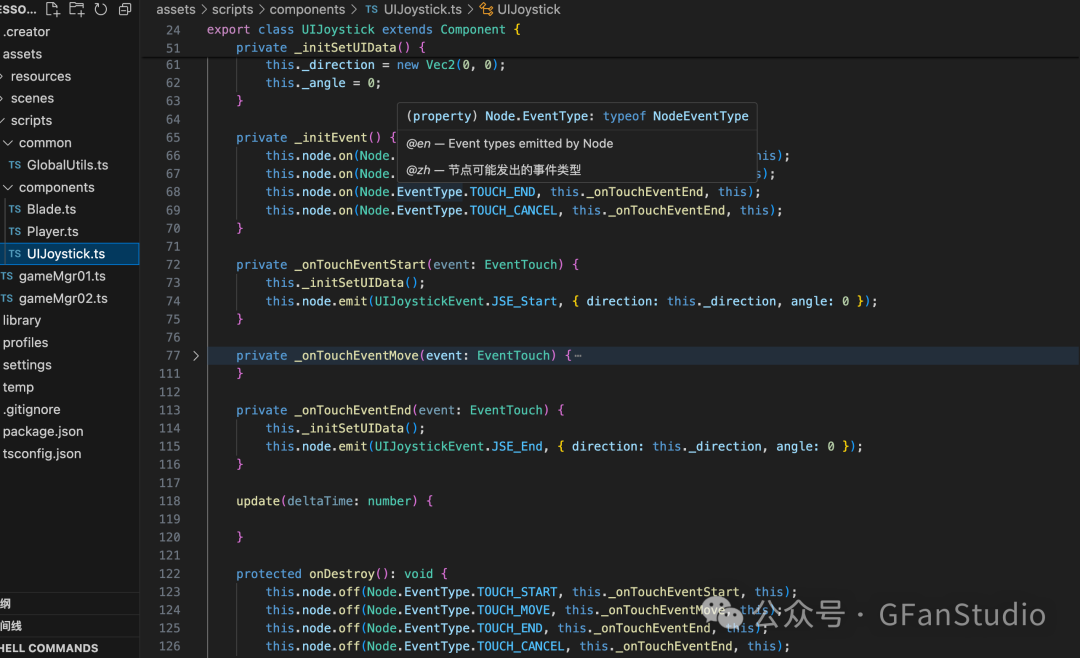
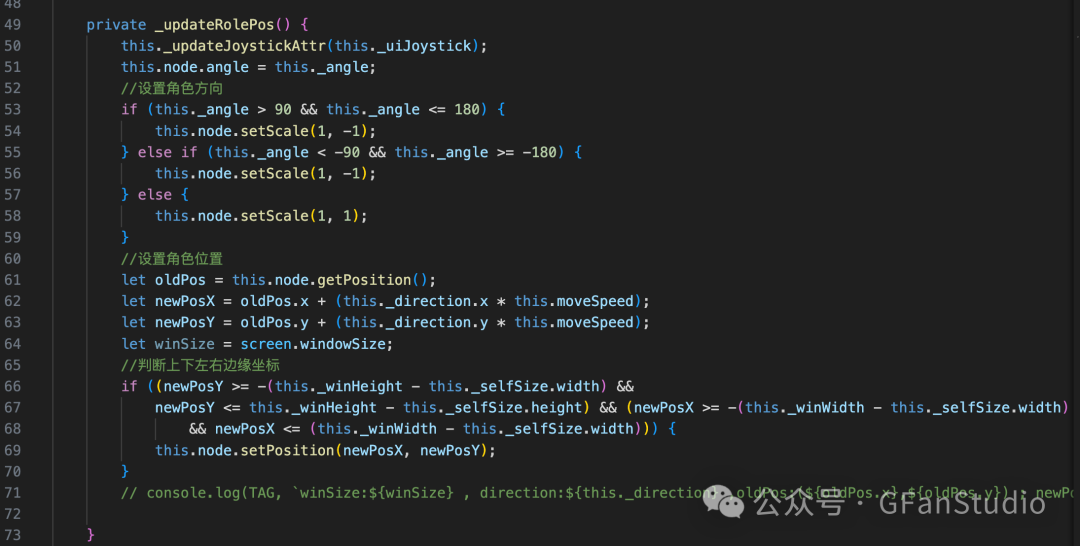
大致实现思路和逻辑就上面的,具体UI以及代码详细实现等细节逻辑可看具体游戏代码工程
<!!!文章末尾有完整代码下载链接地址!!!>
完整代码目录结构如下:


<!!!文章末尾有完整代码下载链接地址!!!>
详细实现代码工程逻辑请关注微信公众号GFanStudio回复 "虚拟摇杆" 即可获得项目工程下载地址;具体教学视频请关注B站Up主GFanStudio

另外QQ技术交流群交流学习2d/3d技术知识:1038743340
<!!!文章末尾有完整代码下载链接地址!!!>
游戏公司面试题-CocosCreator实现虚拟摇杆控制角色移动&中心旋转自转小球&割草旋转逻辑 完整代码下载地址如下:
虚拟摇杆控制角色移动&中心旋转自转小球&割草旋转逻辑Cocos商店地址
这篇关于游戏公司面试题系列-CocosCreator实现虚拟摇杆控制角色移动中心旋转自转小球割草旋转逻辑的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


