java算法day48 | 动态规划part09 ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III

本文主要是介绍java算法day48 | 动态规划part09 ● 198.打家劫舍 ● 213.打家劫舍II ● 337.打家劫舍III，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

198.打家劫舍

在这里插入图片描述

class Solution {public int rob(int[] nums) {if(nums.length==0) return 0;if(nums.length==1) return nums[0];int[] dp=new int[nums.length];dp[0]=nums[0];dp[1]=Math.max(nums[1],nums[0]);for(int i=2;i<nums.length;i++){dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i]);}return dp[nums.length-1];}
}

时间复杂度: O(n)
空间复杂度: O(n)

213.打家劫舍II

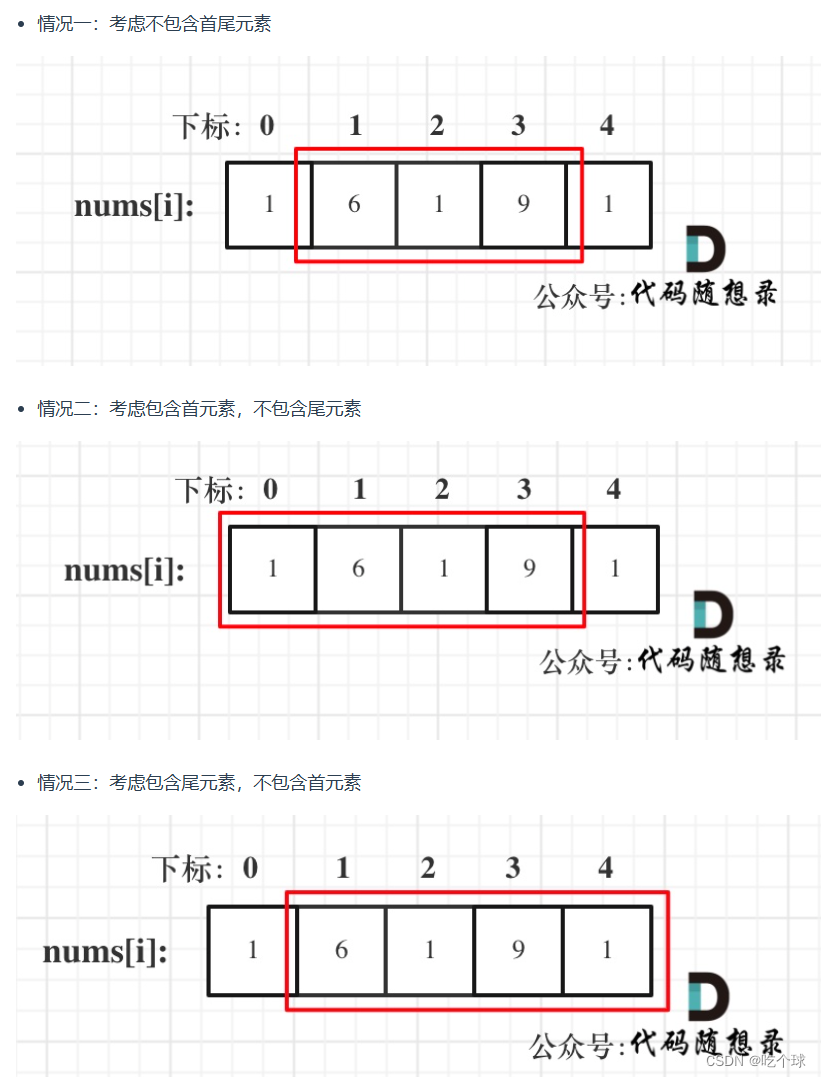
在这里插入图片描述

考虑以下三种情况，其中第一种情况包括在后面两种情况中。

class Solution {public int rob(int[] nums) {if(nums.length==0) return 0;if(nums.length==1) return nums[0];int rob1=robAction(nums,0,nums.length-1);int rob2=robAction(nums,1,nums.length);return Math.max(rob1,rob2);}public int robAction(int[] nums,int start,int end){if(end-start==1) return nums[start];int[] dp=new int[nums.length];dp[start]=nums[start];dp[start+1]=Math.max(nums[start],nums[start+1]);for(int i=start+2;i<end;i++){dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i]);}return dp[end-1];}
}

时间复杂度: O(n)
空间复杂度: O(n)

337.打家劫舍III

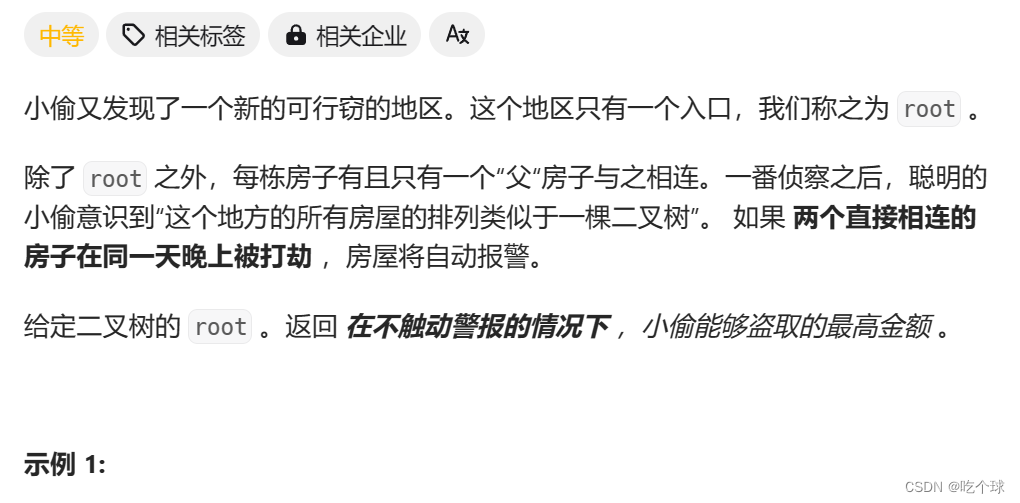
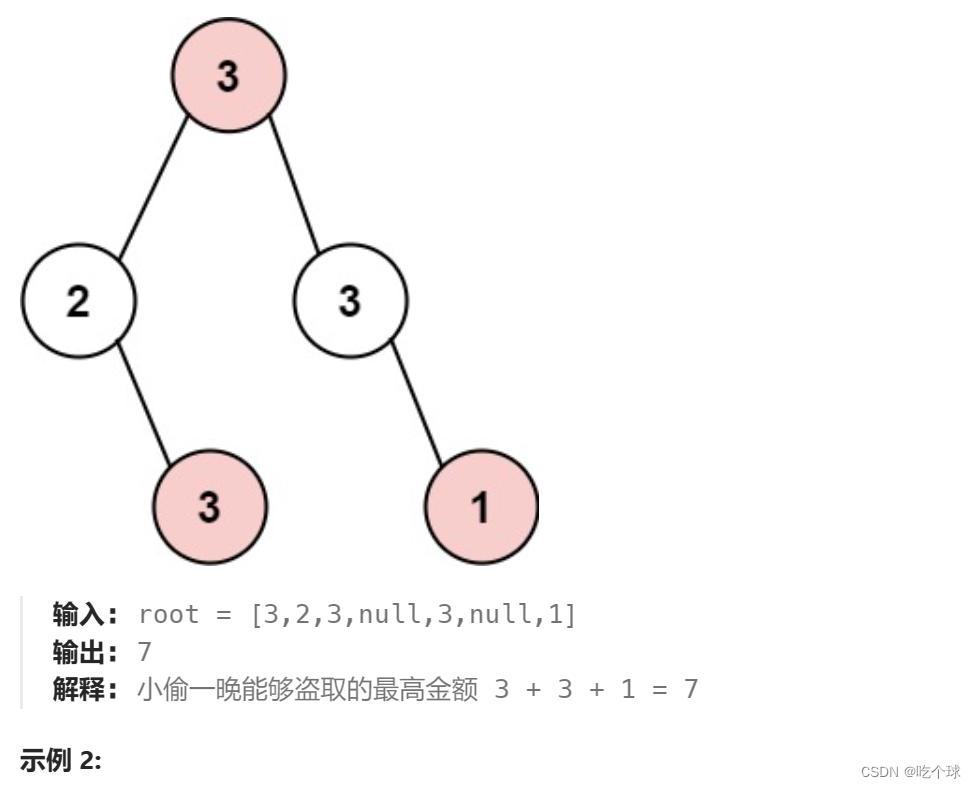
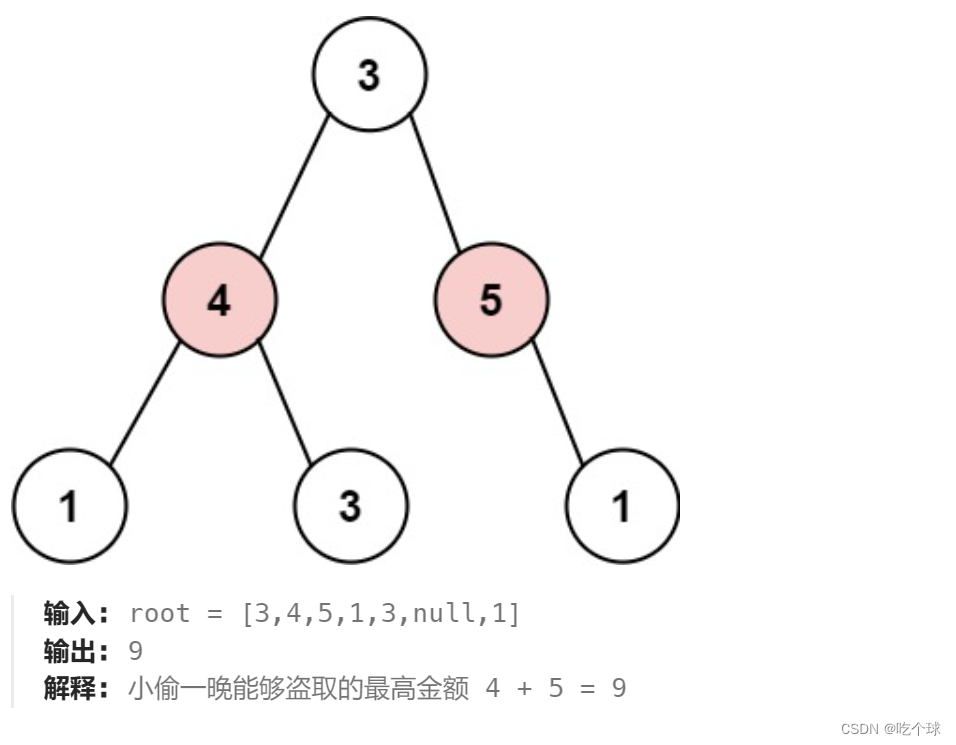
在这里插入图片描述

本题是树形dp的入门题目，一定要用后序遍历，建议看视频理解一下：代码随想录教程

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int rob(TreeNode root) {int[] res=new int[2];res=robAction(root);return Math.max(res[0],res[1]);}public int[] robAction(TreeNode root){if(root==null) return (new int[]{0,0});int[] left=robAction(root.left);int[] right=robAction(root.right);int val0=Math.max(left[0],left[1])+Math.max(right[0],right[1]);//不偷rootint val1=left[0]+right[0]+root.val;return new int[]{val0,val1};}
}