摆动序列（力扣376）

本文主要是介绍摆动序列（力扣376），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

题目
前知
题解
- 一、思路
- 二、解题方法
- 三、Code
总结

在这里插入图片描述

题目

Problem: 376. 摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 摆动序列 。第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

例如，[1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值(6, -3, 5, -7, 3) 是正负交替出现的。
相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5]
不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

示例 1：

输入：nums = [1,7,4,9,2,5]
输出：6
解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

示例 2：

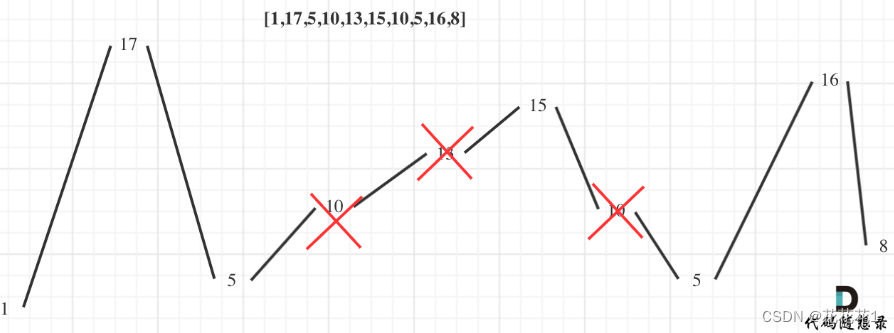
输入：nums = [1,17,5,10,13,15,10,5,16,8]
输出：7
解释：这个序列包含几个长度为 7 摆动序列。
其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

示例 3：

输入：nums = [1,2,3,4,5,6,7,8,9]
输出：2

前知

力扣（LeetCode）第376道题目是“摆动序列”（Wiggle Subsequence），属于动态规划和贪心算法的类型。这道题的要求是找到给定整数序列中最长的摆动子序列的长度。摆动序列是指相邻元素之间的差异在正负之间交替变化。

题解

一、思路

要想得到最大摆动序列的话，只要将单调坡上的结点删除，保留两端的结点，这个坡度就有两个峰值，是局部最优，由局部最优推出全局最优，由于题目只要求返回最大摆动序列的长度，用result变量统计，不用删除结点，用后一个值减去前一个值，得到前prediff后curdiff的值大小，如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 则可以确定存在峰值需要result++
，还有三种特殊情况在下面的解题方法还需要考虑一下

在这里插入图片描述

二、解题方法

本题大概代码是下面这样的：

//只有一个就返回摆动序列长度为1
if (nums.length <= 1) {return nums.length;
}
//计数
int result = 1;for (int i = 1; i < nums.length; i++) {//得到当前差值int curDiff = nums[i] - nums[i - 1];//如果当前差值和上一个差值为一正一负，出现波动就统计if ((prediff < 0 && curdiff > 0) || (prediff > 0 && curdiff < 0)) {result++;}preDiff = curDiff;
}
return count;

三种特殊情况：

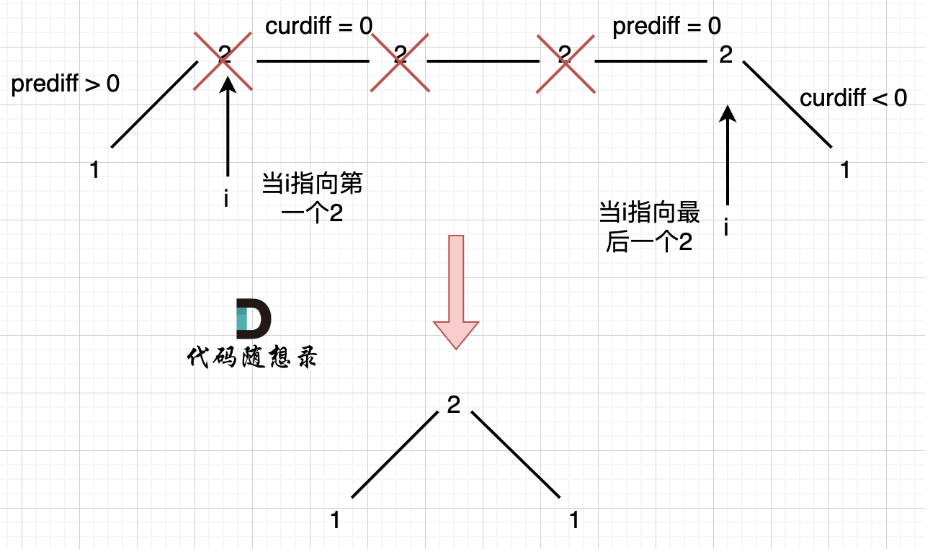
上下坡中有平坡：统一删除靠近左边平坡的点，到最后一个结点时的情况是prediff = 0 && curdiff < 0也要进行记录，所以左边的prediff都要加上与0判断相等的情况

if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0))

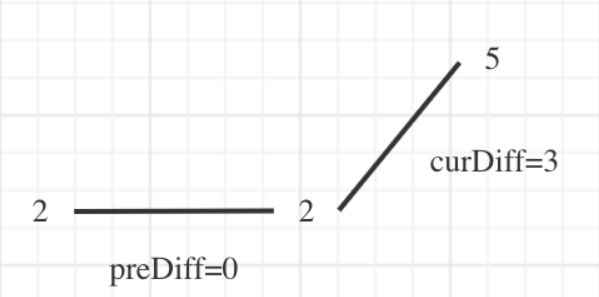
数组首尾两端：当数组只有两个结点时，无法计算出prediff与curdiff，让左边prediff初始为0，这样三个点会根据情况1自动删除左面的一个结点，统计result加1为2，result初始为1，因为nums数组至少都有一个元素，也就是摆动序列长度为1

//当前差值
int curDiff = 0;
//上一个差值
int preDiff = 0;

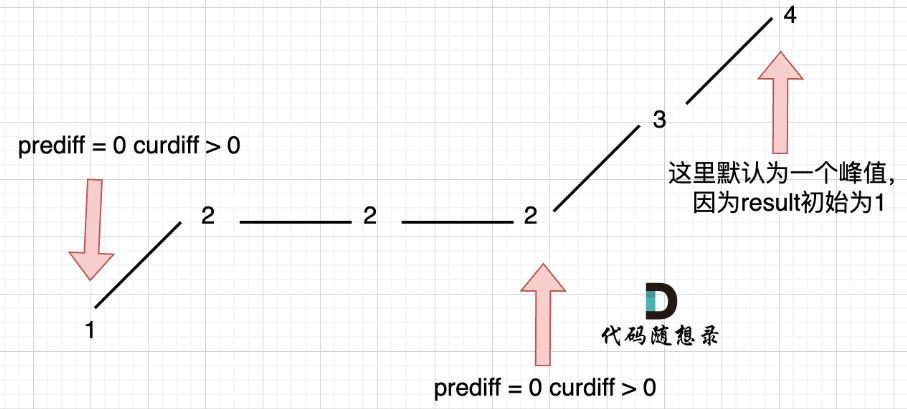
单调坡中有平坡：prediff不能每走一步都进行更新，要等出现波动时，再让prediff等于curdiff。
在下图中实际上只有数组首尾的1,4是摆动序列里的，result应该为2，但是在平坡的最后一个2的地方因为每走一步prediff都更新下一步的，所以在2的地方也计算了一个波动，只要把prediff更新操作放到if判断里面即可

if ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {count++;preDiff = curDiff;  // 注意这里，只在摆动变化的时候更新prediff
}

三、Code

class Solution {public int wiggleMaxLength(int[] nums) {if (nums.length <= 1) {return nums.length;}//当前差值int curDiff = 0;//上一个差值int preDiff = 0;int count = 1;for (int i = 1; i < nums.length; i++) {//得到当前差值curDiff = nums[i] - nums[i - 1];//如果当前差值和上一个差值为一正一负//等于0的情况表示初始时的preDiffif ((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {count++;preDiff = curDiff;}}return count;}
}