本文主要是介绍3.2-3.3 词法分析---NFA转换到DFA~DFA 最小化 Hopcroft 算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
子集构造算法:
因为NFA不适合直接用来做词法分析器的识别,是因为它的状态转移是不确定的,这种情况下写一个算法往往需要回溯,对于分析的效率影响会比较大,所以需要用子集构造算法由NFA将它转换成与它等价的DFA(因为DFA是确定有限状态自动机),最终转换成词法分析器可以使用的代码。
子集构造算法思想:
a(b|c)*
下图是一个NFA,很明显它的转移边包含 ε 所以它的状态转移是不确定的,我们所要做的是
由最开始的 NFA 状态出发,先读入任何一个字符看它能走到 NFA 的那个节点,并且考虑由于 ε 边的存在,实际上他能拓展走到那个边界上(走到这个边界,那么就没有任何的 ε 边能继续走下去),这个边界就是所有节点中的子集。(q0)
在这个边界上再读如任何的字符,可以走到那些节点,这些节点通过 ε 又可以走到那些集合,这样就会得到一个新的节点(q1)
现在可以想 这些节点(q2) 又可以走那些节点走到 ε 边界,得到一个集合…
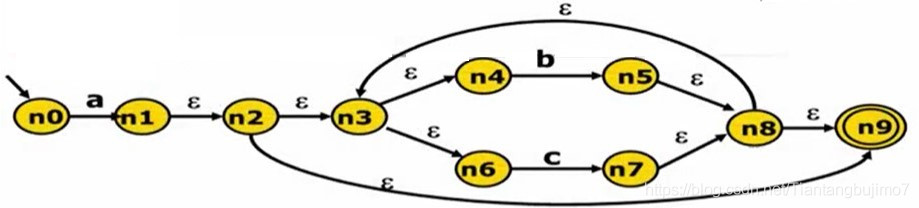
除了 a 可以走到的边之外,由于 ε 可以简化(它不消耗任何输入状态),所以我们转换 ε 边后它还可以走到后面的5个节点
— a —> n1
n0 — a —> {n1,n2,n3,n4,n6,n9}; 由 n0 读入 a 这个状态后所能走到的所有可能的状态 把这个集合记作 q0

在这个子集上,我们再读入 b,在这个子集中所有的状态上看b造成的转换
q1 — b —> n5
q1 — b —> {n5,n8,n9,n3,n4,n6} ;q1
那么按照以上逻辑及转换的节点:
q0 – a–> [q1] – b --> [q2] …
我们通过这样的构造过程就由 NFA 转换到DFA,因为转换后的结果就不会得到 ε 边了。
需要注意的是 q0 集合中,我们会到达接受状态 n9 ,q1 状态中我们也会最终到达接受状态所以这里 q1 和 q2 都是接受状态
q0 – a–> [[q1]] – b --> [[q2]] …
状态转换, 有一个子集 q1 ,q1在 字符 b 的驱动下可以转换成那些状态,这里实际有两个重要的操作。
1.先看原来的NFA,在所有的节点上b都能转换成那些状态,就能得到第一个集合,把他叫做 delta(q) ,
2.在这个集合上对每一个元素再求 ε 边界
对算法的讨论:
不动点算法:
算法为什么能够运行终止。 这个算法每循环一次,往工作表中增加元素的同时,还会向大Q增加元素,大Q里面的元素是 所有 NFA 状态集合的子集
Q = {{...} {...} ...}q0 q1
时间复杂度
最坏的情况 O(2n);
但在实际中不常发生,因为并不是每个子集都会出现
ε - 闭包的计算:深度优先

ε 闭包的计算 是通过 delta 转换后的三个节点边界,和(浅色)边界节点中的 ε 边 继续走还会到达那个节点,所有的这些节点加起来就会构造 ε 闭包 。
set closure = {} //全局变量 ε closure 这样一个闭包,他是一个集合,开始时初始化为空集//显然 对任何一个节点x计算一个 ε 闭包都将是一个集合
void sps_closure (x)closure += {x} //把 x 这个集合并到 closure 这个集合中去 是 U 操作,实际上在x的 ε 闭包上增加了一个元素它自身,任何节点的闭包首先包含它自身foreach (y:x --ε--> y) //对每个y元素做循环,y要满足条件 x 有一条 ε 指向 y,在有向图中 y 是x的后继节点,并且他们直接有效边上标的是 εif(!visited(y)) // 如果y还没有走过的话,那么递归的走y ,这是一个典型深度优先遍历算法eps_closure(y) 例子:
求 N1 的 ε 闭包
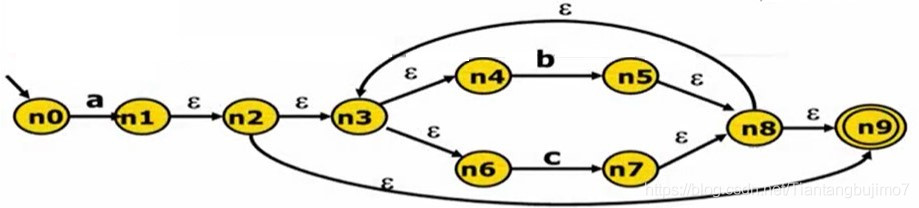
把 n1 加入到 ε closure 闭包中去
然后对于存在 ε 转换这样一条边的后继节点 n2 来说我再递归计算 n2,递归结束后 n2 会被加入到 closure 闭包中
然后递归 n3 … n9 这样
ε - 闭包的计算:宽度优先
它是基于队列的概念,就是它从q开始能够走到的后继所有的y 把他加到访问队列中访问队列不为空的时候就循环,不停按层序来遍历。
set closure = {};Q = []; //queue
void eps_closure(x) =
Q = [x];
while(Q not empty)q <- deQueue(Q)closure +=qforeach(y:q--ε -->y)if(!visited(y))enQueue(Q,y)
具体代码运作:
// 子集构造算法:工作表算法q0 <- eps_closure(n0) //起始状态是 n0 ,因为n0 上没有ε 边,所以 q0 = {n0}
Q <-{q0}; //此时 Q = {{n0}}
workList <- q0
while(workList != [])remove q from workList // q0 从 workList 中被移除foreach(character c) //对每一个字符做循环t <- e-closure (delta(q,c)) //循环的时候看 q上面对c的转换 q =0 ,当循环256 次到 c的时候才对它有转换 此时 delta(q0,'a') = {n1} //加上 ε{delta(q0,'a') = {n1}} ,就是算里面每一个元素的 delta 也就是 {n1,n2,n3,n4,n6,n9} 共6个不同的元素D[q,c] <- t //工作表中增加 q1,这里它还是只有一个元素,之前的元素 remove 掉了if(t\not\in Q)add t to Q and workList
计算结果:
起始状态 no q0 = {n0}
workList = q0
进图到 第七行 remove q from workList ,从 workList 移除 q0
然后 算 delta q1 = {n1,n2,n3,n4,n6,n9}D[q,c] <- t 就是 q0 --- a ---> q1
把 q1 加到 工作表 workList 中加入子集 workList q2
q1 delta b 转换子集 q2 = {n5,n8,n9,n3,n4,n6}
D[q,c] <- t q0 --- a ---> q1 --- b ---> q2加入子集 workList q3
q1 delta b 转换子集 q3 = {n7,n8,n9,n3,n4,n6}
D[q,c] <- t q0 --- a ---> q1 --- c ---> q2--- b ---> [q2]/
[q0[ --- a ---> [q1] \ --- c ---> [q2]q2 读入一个b 会在 n4 状态上做转换,到n5 就是 -> {n5,n8,n9,n3,n4,n6} ,我们发现如果从q2 读入一个状态,那么它得到的结果
和q2 是相同的,那么它起始是自循环的一条边q3 读入一个c 也是一个自循环在q2 状态中 读入一个 c 会转换到 q3
在q3 状态中 读入一个 b 会回到 q2

这个 DFA 包含4个状态,其中 q0 是初始状态,q1,q2,q3 是接受状态,这些状态可以进行相互合并。
非接受状态和接受状态不能合并,如果同样是非接受状态,或者都是接受状态,那么就有可以合并。
q2 和 q3 如果用一个状态来合并

把 q1 和 q4 合并融合成一个节点

这样的有限状态自动机 DFA 最后做代码实现的话要变成内部的一个数据结构表示显然状态和边越少,它所占用的
资源和内存也就越少,有可能会提升算法效率,所以我们要来研究有限状态自动机最小化的算法怎么来做
Hopcroft 算法

// 基于等级类的思想
split(s) //s 是状态的集合foreach (character c) //对每一个字符c做循环256次if(c can split s) //如果c能够对这个集合做切分的话就把它切成t1..tksplit s into T1,...,Tk //这里我们可以看到 q1 q2是一组 是同类的,q3对a的转移到了s3也就是说 a 这个字符把集合s切成了2个子集//一个是q1,q2,一个是q3
hopcroft()split all nodes into N,A //一开始就把所有的节点切分成2个等价类,一个N非接受状态,一个A接受状态while(set is still changes) //继续把里面是子集再切分split(s)
Hopcroft 算法在实际中是如何工作的:
示例1:
a(b|c)*

根据 Hopcroft 的思想首先我们会切分2个集合出来
N: q0
A: q1,q2,q3
继续看每个集合还是不是能切分,首先N不用看了它是单元素集合,
b 和 c 都无法区分q1,q2,q3的不同性,所以我们把这三个节点可以合并成一个新节点q4
并且b和c 都是会在自身上做的状态转移,所以我们要加上一条回边

示例2:
fee|fie
f(ee|ie)

首先切分成2个初始的集合:
N: q0,q1,q2,q4
A q3,q5
循环到字符 e 的时候都转换到了集合 A,q0,q1接受e的话,e导致q2, 都在它内部
e:{q0,q1},{q2,q4}
集合e:{q0,q1},{q2,q4},{q3,q5}s A
q2,q4 都能接受e 并且他们的子集都到了 集合A,所以这个集合不能被划分了
q0,q1,假设q1 接受了e,就会进入集合 s (q2,q4) 中
所以就把这个集合进一步切分成 {q0},{q1}
集合e:{q0},{q1},{q2,q4},{q3,q5}s A
那么最终的自动机

这篇关于3.2-3.3 词法分析---NFA转换到DFA~DFA 最小化 Hopcroft 算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







