Stable Diffusion扩散模型【详解】小白也能看懂！！

本文主要是介绍Stable Diffusion扩散模型【详解】小白也能看懂！！，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

此文涉及公式推导，需要参考这篇文章： Stable Diffusion扩散模型推导公式的基础知识

1、Diffusion的整体过程

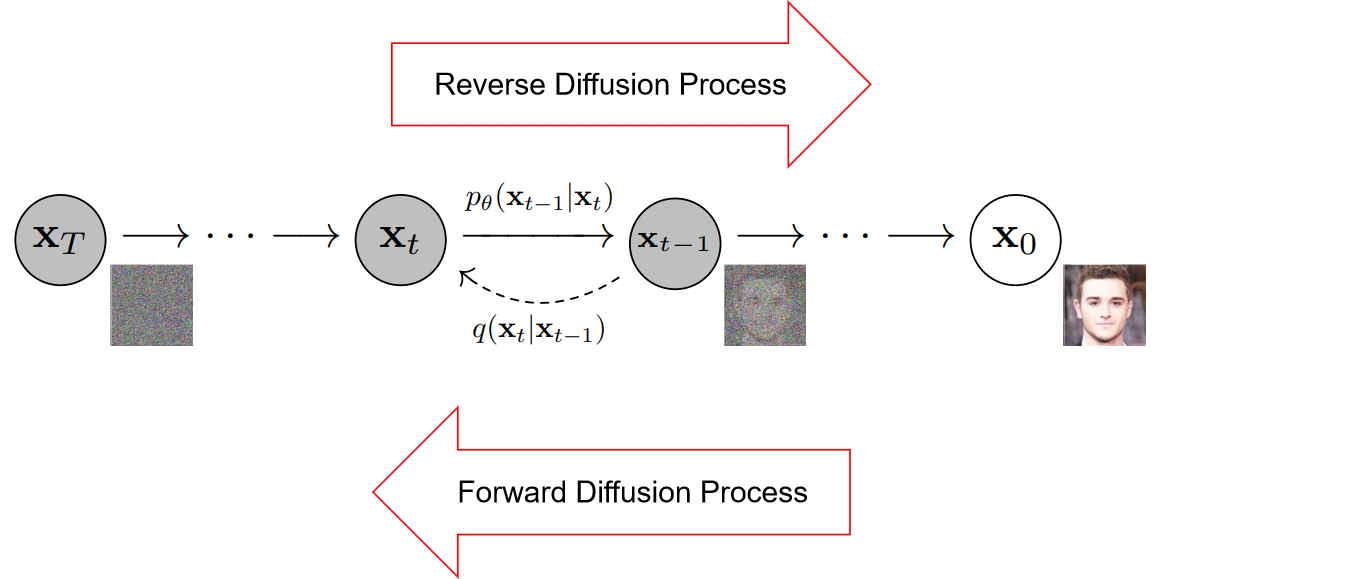
扩散过程是模拟图像加噪的逆向过程，也就是实现去噪的过程，
加噪是如下图从右到左的过程，称为反向扩散过程，
去噪是从左往右的过程，称为前向扩散过程，

2、加噪过程

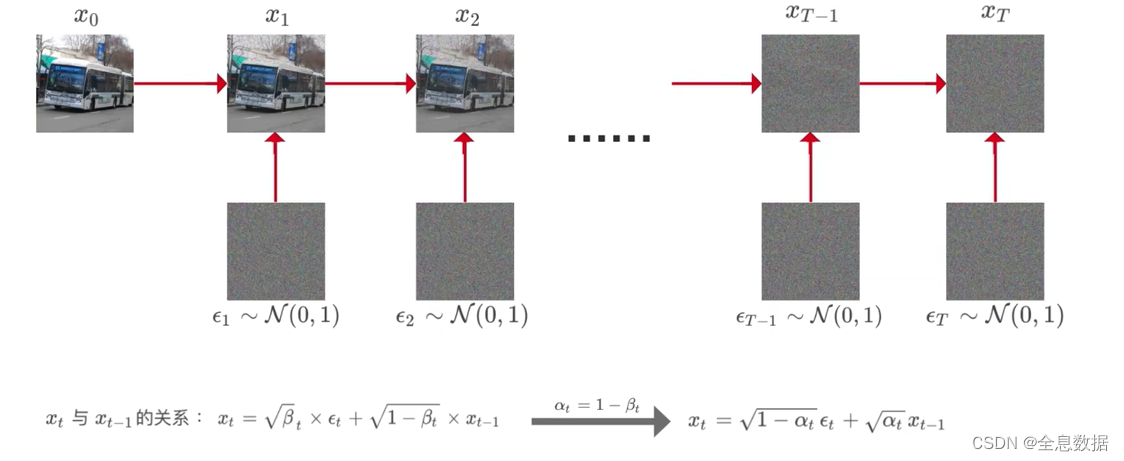
加噪过程如下图，下一时刻的图像是在上一时刻图像的基础上加入噪音生成的，
图中公式的含义：$x_t$表示 t 时刻的图像，${ϵ}_t$ 表示 t 时刻生成的随机分布的噪声图像，${\beta }_t$表示 t 时刻指定的常数，不同时刻的${\beta }_t$不同，随着时间 t 的递增而增加，但需要注意${\beta }_t$的值始终是比较小的，因为要让图像的数值占较大的比例，

2.1 加噪的具体细节

A、将图像$x$像素值映射到[-1,1]之间

图像加噪不是在原有图像上进行加噪的，而是通过把图片的每个像素的值转换为-1到1之间，比如像素的值是 $x$，则需要经过下面公式的处理$\frac{x}{255}\times 2-1$，转换到范围是-1到1之间，

代码：

def get_transform():class RescaleChannels(object):def __call__(self, sample):return 2 * sample - 1return torchvision.transforms.Compose([torchvision.transforms.ToTensor(), RescaleChannels()])

B、生成一张尺寸相同的噪声图片，像素值服从标准正态分布
$$ϵ\sim N(0,1)$$

x = {Tensor:(2, 3, 32, 32)}
noise = torch.randn_like(x)

C、$\alpha$和$\beta$
每个时刻的${\beta }_t$都各不相同，0 < ${\beta }_t$< 1，因为${\beta }_t$是作为权重存在的，且 ${\beta }_1<{\beta }_2<{\beta }_3<{\beta }_{T-1}<{\beta }_T$，

代码：

betas = generate_linear_schedule(args.num_timesteps,args.schedule_low * 1000 / args.num_timesteps,args.schedule_high * 1000 / args.num_timesteps)

$\beta$的取值代码，比如${\beta }_1$取值low，${\beta }_T$取值high，

# T:1000 Low/β1: 0.0001 high/βT: 0.02
def generate_linear_schedule(T, low, high):return np.linspace(low, high, T)

${\alpha }_t=1-{\beta }_t$，alphas = 1.0 - betas

alphas = 1.0 - betas
alphas_cumprod = np.cumprod(alphas)
to_torch = partial(torch.tensor, dtype=torch.float32)
self.registerbuffer("betas", totorch(betas))
self.registerbuffer("alphas", totorch(alphas))
self.register_buffer("alphas_cumprod", to_torch(alphas_cumprod))
self.register_buffer("sqrt_alphas_cumpnod", to_torch(np.sqrt(alphas_cumprod)))
self.register_buffer("sart_one_minus_alphas_cumprod", to_torch(np.sqrt(1 - alphas_cumprod)))
self.registerbuffer("reciprocal sart_alphas", totorch(np.sart(1 / alphas)))
self.register_buffer("remove_noise_coeff", to_torch(betas / np.sqrt(1 - alphas_cumprod)))
self.registerbuffer("siqma"，to_torch(np.sqrt(betas)))

D、任一时刻的图像$x_t$都可以由原图像$x_0$直接生成(可以由含$x_0$的公式直接表示)

$x_t$与$x_0$的关系：$x_t=\sqrt{1-\overline{{\alpha }_t}}ϵ+\sqrt{\overline{{\alpha }_t}}{x}_0$，${\alpha }_t=1-{\beta }_t$，$\overline{{\alpha }_t}={\alpha }_t{\alpha }_{t-1}...{\alpha }_2{\alpha }_1$

由上式可知，${\beta }_t$是常数，则${\alpha }_t$，$\sqrt{1-\overline{{\alpha }_t}}$，$\sqrt{\overline{{\alpha }_t}}$也是常数，$ϵ$也是已知的，所以可以直接由$x_0$生成$x_t$，

def perturb_x(self, x, t, noise):return (extract(self.sqrt_alphas_cumprod, t, x.shape) * x +extract(self.sqrt_one_minus_alphas_cumprod, t, x.shape) * noise)

def extract(a, t, x_shape):b, *_ = t.shapeout = a.gather(-1, t)return out.reshape(b, *((1,) * (len(x_shape) - 1)))

2.2 加噪过程的公式推导

加噪过程：

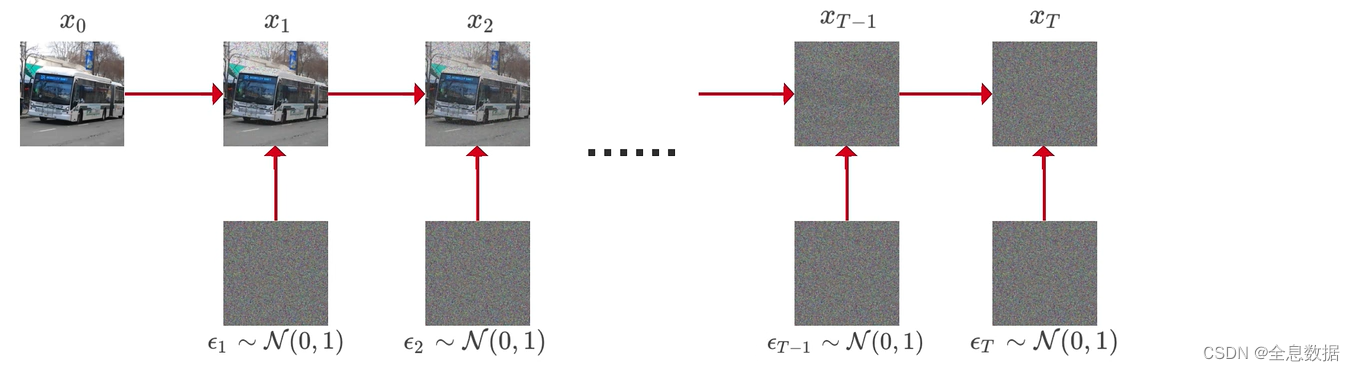
加噪过程的公式：

总结：

3、去噪过程

去噪是加噪的逆过程，由时间T时刻的图像逐渐去噪到时刻为0的图像，
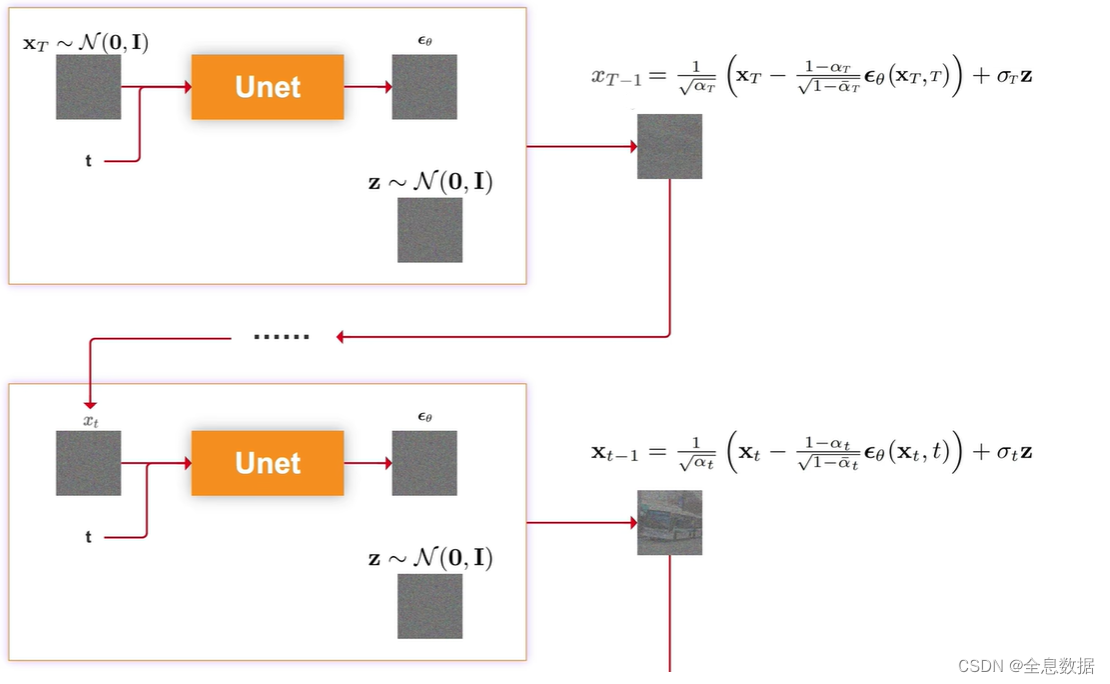
下面介绍一下由时刻为T的图像$x_T$去噪到时刻为T-1的图像$x_{T-1}$，输入为时刻为t的图像$x_t$和时刻t，喂给Unet网络生成${ϵ}_{\theta }$，其中$\theta$是Unet网络的所有参数，然后由下图中的${\mathbf{x}}_{t-1}$的公式即可生成时刻为t-1的图像${\mathbf{x}}_{t-1}$，

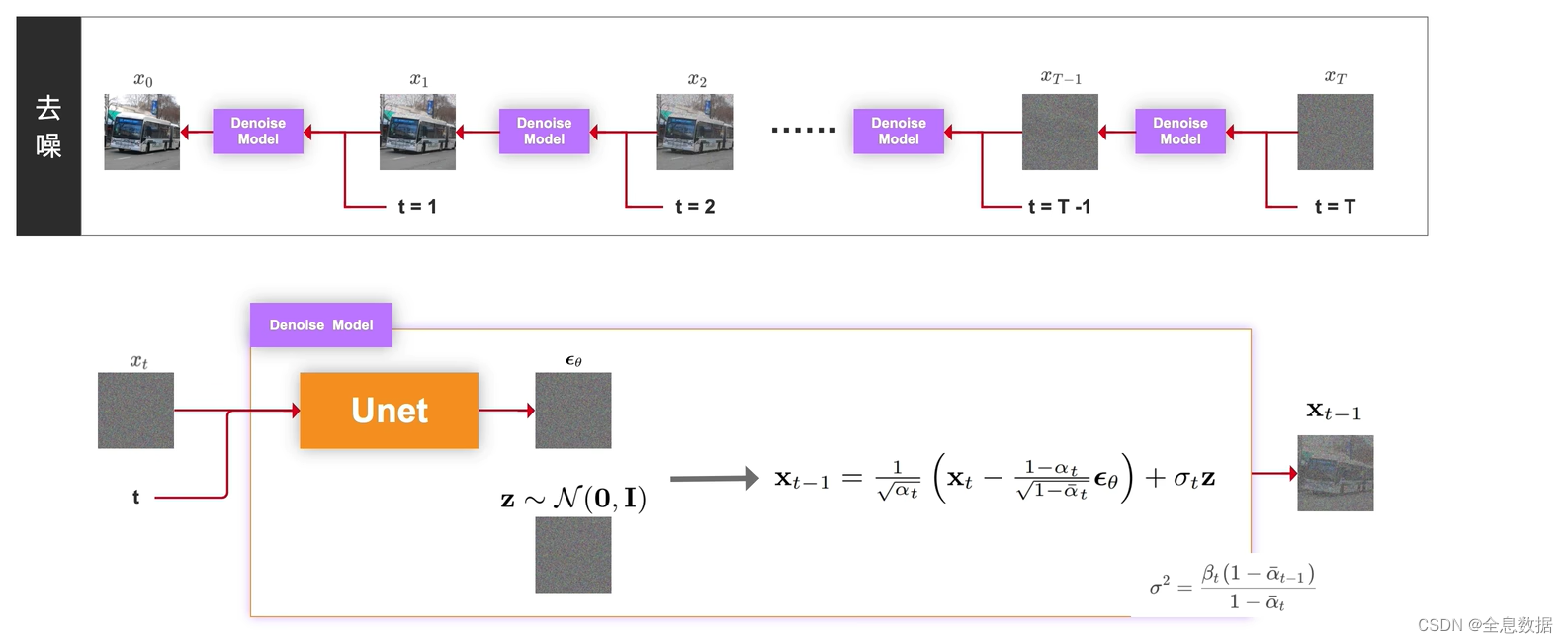
3.1 图像概率分布

去噪过程的2个假设:
(1)加噪过程看作马尔可夫链，假设去噪过程也是马尔可夫链，
(2)假设去噪过程是高斯分布，

假设数据集中有100张图片，每张图片的shape是4x4x3，假设每张图片的每个channel的每个像素点都服从正态分布，$x_{t-1}$的正态分布的均值 $\mu$ 和方差 ${\sigma }^2$ 只和$x_t$有关，已知在t时刻的图像，求t-1时刻的图像，

1、因为均值和方差$\mu (x_t)$，${\sigma }^2(x_t)$ 无法求出，所以我们决定让网络来帮我们预测均值和方差，
2、因为每一个像素都有自己的分布，都要预测出一个均值和方差，所以网络输出的尺寸需要和图像尺寸一致，所以我们选用 Unet 网络，
3、作者在论文中表示，方差并不会影响结果，所以网络只要预测均值就可以了，

4、损失函数

我们要求极大似然的最大值，需要对$\mu$和$\sigma$求导，但是对于扩散的过程是不可行的，如下面的公式无法求出，因为$x_1:x_T$的不同组合所求出的$x_0$的值也不同，
$$p(x_0)={\int }_{x_1:x_T}p(x_0|x_1:x_T)d_{x_1:x_T}$$

为了实现对极大似然函数的求导，把对极大似然求导的问题转换为ELBO :Evidence Lower Bound

对ELBO的公式继续进行化简，

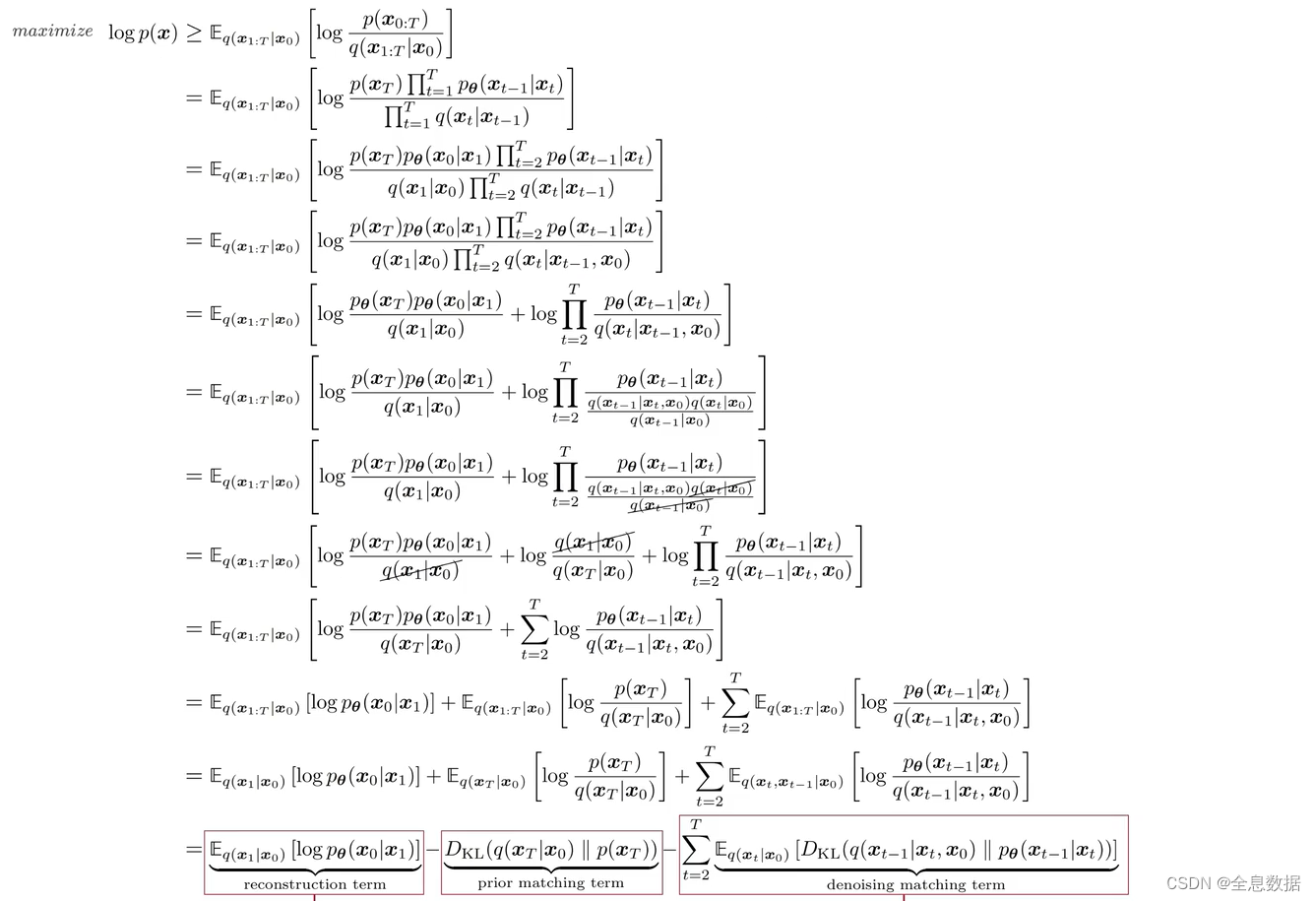
首先来看$q(x_{t-1}|x_t,x_0)$表示已知$x_0$和$x_t$的情况下推导$x_{t-1}$，这个公式是可以求解的，如上图公式推导；$p_{\theta }(x_{t-1}|x_t)$需要使用 Unet 预测出该分布的均值，

$q(x_{t-1}|x_t,x_0)$公式的推导如下：

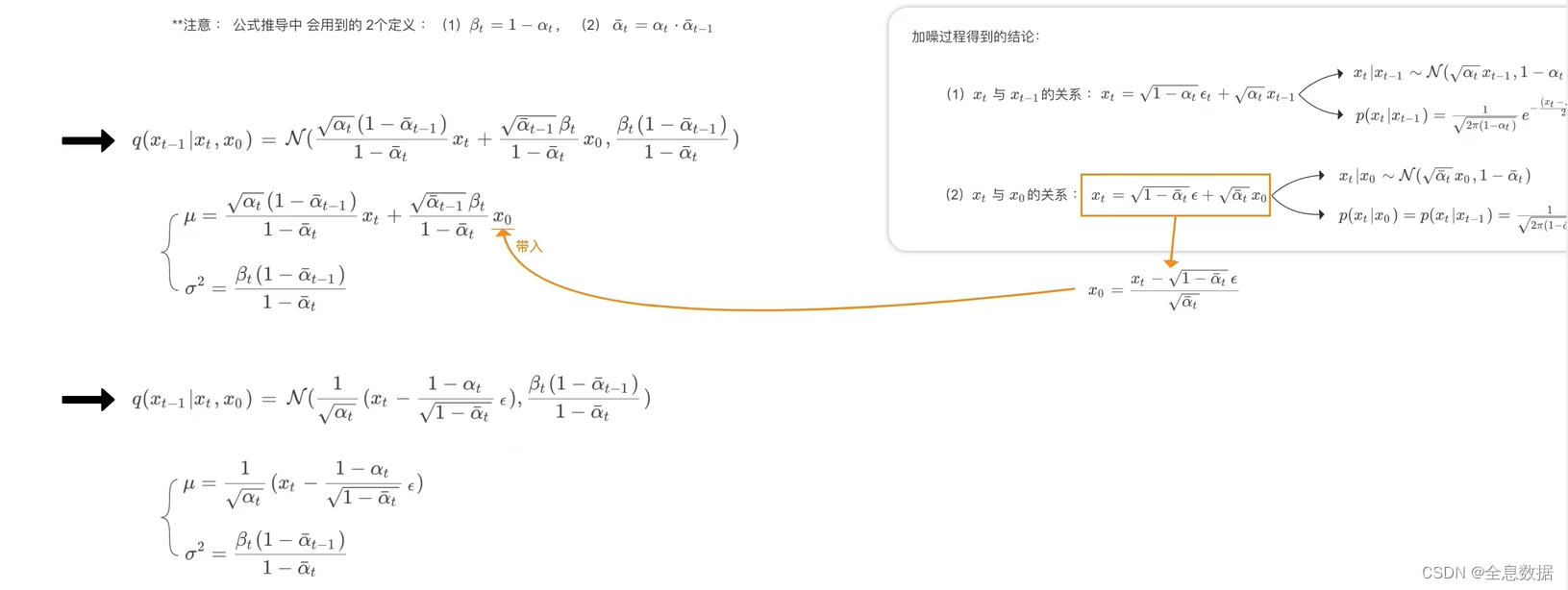
综上可知，UNet是在预测下面的公式，下面的公式中除了$ϵ$之外都是已知量，所以UNet网络实际预测的就是$ϵ$，

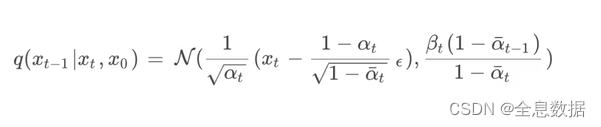
5、 伪代码过程

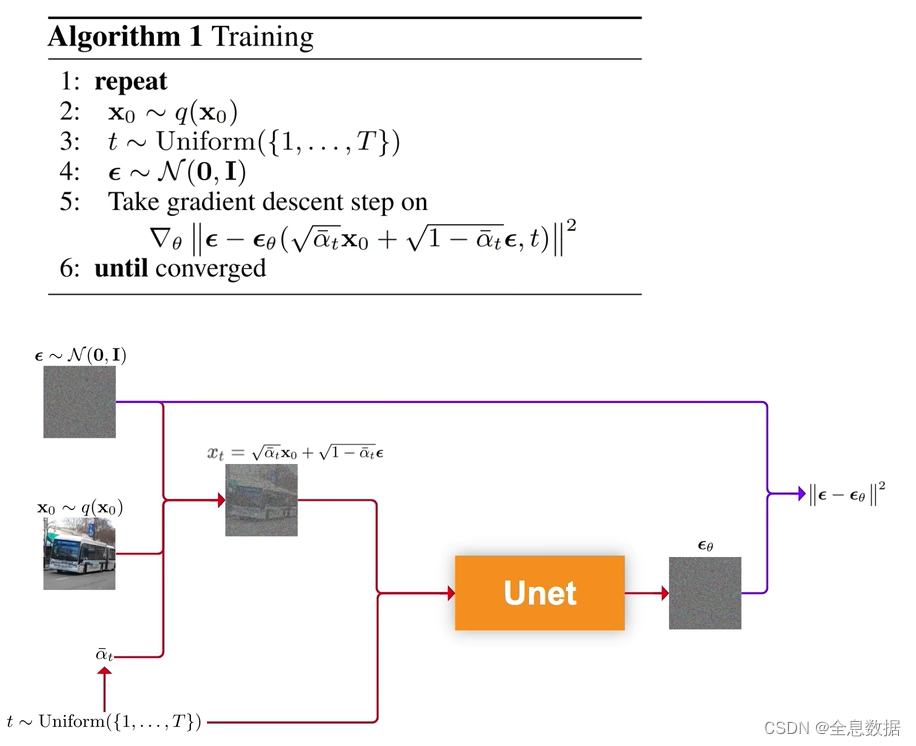
下图是训练阶段的伪代码，第1行和第6行表示第2行到第5行的代码一直在循环，
第2行：从数据集中筛选出一张图像，即为${\mathbf{x}}_0$,
第3行：从0到$T$的均匀分布中筛选出$t$，源码中$T$的范围设为1000，
第4行：从均值为0，方差为1的标准正态分布中采样出$ϵ$，$ϵ$的size和${\mathbf{x}}_0$的size是相同的，
第5行：$x_t$和从0到$T$的均匀分布中筛选出$t$喂给Unet，输出${ϵ}_{\theta }$，和第4行代码采样出的$ϵ$，$||ϵ-{ϵ}_{\theta }(...)|{|}^2$的均方差作为损失函数，对这个损失函数求梯度进行参数更新，参数是Unet所有参数的集合$\theta$，

下图是推导/采样/生成图片阶段的伪代码，

第1行：从随机分布中采样一个${\mathbf{x}}_T$，
第2行：遍历从$T$到1，
第3行：从随机分布中采样一个$\mathbf{z}$，
第4行：已知$\mathbf{z}$、${\alpha }_t$、${\sigma }_t$，${ϵ}_{\theta }$是Unet网络生成的，就可以得到${\mathbf{x}}_{t-1}$
循环2-4行代码，

---

参考：
1、CSDN链接：链接
2、哔哩视频：https://www.bilibili.com/video/BV1ju4y1x7L4/?p=5&spm_id_from=pageDriver
3、论文Denoising Diffusion Probabilistic Models：https://arxiv.org/pdf/2006.11239.pdf

这篇关于Stable Diffusion扩散模型【详解】小白也能看懂！！的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---