本文主要是介绍【C++进阶】AVL树(来自二叉搜索树的复仇),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

🪐🪐🪐欢迎来到程序员餐厅💫💫💫
主厨:邪王真眼
主厨的主页:Chef‘s blog
所属专栏:c++大冒险
总有光环在陨落,总有新星在闪烁
引言:
之前我们学习了二叉搜索树,有了它我们查找数据效率会很高,但是,有时候查找效率却很低
比如下面的情况:

我们称之为歪脖子树,可以看到他的搜索效率又退化到了O(N),为了解决这个问题,我们今天就来学习二叉搜索树plus——AVL树。
注:没有学习二叉搜索树的朋友建议先来看看这篇博客哦:
大战二叉搜索树
一.AVL树的概念
- 它的左右子树都是AVL树
- 左右子树高度之差(简称平衡因子)的绝对值不超过1
通过控制子树高度差,让AVL树几乎完美接近于平衡,便不会出现单支树的情况,保证了优良的搜索性能,因此AVL树又称为高度平衡二叉搜索树。
二. AVL树节点的模拟
template<class K,class V>
struct AVLNode
{AVLNode<K, V>*_left;// 该节点的左孩子AVLNode<K, V>*_right;// 该节点的右孩子AVLNode<K, V>* _parent;// 该节点的双亲pair<K, V> _val; // 该节点存储的数值int _bf;// 该节点的平衡因子(balance factor)AVLNode(pair<K,V> val=pair<K,V>()):_left(nullptr), _right(nullptr), (nullptr),_val(val)_bf(0);{}
};细节:
- 使用三叉链,分别是指向左节点,右节点和双亲节点
- 使用KV模型,数据存在于pair对象,而不是直接存在于节点
- 结点存储平衡因子,用来记录左右子树高度差(右树高度-左树高度)
三.AVL树模拟
3.1成员变量
template<class K,class V>
class AVLTree
{typedef AVLNode<K, V> Node;
public://函数
protected:AVLNode* _root;
};3.2 插入
因为AVL树也是二叉搜索树,所以默认成员函数和遍历与之前写的没什么不同,只是插入方式改变了(使得他能成为平衡树),所以这里重点讲解AVL树的插入。
3.2.1AVL树的插入过程可以分为两步:
- 1. 按照二叉搜索树的方式插入新节点
- 2. 调整节点的平衡因子
bool Insert(const pair<K, V>& val)
{if (_root == nullptr){_root = new Node(val);return true;}else{Node*cur=_root;Node*parent=nullptrwhile (cur){parent = cur;if (cur->_val > val)cur = cur->left;else if (cur->_val < val)cur = cur->_right;elsereturn false;}cur = new Node(val);if (parent->_val.first>cur->_val.first){parent->_left = cur;}else{parent->_parent = cur;}cur->_parent = parent;
//cur插入后,parent的平衡因子一定需要调整,在插入之前,parent
//的平衡因子分为三种情况:-1,0, 1while (parent)//向上回溯检测平衡因子{
//, 插入则分以下两种情况://1. 如果pCur插入到pParent的左侧,只需给pParent的平衡因子-1即可//2. 如果pCur插入到pParent的右侧,只需给pParent的平衡因子+1即可if (parent->_left == cur)parent->_bf--;elseparent->_bf++;
//此时:parent的平衡因子可能有三种情况:0,正负1, 正负2//1. 如果parent的平衡因子为0,说明插入之前parent的平衡因子为正负1,插入后被调整
//成0,此时满足AVL树的性质,插入成功,停止循环if (parent->_bf == 0)break;//平衡了,不用检测了
//2. 如果parent的平衡因子为正负1,说明插入前parent的平衡因子一定为0,插入后被更
//新成正负1,此时以parent为根的树的高度增加,需要继续向上更新else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}
// 3. 如果parent的平衡因子为正负2,则parent的平衡因子违反平衡树的性质,需要对其进
//行旋转处理else if (parent->_bf == 2 || parent->_bf == -2)//进行旋转{if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}}
//现在bf绝对值大于2,说明插入之前就已经不是AVL树结构,则直接断言报错elseassert(0);}}
}3.2.2 注意事项:
可能有老铁觉得bf绝对值为1时也符合AVL树结构,应该直接跳出循环,然而事实是:
- 1.这棵树现在bf绝对值是1说明之前是0,
- 2.他的父亲节点的bf可能因为他的bf改变而改变
- 3.或许他父亲原来bf就是1,在它的影响下就会变成2因此要一直回溯检验父亲,祖父........
3.2.3关于平衡因子的变动:
1.插入后bf为0

分析:
插入的节点插在了短的一边正好,消除了左右子树高度差
2.插入后bf为1或-1

分析:
此时增加了局部子树的高度,不确定有没有影响父亲的高度差,所以要向上回溯调查
四:旋转
4.1. 新节点插入较高左子树的左侧---左左:右单旋
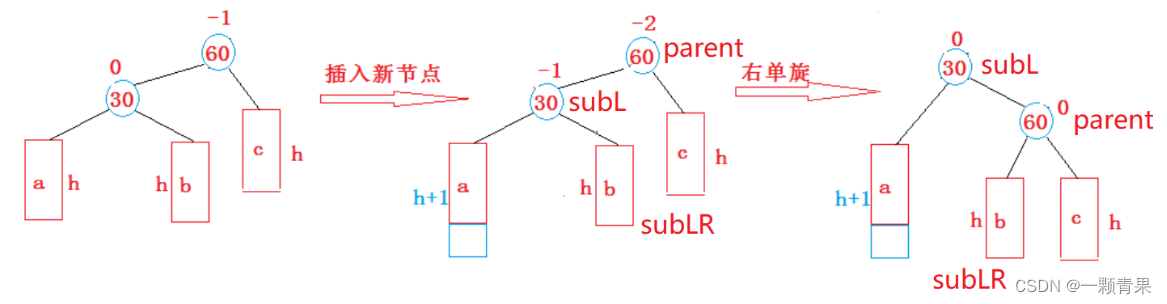
- 1. 30节点的右孩子可能存在,也可能不存在
- 2. 60可能是根节点,也可能是子树如果是根节点,旋转完成后,要更新根节点如果是子树,可能是某个节点的左子树,也可能是右子树
RotateR(AVLNode*parent)//右旋
{Node* grandparent = parent->_parent;Node* ChildL = parent->_left;if (grandparent){if (grandparent->_left == parent)grandparent->_left = ChildL;elsegrandparent->_right = ChildL;}else_root = ChildL;ChildL->_parent = grandparent;//两两一组进行改变parent->_left = ChildL->_right;ChildL->_right->_parent = parent;ChildL->_right = parent;parent->_parent = ChildL;//ChildL->_bf = parent->_bf = 0;
}4.2. 新节点插入较高右子树的右侧---右右:左单旋

情况与右旋类似,只要把修改对象ChildL和ChildL的右子树转化为ChildR和他的ChildR左子树即可
RotateL(AVLNode*parent)//左旋
{Node* grandparent = parent->_parent;Node* ChildR = parent->_right;if (grandparent){if (grandparent->_left == parent)grandparent->_left = ChildR;elsegrandparent->_right = ChildR;}else_root = ChildR;ChildR->_parent = grandparent;parent->_right = ChildR->_left;ChildR->_left->_parent = parent;ChildR->_left = parent;parent->_parent = ChildR;ChildR->_bf = parent->_bf = 0;
}4.3. 新节点插入较高右子树的左侧---右左:右左旋
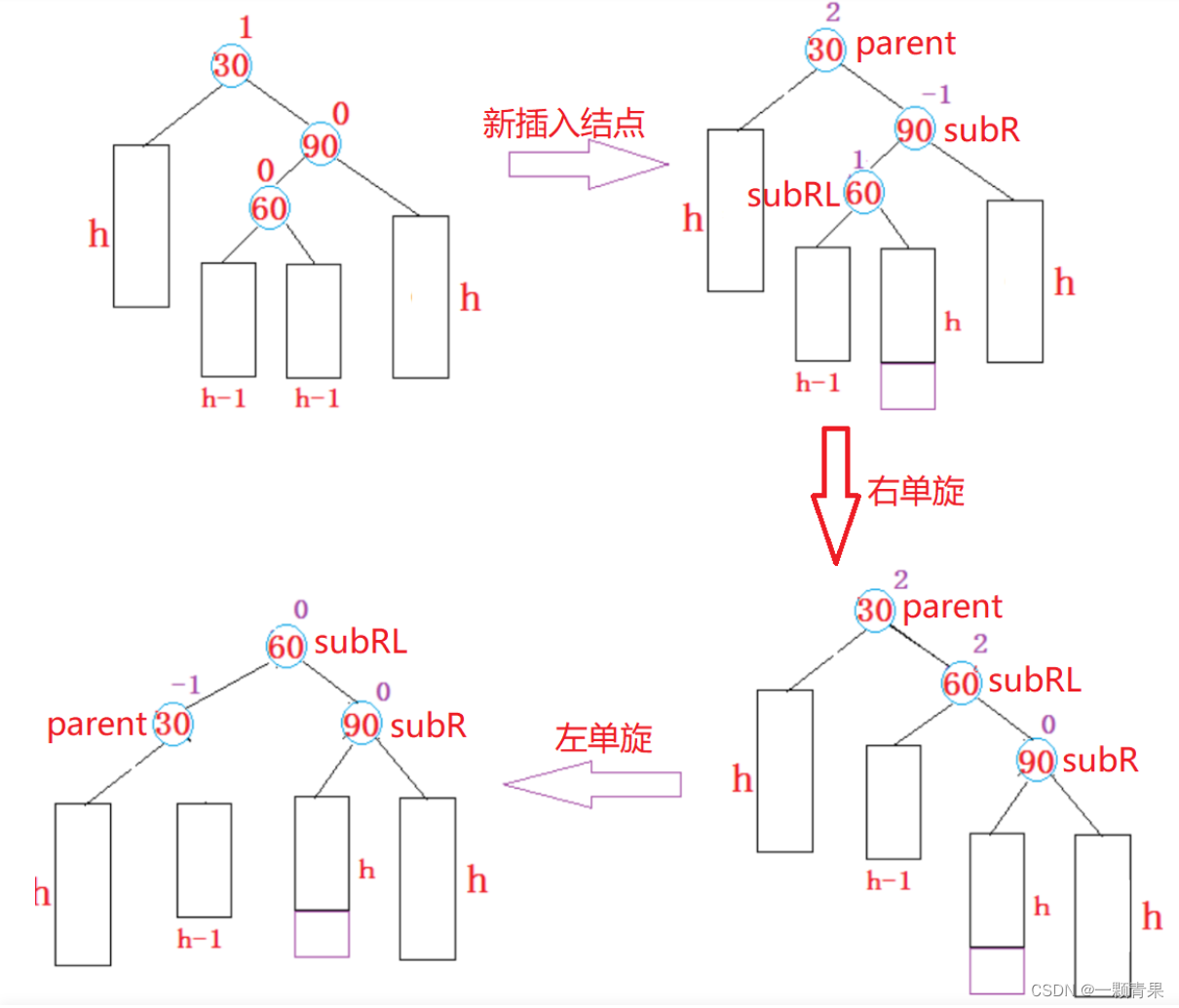
RotateRL(AVLNode*parent)//双旋,先右旋在左旋
{Node* ChildR = parent->_right;int bf = ChildR->_left->_bf;RotateR(ChildR);RotateL(parent);if (bf == 0){parent->_bf = 0;ChildR->_bf = 0;ChildR->_left->_bf = 0;}else if (bf == 1){parent->_bf = -1;ChildR->_bf = 0;ChildR->_left->_bf = 0;}else if (bf == -1){parent->_bf = 0;ChildR->_left->_bf = 0;ChildR->_bf = 1;}else{assert(false);}
}4.4. 新节点插入较高左子树的右侧---左右:左右旋
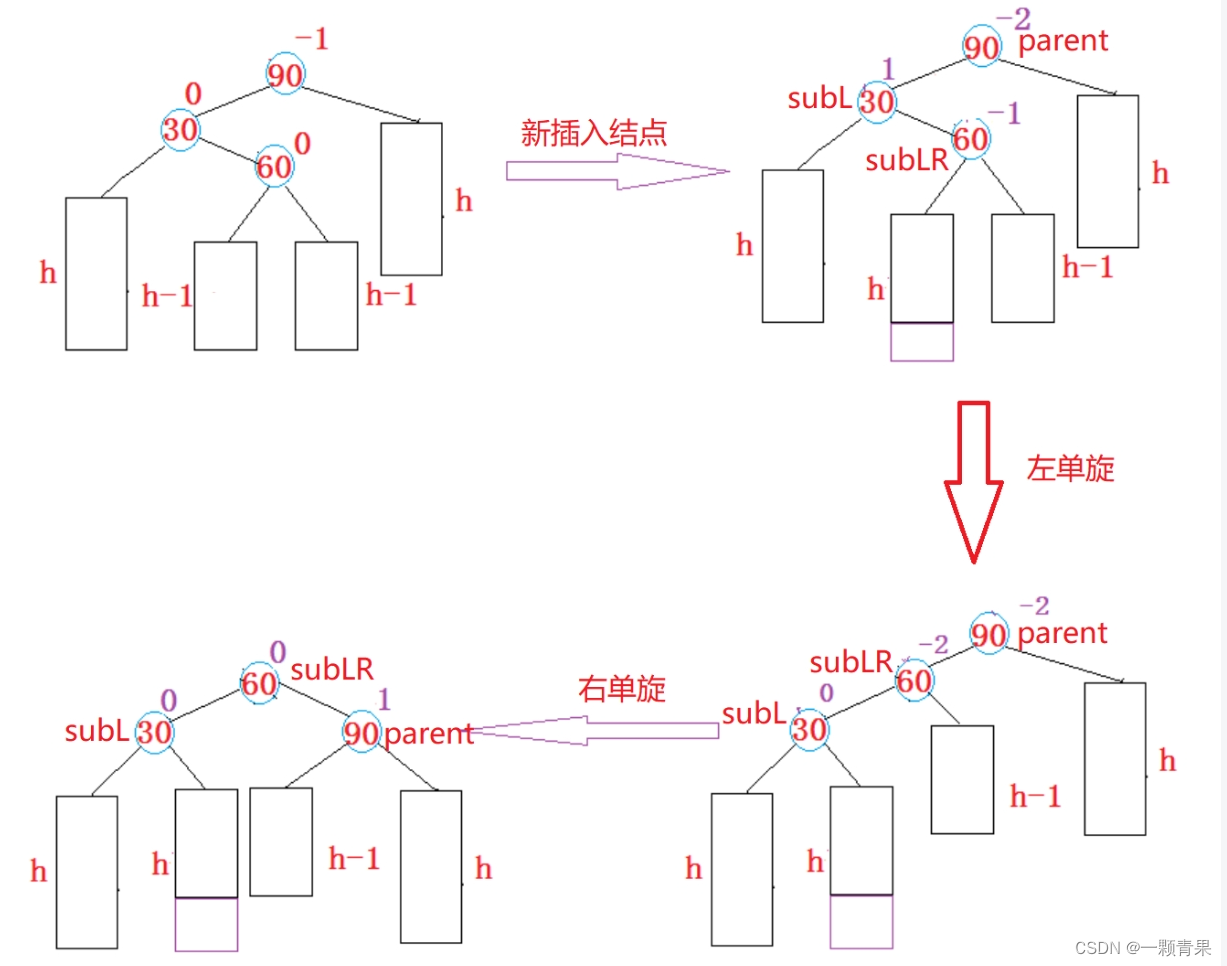
RotateLR(AVLNode*parent)//双旋,先左旋,再右旋
{Node* ChildL = parent->_left;int bf = ChildL->_right->_bf;RotateR(ChildL);RotateL(parent);if (bf == 0){parent->_bf = 0;ChildL->_bf = 0;ChildL->_right->_bf = 0;}else if (bf == 1){parent->_bf = 0;ChildL->_bf = -1;ChildL->_right->_bf = 0;}else if (bf == -1){parent->_bf = 1;ChildL->_right->_bf = 0;ChildL->_bf = 0;}else{assert(false);}
}旋转总结:
- 1. pParent的平衡因子为2,说明pParent的右子树高,设pParent的右子树的根为pSubR 当pSubR的平衡因子为1时,执行左单旋当pSubR的平衡因子为-1时,执行右左双旋
- 2. pParent的平衡因子为-2,说明pParent的左子树高,设pParent的左子树的根为pSubL 当pSubL的平衡因子为-1是,执行右单旋 当pSubL的平衡因子为1时,执行左右双旋旋转完成后,原pParent为根的子树个高度降低,已经平衡,不需要再向上更新。
5 AVL树的验证
5.1. 验证其为二叉5.搜索树
void Inorde(Node* root,vector<pair<K,V>>&v){if (root == nullptr)return;Inorde(root->_left, v);v.push_back(root->_val);Inorde(root->_right, v);}5.2. 验证其为平衡树
- 每个节点子树高度差的绝对值不超过1
- 节点的平衡因子是否计算正确
int high(Node* root)
{if (root == nullptr)return 0;int left = high(root->left);int right = high(root->right);int x = left > right ? left : right;return 1 + x;
}
bool _IsBalanceTree(Node* pRoot)
{// 空树也是AVL树if (nullptr == pRoot) return true;// 计算pRoot节点的平衡因子:即pRoot左右子树的高度差int leftHeight = _Height(pRoot->_pLeft);int rightHeight = _Height(pRoot->_pRight);int diff = rightHeight - leftHeight;
// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者// pRoot平衡因子的绝对值超过1,则一定不是AVL树if (diff != pRoot->_bf || (diff > 1 || diff < -1))return false;// pRoot的左和右如果都是AVL树,则该树一定是AVL树return _IsBalanceTree(pRoot->_pLeft) && _IsBalanceTree(pRoot-
>_pRight);}6. AVL树的性能
6.1优势:
6.2劣势:
结语:

这篇关于【C++进阶】AVL树(来自二叉搜索树的复仇)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






