本文主要是介绍代码随想录算法训练营Day42|LC416 分割等和子集,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一句话总结:背包问题。
原题链接:416 分割等和子集
拿到题先明确这是动态规划的题,具体类型是01背包问题。到了题目解法这里,首先判断数组加和是否为偶数,否则return false。然后就是01背包问题的解题思路了。具体地,将target设置为sum / 2,即背包的容量就是sum / 2,然后背包中放进来的商品价值与所占体积均为nums[i],每个nums[i]仅能加入答案一次。最后判断一下dp[target] == target即可。
接下来分析一下背包问题的思路。
动规五部曲分析如下:
-
确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
本题中每一个元素的数值既是重量,也是价值。
套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
也有背包装不满的时候,拿输入数组 [1, 5, 11, 5]举例, dp[7] 只能等于 6,因为 只能放进 1 和 5。
而dp[6] 就可以等于6了,放进1 和 5,那么dp[6] == 6,说明背包装满了。
-
确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
-
dp数组的初始化
从dp[j]的定义来看,首先dp[0]一定是0。
如果题目给的价值都是正整数,那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷,这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
由于本题题目中只包含正整数的非空数组,所以非0下标的元素初始化为0即可。
-
确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
代码如下:
// 开始 01背包
for(int i = 0; i < nums.length; i++) {for(int j = target; j >= nums[i]; j--) { // 每一个元素一定是不可重复放入,所以从大到小遍历dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}
}-
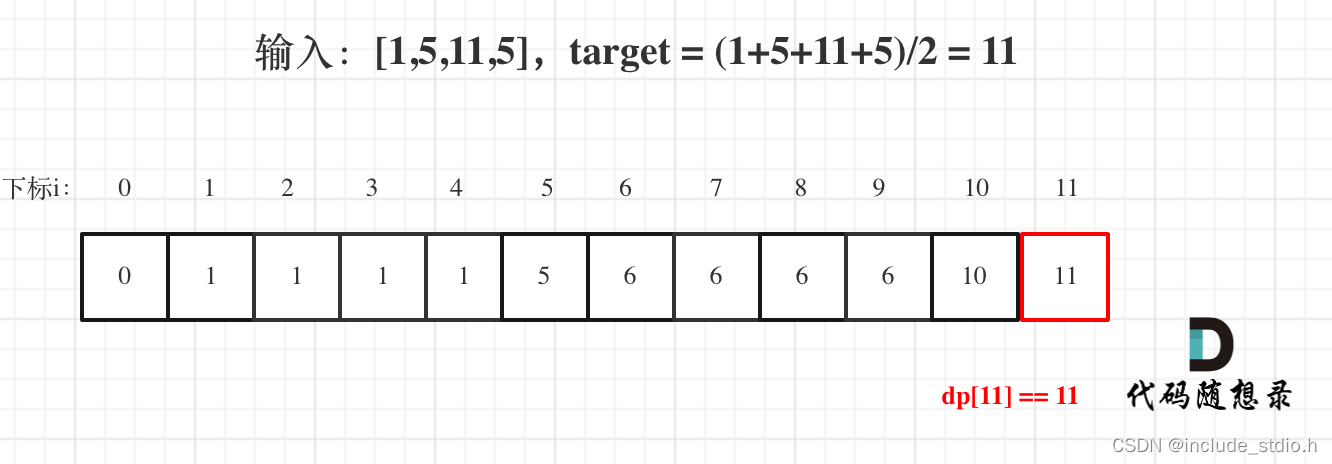
举例推导dp数组
首先需要明确的是dp[j]的数值一定是小于等于j的。然后手算过程如图:
以上五部曲来源:链接。
public class Solution {public boolean canPartition(int[] nums) {int n = nums.length;int sum = 0;for (int x : nums) {sum += x;}if ((sum & 1) == 1) {return false;}int target = sum / 2;int[] dp = new int[target + 1];for (int i = 1; i < n; ++i) {for (int j = target; j >= nums[i]; --j) {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}if (dp[target] == target) return true;}return dp[target] == target;}
}这篇关于代码随想录算法训练营Day42|LC416 分割等和子集的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




