本文主要是介绍数据结构刷题篇 之 【力扣二叉树基础OJ】详细讲解(含每道题链接及递归图解),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
 有没有一起拼用银行卡的,取钱的时候我用,存钱的时候你用
有没有一起拼用银行卡的,取钱的时候我用,存钱的时候你用
1、相同的树
难度等级:⭐
直达链接:相同的树
2、单值二叉树
难度等级:⭐
直达链接:单值二叉树
3、对称二叉树
难度等级:⭐⭐
直达链接:对称二叉树
4、二叉树的前序遍历
难度等级:⭐⭐⭐
直达链接:二叉树的前序遍历
5、另一颗树的子树
难度等级:⭐⭐⭐⭐
直达链接:另一颗子树
–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀-正文开始-❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–❀–
1、相同的树
直达链接:相同的树
题目:
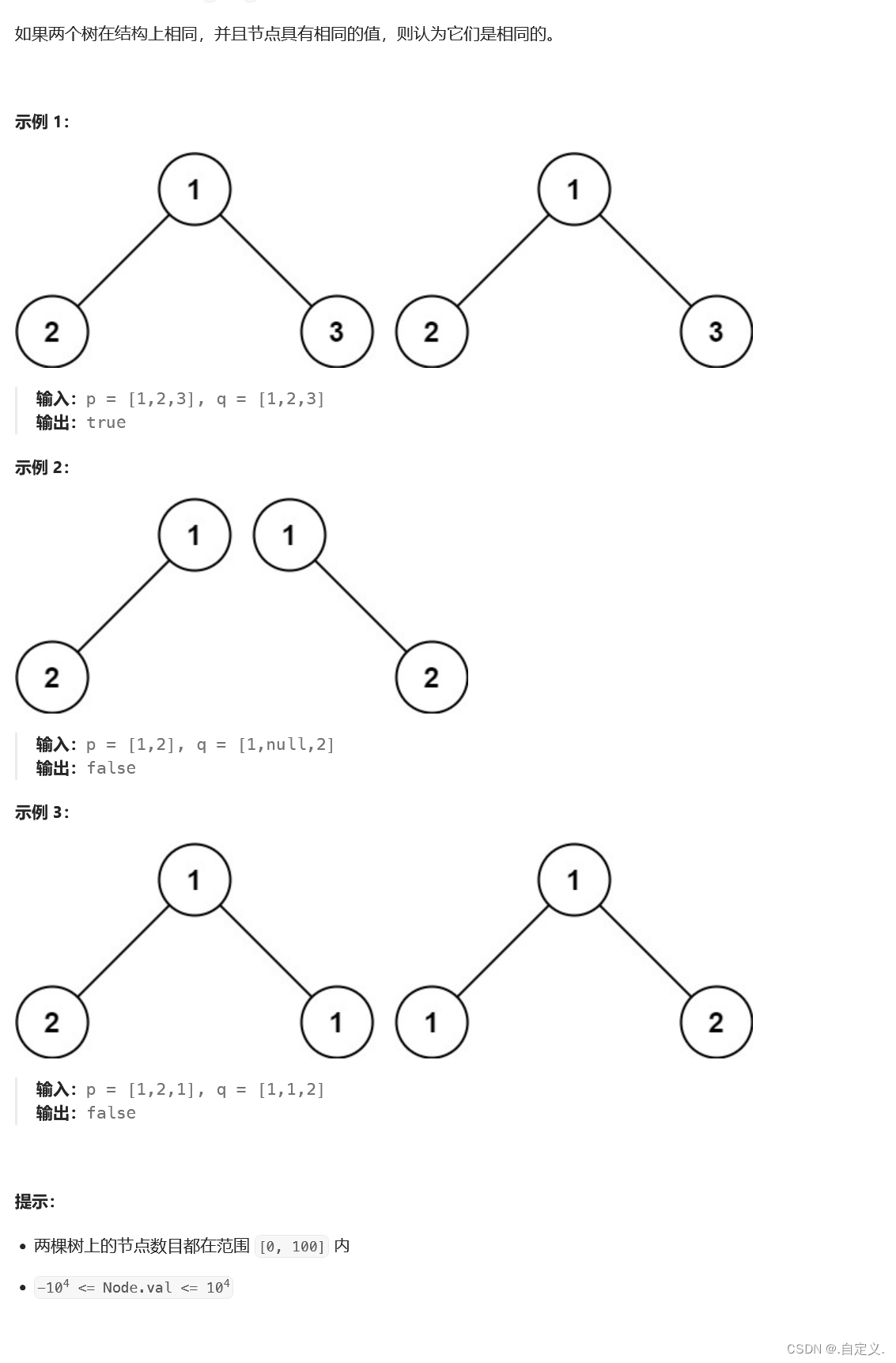 解题思路:
解题思路:
判断两个二叉树是否相同,而二叉树又分为根和左右子二叉树,左右子二叉树也可以再分(有的话),即需要判断根是否相同,相同再继续比较左右子树,比较左右子树也是需要判断根是否相同,相同的话继续向下比较,这就比较适合用递归来进行解题。
那么下面我们就需要找最小子问题,也就是判断递归终止的条件,这里我们需要考虑到空指针的问题
1.传过来的两个形参可能都是空指针,那么直接返回true
2.而也可能有一个为空,那么就返回false
3.两个都不为空比较数值是否相等即可
解题代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//两个指针都为空if(p == NULL && q == NULL){return true;}//其中有一个为空if(p == NULL || q == NULL){return false;}//两个指针都不为空if(p->val != q->val){return false;}return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}
这里以下面两个二叉树给大家进行代码递归图解,其他的大家可以自行动手,有利于加深理解
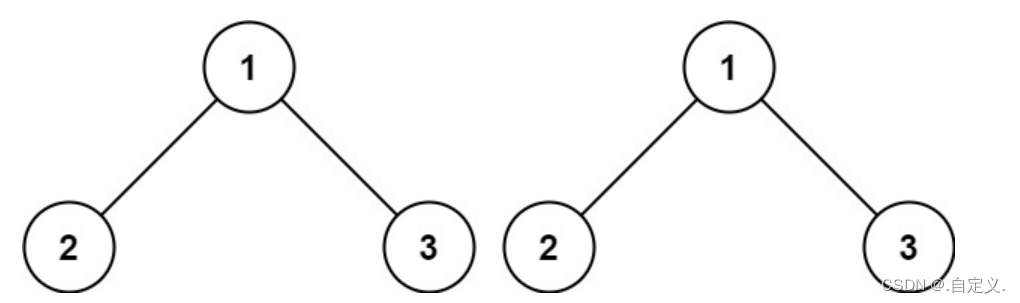 代码递归图解:
代码递归图解:

2、单值二叉树
直达链接:单值二叉树
题目:
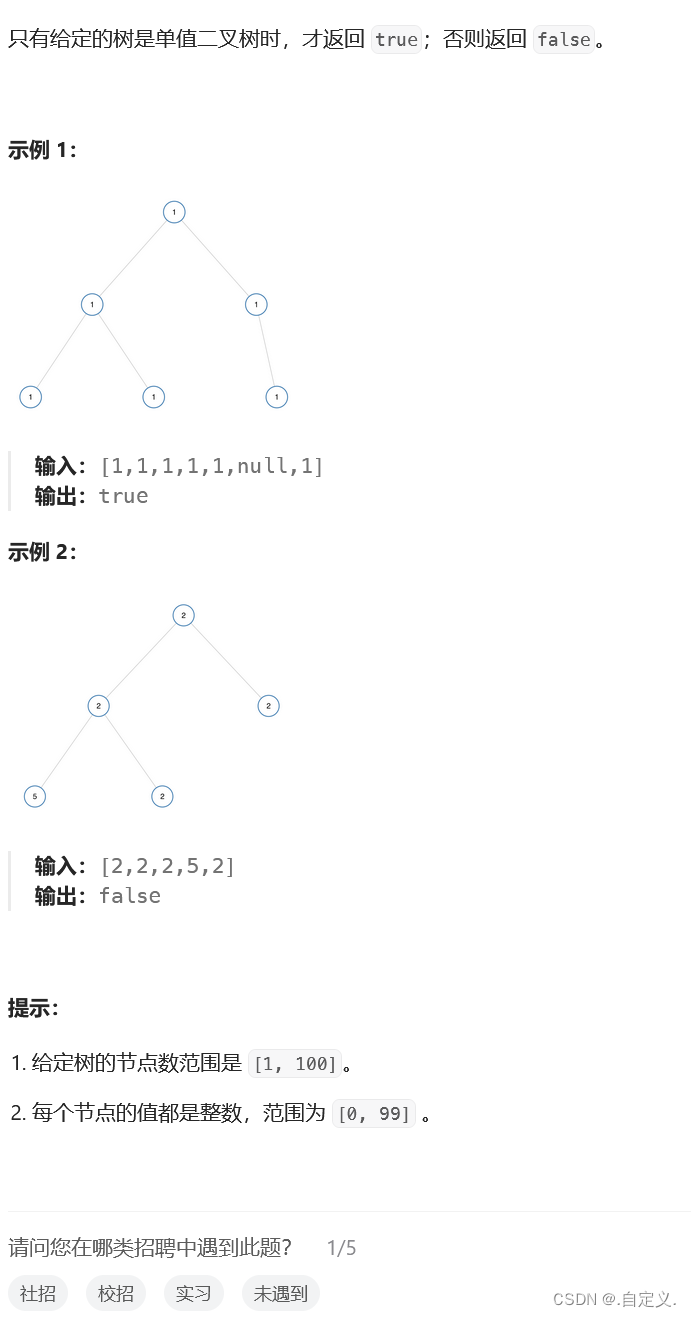 解题思路:
解题思路:
这道题并不难,还是依照老套路进行递归遍历,比较根和子节点的值,不相等就返回false,相等就继续想向下进行递归(有的话),再比较根和子节点。。。
那么我们还需要考虑一个递归最小子问题,所传的形参为空指针的情况,形参为空指针也分两种情况:
1.开始所传的就是空指针
2.递归到叶节点的子节点
这两种情况都直接返回true即可。
解题代码:
bool isUnivalTree(struct TreeNode* root) {//根为空if(root == NULL){return true;}//根不为空if(root->left && root->val != root->left->val){return false;}if(root->right && root->val != root->right->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}
我们以下面二叉树举例进行递归图解:
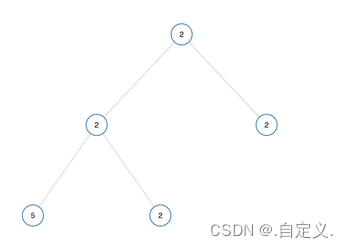
代码递归图解:
 方块表示调用该函数在内存上所开辟的空间,圆表示访问子节点的数值。
方块表示调用该函数在内存上所开辟的空间,圆表示访问子节点的数值。
3、对称二叉树
直达链接:对称二叉树
题目:
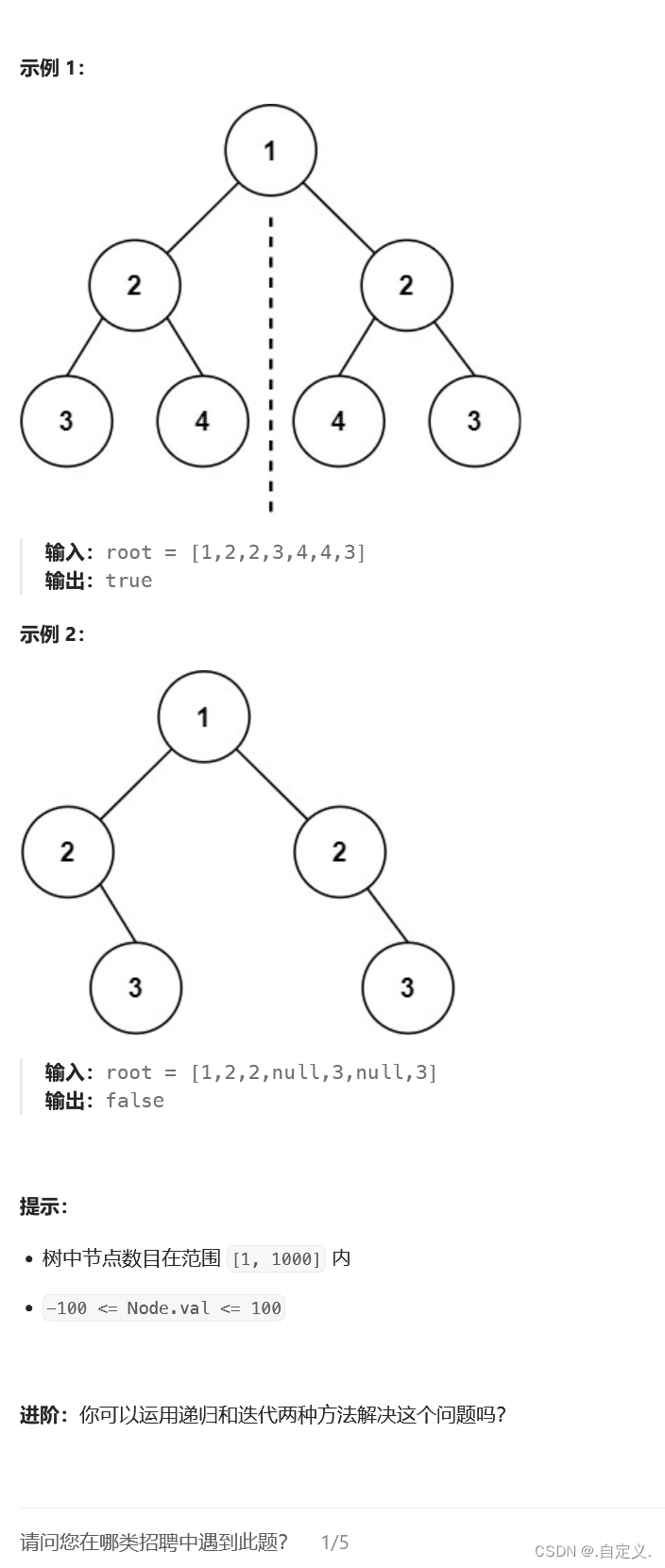 解题思路:
解题思路:
这道OJ题读完题目再看所给的函数接口大家可能就一头雾水了。
函数中所传的形参只有一个二叉树的指针。
而我们要进行对称判断的话是必须左右子树同时进行递归到相应位置节点判断节点是否相等。
这就有点难办了,同学可以先思考如何进行解决
假如已经进入到二叉树的两个子树判断,这里就和判断相同二叉树一样了
1.两个根节点都为空返回true
2.只有一个为空返回false
3.都不为空判断是否相等
解题代码:
bool is_Symmetric(struct TreeNode* left,struct TreeNode* right)
{//为空情况if(left == NULL && right == NULL){return true;}if(left == NULL || right == NULL){return false;}//不为空if(left->val != right->val){return false;}return is_Symmetric(left->left,right->right) && is_Symmetric(left->right,right->left);
}bool isSymmetric(struct TreeNode* root) {return is_Symmetric(root->left,root->right);
}
看到代码想必大家已经恍然大悟了
我们可以再创造一个函数将root的左右节点作为实参进行传递,这样就解决只有一个根节点指针的问题了
到is_Symmetric函数中实现逻辑与上面题相同的树就一样了,这里就不再进行递归图解了
4、二叉树的前序遍历
直达链接:二叉树的前序遍历
题目:
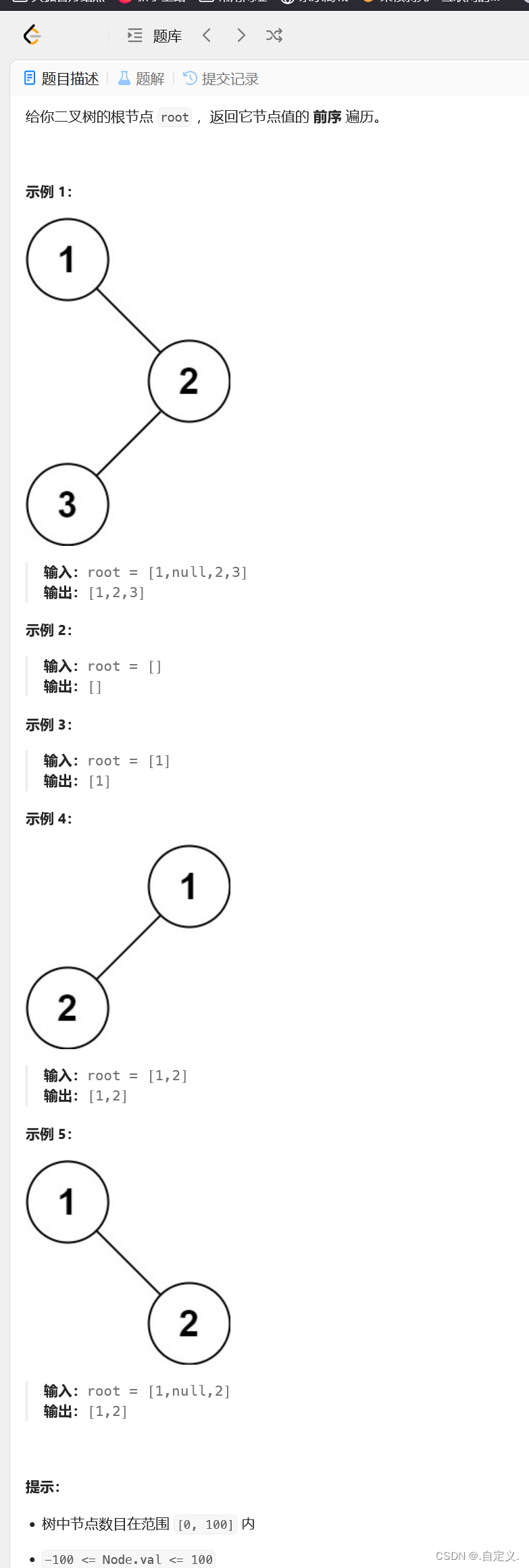 解题思路:
解题思路:
对于前序遍历在我之前的博客中已经讲到过,认真学习了的话对于前序遍历大家应该是小菜一点的
这题对第一次做的同学主要难的有两点:
1.对于解题框中preorderTraversal函数所传的实参int returnSize不知道什么意思
2.如何将前序遍历存入到一个数组中*
解题代码:
//计算树的节点
int Treesize(struct TreeNode* root)
{return root == NULL ?0 : Treesize(root->left)+Treesize(root->right)+1;
}void preorder(struct TreeNode* root,int*arr,int* i)
{if(root == NULL){return;}arr[(*i)++] = root->val;preorder(root->left,arr,i);preorder(root->right,arr,i);
}//return Size 返回数组的个数
int* preorderTraversal(struct TreeNode* root, int* returnSize) {(*returnSize) = Treesize(root);int* arr = (int*)malloc(sizeof(int)*(*returnSize));int i = 0;preorder(root,arr,&i);return arr;
}
代码讲解:
看了代码大家就会知道,returnSize其实是指所开辟数组空间数据的个数,这是力扣中写题的一贯格式,返回一个数组必须计算出其对应的空间大小。
对于如何将前序遍历存储到数组中我们看了代码我想大家就会明白,而这里需要注意的一点的访问数组的下标变量i使用的是地址,而不是数值,因为在调用函数前序遍历存储到数组中存储一个数据,下标i是需要加1往后进行移动的,而如果传数值进行下标的访问可能会出现在同一个下标位置多次存储的BUG,其原因就是形参只是实参的一份临时拷贝,而要想真正访问到实参所对应的数值就需要传指针进行解引用。
5、另一颗树的子树
直达链接:另一颗子树
题目:
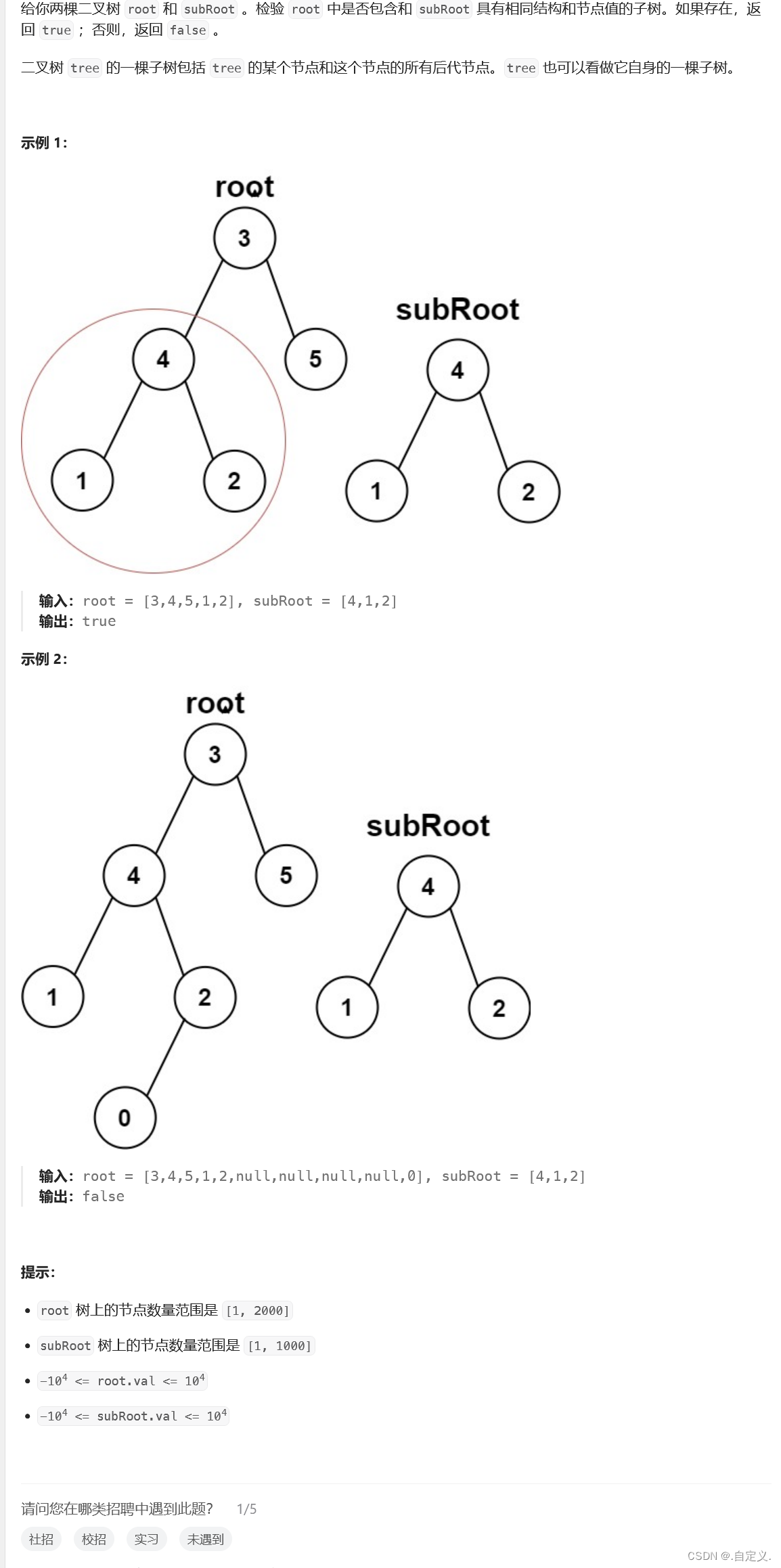 解题思路:
解题思路:
这题看似没有头绪,其实也不难
在判断是否含有子树时,我们可以直接调用之前写过的相等的树的题解(是不是恍然大悟😁)
那么我们需要判断的只有当root的节点值与subRoot的节点值相等时,直接进入判断当前子树与subRoot是否相等即可。
当然当递归到二叉树的叶子节点之后为空节点时说明root中不含有subRoot子树
解题代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//两个指针中有一个为空if(p == NULL && q == NULL){return true;}//其中有一个为空if(p == NULL || q == NULL){return false;}//两个指针都不为空if(p->val != q->val){return false;}return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(root == NULL){return false;}if(root->val == subRoot->val && isSameTree(root,subRoot)){return true;}return isSubtree(root->left,subRoot)|| isSubtree(root->right,subRoot);
}
我们以下面例子为大家进行递归图解:
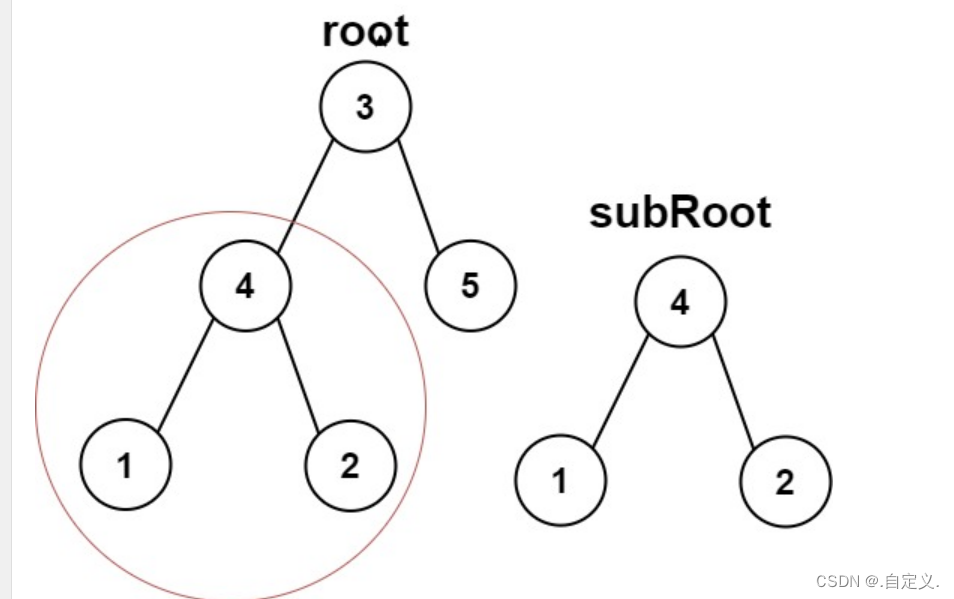
递归图解:
 注意最后判断对错用的||
注意最后判断对错用的||
大家可以跟着逻辑捋一遍逻辑(做完图才发现不能显示完整😭,上面递归图解逻辑是从中间开始的大家也可以自己手动绘个图)
完结撒❀
如果以上内容对你有帮助不妨点赞支持一下,以后还会分享更多编程知识,我们一起进步。
最后我想讲的是,据说点赞的都能找到漂亮女朋友❤

这篇关于数据结构刷题篇 之 【力扣二叉树基础OJ】详细讲解(含每道题链接及递归图解)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






