PTA Huffman Codes 思路分析及具体实现 v1.0

2024-03-29 14:38
文章标签 分析 实现 v1.0 思路 具体 pta huffman codes

本文主要是介绍PTA Huffman Codes 思路分析及具体实现 v1.0，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

PTA 7-9 Huffman Codes 思路分析及具体实现

  • 一、前导
    • 1. 写在前面
    • 2. 需要掌握的知识
    • 3. 题目信息
  • 二、解题思路分析
    • 1. 题意理解
    • 2. 思路分析（重点）
  • 三、具体实现
    • 1. 弯路和bug
    • 2. 代码框架（重点）
      • 2.1 采用的数据结构（重点）
      • 2.2 程序主体框架
      • 2.3 各分支函数（重点）
    • 3. 完整编码
  • 四、参考

一、前导

目前只做到了AC ( ╯□╰ )，代码质量惨不忍睹
21.10.13 ：对代码进行了优化

1. 写在前面

  1. 写博客的原因非常简单：好记性不如烂笔头。已经屡次被现实教育，虽然现在AC，如果下次再遇到，很可能重头开始
  2. 其次，对思路和走过的坑(遇到的bug)进行系统性梳理，有利于自己成长，AC并不是终点，而是另一个起点
  3. 和大家分享

2. 需要掌握的知识

  1. 这道题难度不小，如果对下面的知识点不熟悉，建议延后做
  2. Huffman树：具备最小WPL；满足前缀编码；没有节点为1的子树
  3. 前缀编码：任何一个字符的编码都不是其他字符编码的前缀
  4. 堆：这里的堆不是堆栈，而是一种特殊的数据结构，堆按照优先级排序，堆顶的元素是最小的(小顶堆)或最大的(大顶堆)，可以通过数组存储，通过完全二叉树表示。
  5. 编程能力：堆、树
  6. 其他：建堆和建Huffman树代码量都挺大，有很多大神在未建树的情况下也AC啦
    注意，本文介绍的是通过建Huffman树解决问题的方法，代码量还是蛮大的，如果说好处：那就是结合实际编码熟悉堆和哈夫曼树

3. 题目信息

题目来源：PTA / 拼题A
题目地址：https://pintia.cn/problem-sets/16/problems/671

二、解题思路分析

1. 题意理解

  1. 输入数据
//如下是输入数据
3  //需要编码的字符个数
a 1 b 1 c 2 //字符及其出现的频率
1 //提交编码的人数
a 00 //提交的编码
b 01 //提交的编码
c 1 //提交的编码
  1. 输出数据
    符合要求打印Yes，不符合输出No：print in each line either “Yes” if the student’s submission is correct, or “No” if not
  2. 题意
    对学生提交的编码进行判定，若wpl最小 且 编码正确(满足前缀编码的要求)，打印 Yes，否则打印 No

2. 思路分析（重点）

  1. 依据题意，围绕两点进行编码即可满足题目的判定要求：（1）提交的编码WPL(Weighted Path Length of Tree)是最小的（2）各字符编码满足前缀编码的要求。不需要考虑节点为1的判定条件。
    思考：如果一棵树wpl最小且满足前缀码要求，它有节点为1的子树吗？
    答：进行反证。
    假设存在子树为1的节点，该树的WPL最小 且 满足前缀编码的要求。首先，子树为1的节点不能存储数据，否则会破坏前缀编码要求。其次，数据一定存储在其下方的叶节点上，若拿掉子树为1的节点（确实可拿掉），WPL会减少 ，这个和 WPL最小矛盾。
    Alt
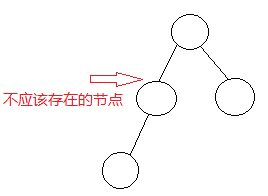
  2. 另外需要注意：Huffman树的WPL最小，但WPL最小的树不一定是Huffman树。只要WPL最小 且 满足前缀编码要求的学生答案都是正确的。
  3. 如何计算出最小WPL？如何确保编码满足前缀编码的需求？

三、具体实现

1. 弯路和bug

  1. 我一开始老想将元素(就是a 1 b 1 中的a,b )也通过结构体记录下来，最后发现完全没有必要，结构体中只存储频率即可。
    为什么不用记录元素？ WPL计算和前缀编码判定都是通过频率进行的，和元素没有任何关系。而且元素的顺序前后都是一致的。
  2. 我一开始思维始终局限在堆中的元素只能是int char 等单个元素，其实堆中的元素也可以是结构体，比如：树
  3. 注意别遗漏检查编码相同的异常情况，即 a b的编码结果都是 00
  4. 检查完一位学生后，需要恢复默认值

2. 代码框架（重点）

代码框架是我们容易忽视的内容，我们往往喜欢最快时间开始编码。其实就像盖房子，需要先画图纸然后再施工一样。程序也需要进行概要设计(框架)，再进行详细设计(Code)。需要先想好采用的数据结构 及 需要的函数

2.1 采用的数据结构（重点）

使用小顶堆的目的是为了创建Huffman树，每次从堆中取出两个频率最小的Huffman树，通过这两个Huffman树建一棵二叉树，然后将新建的树再插回小顶堆中。然后重复，上述操作需要执行N-1次(共N个元素)，最后形成一棵Huffman树

typedef struct TreeNode *HuffmanTree;
struct TreeNode
{int Weight;HuffmanTree Left,Right;
};//Huffman树的结构typedef struct HeapNode *MinHeap;
struct HeapNode  
{HuffmanTree *HTree;int Size;
};//堆结构，堆由一棵棵的Huffman树组成

2.2 程序主体框架

个人认为这个习惯很重要，先完成程序的大体框架并理清思路（详设）

               程序伪码描述
int main()
{	1.创建一个空的最小堆;2.接收录入的数据并创建一棵棵Huffman树，将这一棵棵树插入创建的最小堆中3.通过最小堆创建一棵Huffman树4.通过Huffman树得到wpl5.处理学生录入的数据：（1）计算其wpl，和得到的wpl比对 （2）判定是否满足前缀码要求6.打印判断结果return 0;
}

2.3 各分支函数（重点）

MinHeap CreatMinHeap(int n); //创建一个空堆
void InsertMinHeap(MinHeap H,HuffmanTree HTree ); //将元素插入到最小堆中
HuffmanTree DeleteMin(MinHeap H);
HuffmanTree Huffman(MinHeap H);
int WPL(HuffmanTree HTree,int depth); 
bool Judge(HuffmanTree HTree,bool value,bool end);
  1. CreatMinHeap() ：创建空堆。需要注意2点：（1）堆里存储的是一棵棵Huffman树，通过Weight进行排序；（2）设定好哨兵，也就是数组的0号
MinHeap CreatMinHeap(int n)
{MinHeap H;H=(MinHeap)malloc(sizeof(struct HeapNode));H->Size=0;H->HTree=(HuffmanTree*)malloc(sizeof(struct TreeNode)*(n+1)); //n棵Huffman树 + 1个哨兵 HuffmanTree tmp; //tmp是哨兵，其Weight是最小值tmp=(HuffmanTree)malloc(sizeof(struct TreeNode));tmp->Left=NULL;tmp->Right=NULL;tmp->Weight=-1;H->HTree[Guard]=tmp;return H;
}
  1. InsertMinHeap()：将一棵棵Huffman树插入到堆中，形成小顶堆。栗子：对于输入 a 1 b 1 c 2，可以把频率 1 1 2 看成三棵单节点的Huffman树
void InsertMinHeap(MinHeap H,HuffmanTree HTree)  
{int i = ++H->Size; for(; HTree->Weight < H->HTree[i/2]->Weight ; i=i/2 ){H->HTree[i]=H->HTree[i/2];  //堆中的元素是一棵棵的树，按频率进行排列。堆可以看作是一棵完全二叉树 }H->HTree[i]=HTree;return;
}
  1. DeleteMin()：目的是为了取出最小频率的子树，被Huffman()函数调用。Delete本身很简单，取出顶部的元素即可(数组序号是1)，编码难点是对剩余的元素进行调整，以便取出元素后剩余的元素仍然是小顶堆
HuffmanTree DeleteMin(MinHeap H)
{HuffmanTree HTree;HTree=H->HTree[Top]; H->HTree[Top]=H->HTree[H->Size--];int father,child; HuffmanTree tmp;father=Top; child=2*father; while(child <= H->Size)  //说明有儿子 {if( child+1 <= H->Size && H->HTree[child+1]->Weight < H->HTree[child]->Weight )child++;if(H->HTree[child]->Weight < H->HTree[father]->Weight){tmp=H->HTree[father];H->HTree[father]=H->HTree[child];H->HTree[child]=tmp;father=child;child=2*father;}elsebreak;	}return HTree;
}
  1. Huffman()：根据输入创建一棵Huffman树，为后续计算WPL打基础。创建Huffman树完全模拟Huffman树的建树过程，每次从集合中取出两棵频率最低的树，合并后放回原集合，然后重复N-1次(小顶堆共N个元素)
HuffmanTree Huffman(MinHeap H)
{int i; HuffmanTree T; int loop = H->Size;for(i=1; i<loop; i++) //bug:H->Size一直再变啊，需要固定住 {T=(HuffmanTree)malloc(sizeof(struct TreeNode)); T->Left=DeleteMin(H); T->Right=DeleteMin(H);T->Weight=T->Left->Weight + T->Right->Weight;InsertMinHeap(H,T); }T=DeleteMin(H);return T;
}
  1. WPL()：计算自己创建的Huffman树的wpl值，用于和学生提交的进行比对。通过递归实现比较容易
int WPL(HuffmanTree T,int depth)
{if(!T->Left && !T->Right)return (T->Weight*depth);else //由于是二叉树，一定有两个子树 {return (WPL(T->Left,depth+1) + WPL(T->Right,depth+1)); //depth++就是错的 why？ }	
}
  1. Judge(string a,string b)：判定学生的编码是否满足前缀编码（不存在二义性）
    21.10.13：编码不存在二义性，就是不能出现如下情况：001 0011 前者被后者包含 或 011 01 后者被前者包含
bool Judge(string a, string b)
{for (int i = 0; i < a.length() && i < b.length(); i++)if (a[i] != b[i])return true;return false;
}

以前的思路（不可取）：
思路是根据学生的录入创建Huffman树，然后在建树的过程中进行前缀码检查，模拟人工检查。我的Judge()实现的很不好，可以用惨不忍睹形容，这里就不列出了，后面我会找时间改进。
Judge函数的思路：模拟手动检查，如果遇到0，新建一棵左子树 或 向左子树下移一格 ； 如果遇到1，新建一棵右子树 或 向右子树下移一格。特殊的，编码的最后一位：判定其下方是否有左右子树 ；若有，左右子树 Weight值为 1 时 违反前缀码 。注意别遗漏检查编码相同的情况，即 a b的编码结果都是 00

3. 完整编码

21.10.13的AC代码：靠之前的自己续命 + 帮助以前的自己，这道题是一场苦战

#include <iostream>
using namespace std;typedef struct TreeNode* HuffmanTree;
typedef struct Heap *MinHeap; //将MinHeap切换为*MinHeap，使用指针更灵活，将其作为参数传入，效果类似实参：可以真正改变（这个理解不严谨）struct Heap
{HuffmanTree *HTree; //存放哈夫曼树的数组int Size;//不统计哨兵
};struct TreeNode
{	//A 1 B 1 C 1 D 3 E 3 F 6 G 6int Freq;//为什么不记录A B C 只记录频率1 1 1? 因为根据哈夫曼树的特点，待计算WPL的结点都位于叶结点（知道出现频率就可以了）HuffmanTree Left;HuffmanTree Right;
};MinHeap CreateEmptyHeap(int N);
void InsertHeap(MinHeap MHeap, HuffmanTree HTree);HuffmanTree DeleteHeap(MinHeap MHeap); //从小顶堆中取出最小的Huffman树
HuffmanTree ConstructHuffman(MinHeap MHeap); //依次取出两个Huffman树，合并后插入原堆中，重复，直到Size=1;int CalcWPL(HuffmanTree Tree,int Height);
bool Judge(string a, string b);int main()
{int N;  cin >> N;MinHeap MHeap = CreateEmptyHeap(N);int* a = new int[N]; //存储所有元素出现的频率 计算WPL会用上char Symbol; int Freq;for (int i = 0; i < N; i++)//A 1 B 1 C 1 D 3 E 3 F 6 G 6{cin >> Symbol >> Freq;a[i] = Freq;HuffmanTree HTree;HTree = new struct TreeNode;HTree->Freq = Freq;HTree->Left = HTree->Right = NULL;InsertHeap(MHeap, HTree); //二叉树构建的最小堆 完毕}HuffmanTree Reference;Reference = ConstructHuffman(MHeap);int RefWPL = CalcWPL(Reference, 0);int Student; cin >> Student;string Code; string* b = new string[N];//数组b用于记录编码for (int i = 0; i < Student; i++){int StuWPL = 0;for (int i = 0; i < N; i++){cin >> Symbol >> Code;b[i] = Code;StuWPL += Code.length() * a[i];}bool Flag = true;if (RefWPL == StuWPL)//WPL一致的情况下 判定是否存在二义性{for (int i = 0; i < N && Flag; i++)for (int j = i + 1; j < N && Flag; j++)Flag = Judge(b[i], b[j]);			if (Flag)cout << "Yes" << endl;elsecout << "No" << endl;}elsecout << "No" << endl;}return 0;
}bool Judge(string a, string b)
{for (int i = 0; i < a.length() && i < b.length(); i++)if (a[i] != b[i])return true;return false;
}int CalcWPL(HuffmanTree Tree, int Height)
{if (!Tree->Left && !Tree->Right) //叶结点就是待计算的结点return Tree->Freq * Height;elsereturn CalcWPL(Tree->Left, Height + 1) + CalcWPL(Tree->Right, Height + 1);
}HuffmanTree DeleteHeap(MinHeap MHeap)
{HuffmanTree Tree = MHeap->HTree[1];//取出最小的Huffman树的index=1 , 0 is Guard//将剩余的元素再次调整为最小堆MHeap->HTree[1] = MHeap->HTree[MHeap->Size--];int Parent = 1, Child = Parent * 2;while (Child <= MHeap->Size){if ((Child + 1 <= MHeap->Size) && (MHeap->HTree[Child + 1]->Freq < MHeap->HTree[Child]->Freq))Child++;HuffmanTree Tmp;if (MHeap->HTree[Child]->Freq < MHeap->HTree[Parent]->Freq){Tmp = MHeap->HTree[Parent];MHeap->HTree[Parent] = MHeap->HTree[Child];MHeap->HTree[Child] = Tmp;Parent = Child;Child = Parent * 2;}elsebreak;}return Tree;
}HuffmanTree ConstructHuffman(MinHeap MHeap)
{int Loop = MHeap->Size - 1;HuffmanTree Tree01, Tree02,Tree;for (int i = 0; i < Loop; i++){Tree01 = DeleteHeap(MHeap);Tree02 = DeleteHeap(MHeap);Tree = new struct TreeNode;Tree->Freq = Tree01->Freq + Tree02->Freq;Tree->Left = Tree01; Tree->Right = Tree02;InsertHeap(MHeap, Tree);}return DeleteHeap(MHeap);
}void InsertHeap(MinHeap MHeap, HuffmanTree HTree)
{	int i = ++MHeap->Size; //在堆中可能的插入位置while (HTree->Freq < MHeap->HTree[i/2]->Freq) //调整为小顶堆{MHeap->HTree[i] = MHeap->HTree[i/2];i /= 2;}MHeap->HTree[i] = HTree;return ;
}MinHeap CreateEmptyHeap(int N)
{MinHeap MHeap; MHeap = new struct Heap;MHeap->Size = 0;MHeap->HTree = new HuffmanTree[N + 1]; //0是哨兵 + N个元素HuffmanTree Guard = new struct TreeNode;//哨兵Guard->Freq = -1;Guard->Left = Guard->Right = NULL;MHeap->HTree[MHeap->Size] = Guard; //哨兵不算正式元素，因此 MHeap->HTree[MHeap->Size++] = Guard 是错误的;return MHeap;
}
/*
0.数据结构：（1）通过结构体存储堆、堆由一棵棵哈夫曼树构成（2）根据Huffman树的特点，待统计WPL的结点都处于叶结点
1.构建Huffman树：（1）最小堆（由一颗颗树构成）（2）每次取出两个最小的树->处理后放回最小堆->再取出两个最小的...直到全部取出（3）取出意味着堆删除元素，插入意味堆新增元素
2.构建完毕，统计WPL
3.判定：（1）最小编码长度应该相同 （2）编码不存在二义性,即不能出现如下情况：001 0011 前者被后者包含 或 011 01 后者被前者包含
*/

之前的AC代码

#include <cstring>
#include <queue>
#include <cstdlib>
#include <iostream>
using namespace std;#define Top 1
#define Guard 0    //7   A 1 B 1 C 1 D 3 E 3 F 6 G 6
#define Max 100typedef char ElementType;   //不记录元素，只记录频率试试typedef struct TreeNode *HuffmanTree;
struct TreeNode
{int Weight;HuffmanTree Left,Right;
};typedef struct HeapNode *MinHeap;
struct HeapNode  
{HuffmanTree *HTree;int Size;
};HuffmanTree DeleteMin(MinHeap H);void InsertMinHeap(MinHeap H,HuffmanTree HTree );
MinHeap CreatMinHeap(int n);
HuffmanTree Huffman(MinHeap H);
void PrintTree(HuffmanTree T);
void PrintHeap(MinHeap H);
int WPL(HuffmanTree HTree,int depth); 
bool Judge(HuffmanTree HTree,bool value,bool end);int main()
{	int n;cin>>n;MinHeap H;H=CreatMinHeap(n);ElementType data;int freq;HuffmanTree HTree;   int a[n]; for(int i=0;i<n;i++){cin>>data>>freq;a[i]=freq;HTree=(HuffmanTree)malloc(sizeof(struct TreeNode));HTree->Weight= freq; HTree->Left=NULL; HTree->Right=NULL; //每棵树都是单节点 InsertMinHeap(H,HTree);}HTree=Huffman(H); int wpl;wpl=WPL(HTree,0);HuffmanTree  Judge_Tree , Judge_Tree_bak;Judge_Tree=(HuffmanTree)malloc(sizeof(struct TreeNode));Judge_Tree->Weight=0;Judge_Tree->Left=NULL;Judge_Tree->Right=NULL;Judge_Tree_bak=Judge_Tree;int m; // m represent student's numbercin>>m;char code[Max]; bool flag=1; int current_wpl=0; int tmp; bool end=0;for(int i=0;i<m;i++){for(int j=0;j<n;j++){cin>>data>>code; //A 00000current_wpl=current_wpl+a[j]*strlen(code);if(flag==false) continue;for(int k=0;k<strlen(code);k++) //根据编码进行建树 {tmp=code[k]-'0';if(k== (strlen(code)-1) ) end=1;flag=Judge(Judge_Tree,tmp,end);if(tmp==0) {//cout<<"go left subtree "<<endl;Judge_Tree=Judge_Tree->Left;}else {//cout<<"go right subtree "<<endl;Judge_Tree=Judge_Tree->Right;}} //loop endJudge_Tree=Judge_Tree_bak;end=0;}Judge_Tree->Left=NULL; Judge_Tree->Right=NULL;//cout<<"current_wpl:"<<current_wpl<<endl;if(current_wpl!=wpl) flag=0;if(flag==1) cout<<"Yes"<<endl;else cout<<"No"<<endl;	flag=1;current_wpl=0; //fix bug, add this code.}//}return 0;
}bool Judge(HuffmanTree HTree,bool value,bool end)
{//bool flag==1;if(value==0 && !HTree->Left && end!=1)  //{//cout<<"value==0 && !HTree->Left && end!=1"<<endl;HuffmanTree T;T=(HuffmanTree)malloc(sizeof(struct TreeNode));T->Weight=0;T->Left=NULL;T->Right=NULL; //bug  no defalut valueHTree->Left=T;//HTree=HTree->Left;return true;}if(value==0 && !HTree->Left && end==1){//cout<<"value==0 && !HTree->Left && end==1"<<endl;HuffmanTree T;T=(HuffmanTree)malloc(sizeof(struct TreeNode));T->Weight=1;T->Left=NULL;T->Right=NULL;HTree->Left=T;//HTree=HTree->Left;	return true;	}if(value==0 && HTree->Left && end!=1){//cout<<"value==0 && HTree->Left && end!=1"<<endl;//HTree=HTree->Left;return true;}if(value==0 && HTree->Left && end==1){//cout<<"value==0 && HTree->Left && end==1 "<<endl;HuffmanTree bak;HTree=HTree->Left;if(HTree->Weight==1) return false;else HTree->Weight=1;bak=HTree;while(HTree->Left){if(HTree->Left->Weight==1){//cout<<"got it!!!"<<endl;return false;}HTree=HTree->Left;}HTree=bak;while(HTree->Right){if(HTree->Right->Weight==1){//cout<<"got it!!!"<<endl;return false;}HTree=HTree->Right;}//HTree=bak;return true;}// -------------------sepereate-------------------------------if(value==1 && !HTree->Right && end!=1)  //{//cout<<"value==1 && !HTree->Right && end!=1"<<endl;HuffmanTree T;T=(HuffmanTree)malloc(sizeof(struct TreeNode));T->Weight=0;T->Left=NULL;T->Right=NULL;HTree->Right=T;//HTree=HTree->Right;return true;}if(value==1 && !HTree->Right && end==1){//cout<<"value==1 && !HTree->Right && end==1"<<endl;HuffmanTree T;T=(HuffmanTree)malloc(sizeof(struct TreeNode));T->Weight=1;T->Left=NULL;T->Right=NULL;HTree->Right=T;//HTree=HTree->Right;return true;}if(value==1 && HTree->Right && end!=1){//HTree=HTree->Right;//cout<<"value==1 && HTree->Right && end!=1"<<endl;return true;}if(value==1 && HTree->Right && end==1){//cout<<"Here is value==1 && HTree->Right && end==1" <<endl;HuffmanTree bak;HTree=HTree->Right;if(HTree->Weight==1) return false;else HTree->Weight=1;bak=HTree;while(HTree->Right){if(HTree->Right->Weight==1){//cout<<"got it!!!"<<endl;return false;}HTree=HTree->Right;}HTree=bak;while(HTree->Left){if(HTree->Left->Weight==1){//cout<<"got it!!!"<<endl;return false;}HTree=HTree->Left;}//HTree=bak;return true;}//return true; 
}int WPL(HuffmanTree T,int depth)
{//int wpl;if(!T->Left && !T->Right)return (T->Weight*depth);else //由于是二叉树，一定有两个子树 {return (WPL(T->Left,depth+1) + WPL(T->Right,depth+1)); //depth++就是错的 why？ }//return wpl;}void PrintHeap(MinHeap H)
{for(int i=1;i<=H->Size;i++)cout<<H->HTree[i]->Weight<<endl;
} void PrintTree(HuffmanTree T)
{HuffmanTree HTree,x;HTree=T;queue<HuffmanTree> q; q.push(HTree);while(!q.empty()){x=q.front();cout<<x->Weight<<' ';q.pop();//q.push(T->Left->Weight);   //没有子树如何处理  如何自动打印 //q.push(T->Right->Weight);if(x->Left) {q.push(x->Left);}if(x->Right){q.push(x->Right);}//T=T->Left}return;
}HuffmanTree DeleteMin(MinHeap H)
{//cout<<"Here is Del Fun."<<endl;HuffmanTree HTree;HTree=H->HTree[Top]; H->HTree[Top]=H->HTree[H->Size--];int father,child; HuffmanTree tmp;father=Top; child=2*father; while(child <= H->Size)  //说明有儿子 {if( child+1 <= H->Size && H->HTree[child+1]->Weight < H->HTree[child]->Weight )child++;if(H->HTree[child]->Weight < H->HTree[father]->Weight){tmp=H->HTree[father];H->HTree[father]=H->HTree[child];H->HTree[child]=tmp;father=child;child=2*father;}elsebreak;	}//H->Frequent[H->Size--];return HTree;
}HuffmanTree Huffman(MinHeap H)
{int i; HuffmanTree T; int loop = H->Size;for(i=1; i<loop; i++) //bug:H->Size一直再变啊，需要固定住 {T=(HuffmanTree)malloc(sizeof(struct TreeNode)); T->Left=DeleteMin(H); //bug? //PrintTree(T->Left);T->Right=DeleteMin(H);//PrintTree(T->Right);T->Weight=T->Left->Weight + T->Right->Weight;InsertMinHeap(H,T);  //bug?}T=DeleteMin(H);//cout<<"Print the Final T..."<<endl;//PrintTree(T);return T;
}
void InsertMinHeap(MinHeap H,HuffmanTree HTree)  //Insert(H,T); //Insert???
{int i = ++H->Size; for(; HTree->Weight < H->HTree[i/2]->Weight ; i=i/2 ){H->HTree[i]=H->HTree[i/2];  //堆中的元素是一棵棵的树，按频率进行排列。堆 完全二叉树 }H->HTree[i]=HTree;return;
}MinHeap CreatMinHeap(int n)
{//cout<<"Here is Create Func."<<endl;MinHeap H;H=(MinHeap)malloc(sizeof(struct HeapNode));H->Size=0;H->HTree=(HuffmanTree*)malloc(sizeof(struct TreeNode)*(n+1)); //通过指针表示数组 HuffmanTree tmp;tmp=(HuffmanTree)malloc(sizeof(struct TreeNode));tmp->Left=NULL;tmp->Right=NULL;tmp->Weight=-1;H->HTree[Guard]=tmp;return H;
}

四、参考

  1. 浙大 陈越、何钦铭老师主讲的数据结构: http://www.icourse163.org/learn/ZJU-93001?tid=1459700443#/learn/content?type=detail&id=1235254062.

这篇关于PTA Huffman Codes 思路分析及具体实现 v1.0的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/858854。

相关文章

使用Python实现IP地址和端口状态检测与监控

使用Python实现IP地址和端口状态检测与监控

《使用Python实现IP地址和端口状态检测与监控》在网络运维和服务器管理中,IP地址和端口的可用性监控是保障业务连续性的基础需求,本文将带你用Python从零打造一个高可用IP监控系统,感兴趣的小伙... 目录概述：为什么需要IP监控系统使用步骤说明1. 环境准备2. 系统部署3. 核心功能配置系统效果展
阅读更多...
Python实现微信自动锁定工具

Python实现微信自动锁定工具

《Python实现微信自动锁定工具》在数字化办公时代,微信已成为职场沟通的重要工具,但临时离开时忘记锁屏可能导致敏感信息泄露,下面我们就来看看如何使用Python打造一个微信自动锁定工具吧... 目录引言：当微信隐私遇到自动化守护效果展示核心功能全景图技术亮点深度解析1. 无操作检测引擎2. 微信路径智能获
阅读更多...
Python中pywin32 常用窗口操作的实现

Python中pywin32 常用窗口操作的实现

《Python中pywin32常用窗口操作的实现》本文主要介绍了Python中pywin32常用窗口操作的实现,pywin32主要的作用是供Python开发者快速调用WindowsAPI的一个... 目录获取窗口句柄获取最前端窗口句柄获取指定坐标处的窗口根据窗口的完整标题匹配获取句柄根据窗口的类别匹配获取句
阅读更多...
在 Spring Boot 中实现异常处理最佳实践

在 Spring Boot 中实现异常处理最佳实践

《在SpringBoot中实现异常处理最佳实践》本文介绍如何在SpringBoot中实现异常处理,涵盖核心概念、实现方法、与先前查询的集成、性能分析、常见问题和最佳实践,感兴趣的朋友一起看看吧... 目录一、Spring Boot 异常处理的背景与核心概念1.1 为什么需要异常处理？1.2 Spring B
阅读更多...
Python中的Walrus运算符分析示例详解

Python中的Walrus运算符分析示例详解

《Python中的Walrus运算符分析示例详解》Python中的Walrus运算符（:=）是Python3.8引入的一个新特性,允许在表达式中同时赋值和返回值,它的核心作用是减少重复计算,提升代码简... 目录1. 在循环中避免重复计算2. 在条件判断中同时赋值变量3. 在列表推导式或字典推导式中简化逻辑
阅读更多...
Python位移操作和位运算的实现示例

Python位移操作和位运算的实现示例

《Python位移操作和位运算的实现示例》本文主要介绍了Python位移操作和位运算的实现示例,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一... 目录1. 位移操作1.1 左移操作 (<<)1.2 右移操作 (>>)注意事项：2. 位运算2.1
阅读更多...
如何在 Spring Boot 中实现 FreeMarker 模板

如何在 Spring Boot 中实现 FreeMarker 模板

《如何在SpringBoot中实现FreeMarker模板》FreeMarker是一种功能强大、轻量级的模板引擎,用于在Java应用中生成动态文本输出（如HTML、XML、邮件内容等）,本文... 目录什么是 FreeMarker 模板？在 Spring Boot 中实现 FreeMarker 模板1. 环
阅读更多...
Qt实现网络数据解析的方法总结

Qt实现网络数据解析的方法总结

《Qt实现网络数据解析的方法总结》在Qt中解析网络数据通常涉及接收原始字节流,并将其转换为有意义的应用层数据,这篇文章为大家介绍了详细步骤和示例,感兴趣的小伙伴可以了解下... 目录1. 网络数据接收2. 缓冲区管理（处理粘包/拆包）3. 常见数据格式解析3.1 jsON解析3.2 XML解析3.3 自定义
阅读更多...
SpringMVC 通过ajax 前后端数据交互的实现方法

SpringMVC 通过ajax 前后端数据交互的实现方法

《SpringMVC通过ajax前后端数据交互的实现方法》：本文主要介绍SpringMVC通过ajax前后端数据交互的实现方法,本文给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价... 在前端的开发过程中，经常在html页面通过AJAX进行前后端数据的交互，SpringMVC的controll
阅读更多...
Spring Security自定义身份认证的实现方法

Spring Security自定义身份认证的实现方法

《SpringSecurity自定义身份认证的实现方法》：本文主要介绍SpringSecurity自定义身份认证的实现方法,下面对SpringSecurity的这三种自定义身份认证进行详细讲解,... 目录1.内存身份认证（1）创建配置类（2）验证内存身份认证2.JDBC身份认证（1）数据准备 （2）配置依
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2