本文主要是介绍hdu 1116 Play on Words(并查集+欧拉回路|| 欧拉路径),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目:http://acm.hust.edu.cn/vjudge/problem/viewProblem.action?id=18117
Description
Some of the secret doors contain a very interesting word puzzle. The team of archaeologists has to solve it to open that doors. Because there is no other way to open the doors, the puzzle is very important for us.
There is a large number of magnetic plates on every door. Every plate has one word written on it. The plates must be arranged into a sequence in such a way that every word begins with the same letter as the previous word ends. For example, the word ``acm'' can be followed by the word ``motorola''. Your task is to write a computer program that will read the list of words and determine whether it is possible to arrange all of the plates in a sequence (according to the given rule) and consequently to open the door.
There is a large number of magnetic plates on every door. Every plate has one word written on it. The plates must be arranged into a sequence in such a way that every word begins with the same letter as the previous word ends. For example, the word ``acm'' can be followed by the word ``motorola''. Your task is to write a computer program that will read the list of words and determine whether it is possible to arrange all of the plates in a sequence (according to the given rule) and consequently to open the door.
Input
The input consists of T test cases. The number of them (T) is given on the first line of the input file. Each test case begins with a line containing a single integer number Nthat indicates the number of plates (1 <= N <= 100000). Then exactly Nlines follow, each containing a single word. Each word contains at least two and at most 1000 lowercase characters, that means only letters 'a' through 'z' will appear in the word. The same word may appear several times in the list.
Output
Your program has to determine whether it is possible to arrange all the plates in a sequence such that the first letter of each word is equal to the last letter of the previous word. All the plates from the list must be used, each exactly once. The words mentioned several times must be used that number of times.
If there exists such an ordering of plates, your program should print the sentence "Ordering is possible.". Otherwise, output the sentence "The door cannot be opened.".
If there exists such an ordering of plates, your program should print the sentence "Ordering is possible.". Otherwise, output the sentence "The door cannot be opened.".
Sample Input
3 2 acm ibm 3 acm malform mouse 2 ok ok
Sample Output
The door cannot be opened. Ordering is possible. The door cannot be opened.
通过图(无向图或有向图)中所有边且每边仅通过一次通路称为欧拉通路,相应的回路称为欧拉回路。具有欧拉回路的图称为欧拉图(Euler Graph),具有欧拉通路而无欧拉回路的图称为半欧拉图。
相关定理:
1.无向连通图G是欧拉图,当且仅当G不含奇数度结点(G的所有结点度数为偶数);
2.无向连通图G含有欧拉通路,当且仅当G有零个或两个奇数度的结点;
3.有向连通图D是欧拉图,当且仅当该图为连通图且D中每个结点的入度=出度
4.有向连通图D含有欧拉通路,当且仅当该图为连通图且D中除两个结点外,其余每个结点的入度=出度,且此两点满足deg-(u)-deg+(v)=±1。(起始点s的入度=出度-1,结束点t的出度=入度-1 或两个点的入度=出度)
再说明一下连通的相关概念:强连通图(Strongly Connected Graph)是指一个有向图(Directed Graph)中任意两点v1、v2间存在v1到v2的路径(path)及v2到v1的路径的图。弱连通图:如果不考虑有向图中边的方向所得到的无向图是连通图,则有向图称为弱连通图可以从某一顶点起遍历到子图中所有的顶点,但并非从其他顶点也能做到的极大有向子图。比如:
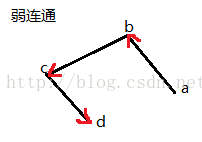
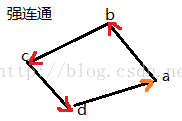
有关欧拉图的例子:
1.哥尼斯堡七桥问题:18世纪哥尼斯堡(后来的加里宁格勒)位于立陶宛的普雷格尔上有7座桥,将河中的两个岛和河岸连结,如图1所示。城中的居民经常沿河过桥散步,于是提出了一个问题:能否一次走遍7座桥,而每座桥只许通过一次,最后仍回到起始地点。这就是七桥问题,一个著名的图论问题。

明显,四个点全是奇点(度是奇数),所以不可能完成任务。
欧拉回路的例子:
2.一个邮递员投递信件要走的街道如下左图所示,图中的数字表示各条街道的千米数,他从邮局出发,要走遍各街道,最后回到邮局。怎样走才能使所走的行程最短?全程多少千米?
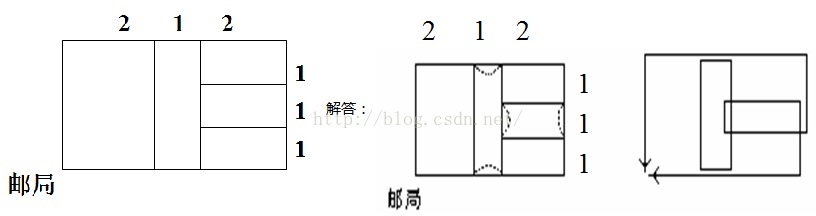
通过加上4条边把8个奇点全部消除就能形成一个欧拉回路,全程34千米(走法不唯一)。
欧拉路径:
3.每个小正方形的边长都是100米。小明沿线段从A点到B点,不许走重复路,他最多能走多少米?
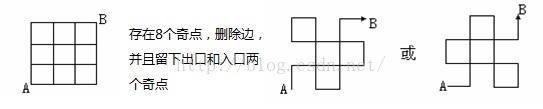
去掉6条线段,走1800米。
好的,应该明白欧拉路径和欧拉回路的意思了。
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int in[30],out[30],f[30],vis[30];
int find(int x){if(x==f[x]) return x;f[x]=find(f[x]);return f[x];
}
void init(){memset(in,0,sizeof(in));memset(out,0,sizeof(out));memset(vis,0,sizeof(vis));for(int i=0;i<30;i++)f[i]=i;
}
char str[1005];
int main()
{//freopen("cin.txt","r",stdin);int t,n;cin>>t;while(t--){init();scanf("%d",&n);while(n--){scanf("%s",str);int q1=str[0]-'a',q2=str[strlen(str)-1]-'a';out[q1]++;in[q2]++;vis[q1]=vis[q2]=1;f[q1]=f[q2]=find(q1);}int judge=0;for(int i=0;i<26;i++){if(vis[i]&&f[i]==i){ judge++; } // f[i]!=f[0] is wrong}if(judge>1){printf("The door cannot be opened.\n");continue;}int head=0,tail=0,other=0;for(int i=0;i<26;i++){if(vis[i]&&out[i]!=in[i]){if(out[i]+1==in[i]) tail++;else if(in[i]+1==out[i]) head++;else other++;}}if(other>0){printf("The door cannot be opened.\n");continue;}if((head==0&&tail==0) || (head==1&&tail==1)) {printf("Ordering is possible.\n");continue;}printf("The door cannot be opened.\n");}return 0;
}当head==0&&tail==0时形成欧拉回路,当head==1&&tail==1时形成欧拉路径。
其实,并查集相连的不是单词,而是单个单词的首字符和尾字符,同一个字符有进(in)必有出(out)。
这篇关于hdu 1116 Play on Words(并查集+欧拉回路|| 欧拉路径)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




