利用北斗BDS广播星历，进行卫星位置计算

2024-03-25 11:30
文章标签 进行 广播 计算 位置 卫星 北斗 bds 星历

本文主要是介绍利用北斗BDS广播星历，进行卫星位置计算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

一、北斗星历数据获取

1.1 计算卫星位置需要用到的星历数据：

1.2 计算卫星位置需要用到的常数

二、toc时刻计算

三、根据卫星发射时刻Tsv，计算卫星轨道参数

3.1 修正Tsv的卫星钟偏

3.2 计算规划时间

3.3 计算平近点角

3.4 迭代求解偏近点角

3.5 求解真近点角和升交点角距

3.6 轨道参数计算，并考虑摄动改正项

四、计算Tsv时刻的卫星位置

4.1 MEO/IGSO卫星位置计算

4.2 GEO卫星位置计算

五、计算Tsv时刻的卫星速度

六、计算卫星钟偏

七、MATLAB代码&运行示例

一、北斗星历数据获取

北斗广播星历获取途径：RINEX格式文件、导航电文解码。

下面以RINEX格式文件为例：

这里给出的北斗卫星分别是：C05  GEO卫星、C16  MEO/IGSO卫星。这是两种不同轨道的北斗卫星：GEO地球静止轨道卫星、MEO中圆地球轨道卫星、IGSO倾斜地球同步轨道卫星。其GEO卫星位置的计算方法与MEO/IGSO卫星不同，下面过程注意区分。

     3.05           N: GNSS NAV DATA    C: BDS              RINEX VERSION / TYPE
BNC 2.13.0          BKG Frankfurt       20231102 101016 UTC PGM / RUN BY / DATE
Concatenated RINEX files (8)                                COMMENTEND OF HEADER
C05 23 11 02 08 00 00.0 1.385881332680e-04-6.030731469760e-11 0.000000000000e+001.000000000000e+00-2.278125000000e+02-5.663093033410e-09-6.708219322780e-01-7.327646017070e-06 7.320673903450e-04-1.202011480930e-05 6.493444162370e+033.744000000000e+05-5.634501576420e-08-6.255581541050e-01 3.259629011150e-089.409420036110e-02 3.626718750000e+02-1.792511645600e+00 6.869929017260e-092.378670509750e-10                    9.300000000000e+02                   2.000000000000e+00 0.000000000000e+00 2.999999970670e-10-9.100000000000e-093.779100000000e+05 0.000000000000e+00                                      
C16 23 11 02 08 00 00.0-1.551879104230e-04-1.854782993860e-11 0.000000000000e+001.000000000000e+00-3.535937500000e+01 1.561493613910e-09-2.192800555490e+00-1.096632331610e-06 6.275521009230e-03 8.363742381330e-06 6.493531814580e+033.744000000000e+05-2.700835466380e-08 2.343958791130e+00 5.215406417850e-089.618269834520e-01-8.421875000000e+00-2.286522345190e+00-1.925437345050e-09-7.286017777600e-11                    9.300000000000e+02                   2.000000000000e+00 0.000000000000e+00-2.499999984810e-09 4.800000000000e-093.744000000000e+05 0.000000000000e+00

1.1 计算卫星位置需要用到的星历数据：

1、星历参考时刻 toc：第一行第一个数据   23 11 02 08 00 00.0

2、卫星钟差 af0：第一行第二个数据   1.385881332680e-04

3、卫星钟偏 af1：第一行第三个数据   -6.030731469760e-11

4、卫星钟偏移 af2：第一行第四个数据   0.000000000000e+00

5、轨道半径改正项 Crs：第二行第二个数据   -2.278125000000e+02

6、角速度改正项 deltan：第二行第三个数据   -5.663093033410e-09

7、平近点角 M0：第二行第四个数据   -6.708219322780e-01

8、升交点角距改正 Cuc：第三行第一个数据   -7.327646017070e-06

9、偏心率 e：第三行第二个数据   7.320673903450e-04

10、升交点角距改正 Cus：第三行第三个数据   -1.202011480930e-05

11、轨道长半轴 sqrtA：第三行第四个数据   6.493444162370e+03

12、周内秒 toe：第四行第一个数据   3.744000000000e+05

13、轨道倾角改正项 Cic：第四行第二个数据   -5.634501576420e-08

14、升交点赤经 omega0：第四行第三个数据   -6.255581541050e-01

15、轨道倾角改正项 Cis：第四行第四个数据   3.259629011150e-08

16、轨道倾角 i0：第五行第一个数据   9.409420036110e-02

17、轨道半径改正项 Crc：第五行第二个数据   3.626718750000e+02

18、近地点角距 omega：第五行第三个数据   -1.792511645600e+00

19、赤经变化 omegaDot：第五行第四个数据   6.869929017260e-09

20、轨道倾角变率 IDOT：第六行第一个数据   2.378670509750e-10

21、卫星设备时延 TGD1：第七行第三个数据   2.999999970670e-10

1.2 计算卫星位置需要用到的常数

1、圆周率 pi：3.1415926535898

2、地球自转角速度 radv：7.2921151467e-5

3、地球标准引力常数 GM：3.986005e14

4、地球引力常数 F：-4.442807633e-10

二、toc时刻计算

从RINEX文件中获取到的toc时刻是年月日时分秒的形式，toc时刻要将其化成周内秒的形式。比如：23 11 02 08 00 00.0代表的是2023年11月2日即周四的 8:00，其周内秒 toc = 4*24*3600+8*3600，toc = 374400s。我们发现 toc = toe，toc时刻与toe时刻是同步的。

三、根据卫星发射时刻Tsv，计算卫星轨道参数

3.1 修正Tsv的卫星钟偏

卫星的真实发射时刻Tsv由初始Tsv修正卫星钟偏和卫星设备时延后得到，并且这里的Tsv也是周内秒的形式：

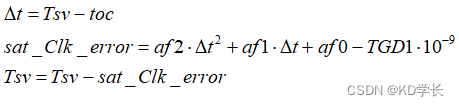
其中sat_Clk_error表示卫星钟偏。

3.2 计算规划时间

星历中的toe时刻，表示星历中的所有卫星数据是toe时刻瞬间的。发射时间Tsv的卫星数据，需要通过 Tsv-toe 的差值进行计算，这个差就叫规划时间tk。

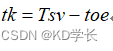
3.3 计算平近点角

轨道长半轴：

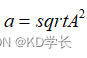
平均角速度：

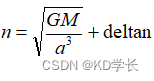
平近点角：

3.4 迭代求解偏近点角

偏近点角的计算公式：

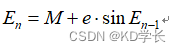
为了偏近点角的准确性，采用迭代的过程求解。

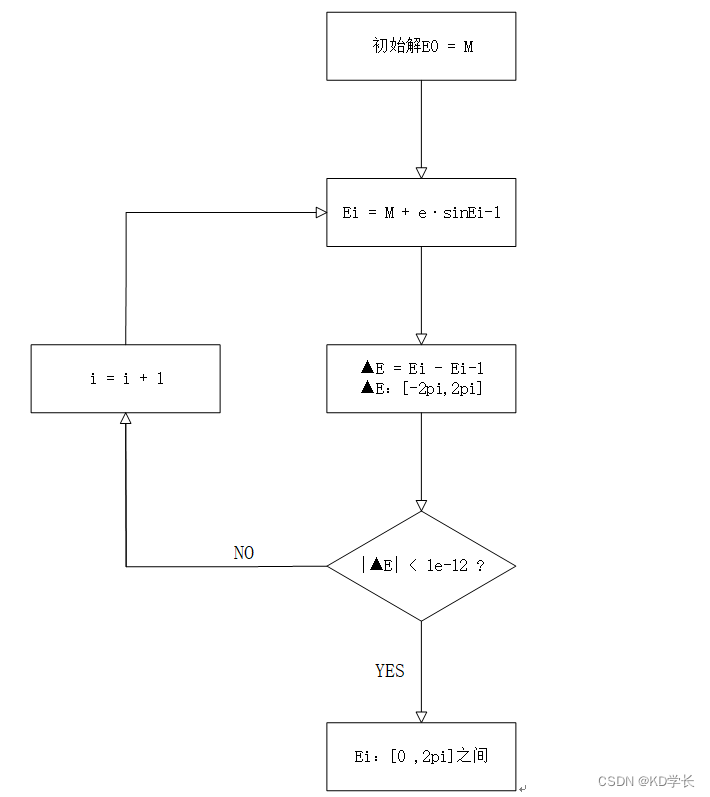
3.5 求解真近点角和升交点角距

真近点角：

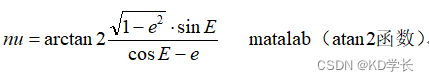
升交点角距：

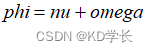
3.6 轨道参数计算，并考虑摄动改正项

升交点角距改正项：

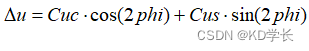
轨道半径改正项：

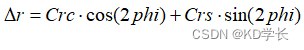
轨道倾角改正项：

升交点角距：

轨道半径：

轨道倾角：

升交点赤经：

如果是GEO卫星升交点赤经计算公式如下：

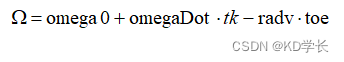
如果是MEO/IGSO卫星升交点赤经计算公式如下：

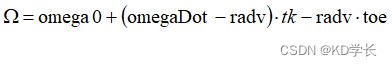
四、计算Tsv时刻的卫星位置

根据上面的计算，已经得到了Tsv时刻的卫星轨道参数：升交点角距、轨道半径、轨道倾角、升交点赤经。

4.1 MEO/IGSO卫星位置计算

MEO/IGSO卫星位置的ECEF坐标，可由下面公式计算得到：

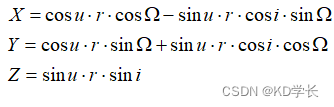
4.2 GEO卫星位置计算

GEO卫星位置的ECEF坐标，可由下面公式计算得到：

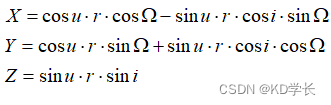
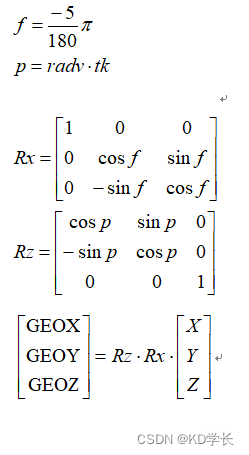
五、计算Tsv时刻的卫星速度

根据上面的计算，已经得到了Tsv时刻的卫星轨道速度参数：平均角速度 n、偏近点角 E、偏心率 e、升交点角距 phi 等。

卫星 (X,Y,Z) 三个方向上的速度，可根据下面公式得到：

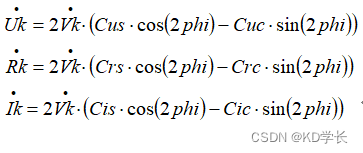
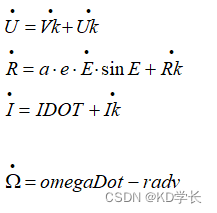
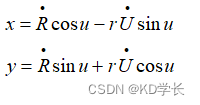
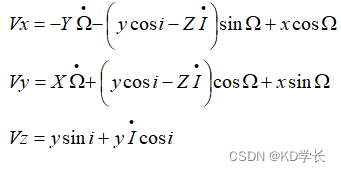
六、计算卫星钟偏

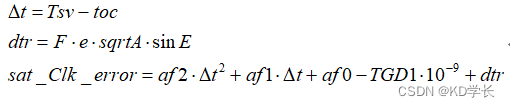
七、MATLAB代码&运行示例

主程序 main.m：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 计算BD卫星的位置和速度
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear;
clc;% 卫星发射时刻
tsv = 3.744000000000e+05 + 20;% MEO卫星的星历参数
MEO_eph.toc = 3.744000000000e+05;
MEO_eph.af2 = 0.000000000000e+00;
MEO_eph.af1 = -1.854782993860e-11;
MEO_eph.af0 = -1.551879104230e-04;
MEO_eph.TGD1 = -2.499999984810e-09;
MEO_eph.sqrtA = 6.493531814580e+03;
MEO_eph.toe = 3.744000000000e+05;
MEO_eph.deltan = 1.561493613910e-09;
MEO_eph.M0 = -2.192800555490e+00;
MEO_eph.e = 6.275521009230e-03;
MEO_eph.i0 = 9.618269834520e-01;
MEO_eph.IDOT = -7.286017777600e-11;
MEO_eph.omega = -2.286522345190e+00;
MEO_eph.Cuc = -1.096632331610e-06;
MEO_eph.Cus = 8.363742381330e-06;
MEO_eph.Crc = -8.421875000000e+00;
MEO_eph.Crs = -3.535937500000e+01;
MEO_eph.Cic = -2.700835466380e-08;
MEO_eph.Cis = 5.215406417850e-08;
MEO_eph.omega0 = 2.343958791130e+00;
MEO_eph.omegaDot = -1.925437345050e-09;% GEO卫星的星历参数
GEO_eph.toc = 3.744000000000e+05;
GEO_eph.af2 = 0.000000000000e+00;
GEO_eph.af1 = -6.030731469760e-11;
GEO_eph.af0 = 1.385881332680e-04;
GEO_eph.TGD1 = 2.999999970670e-10;
GEO_eph.sqrtA = 6.493444162370e+03;
GEO_eph.toe = 3.744000000000e+05;
GEO_eph.deltan = -5.663093033410e-09;
GEO_eph.M0 = -6.708219322780e-01;
GEO_eph.e = 7.320673903450e-04;
GEO_eph.i0 = 9.409420036110e-02;
GEO_eph.IDOT = 2.378670509750e-10;
GEO_eph.omega = -1.792511645600e+00;
GEO_eph.Cuc = -7.327646017070e-06;
GEO_eph.Cus = -1.202011480930e-05;
GEO_eph.Crc = 3.626718750000e+02;
GEO_eph.Crs = -2.278125000000e+02;
GEO_eph.Cic = -5.634501576420e-08;
GEO_eph.Cis = 3.259629011150e-08;
GEO_eph.omega0 = -6.255581541050e-01;
GEO_eph.omegaDot = 6.869929017260e-09;% 分别计算GEO、MEO卫星位置
[MEO_positionX, MEO_positionY, MEO_positionZ, MEO_Vx, MEO_Vy, MEO_Vz, MEO_sat_Clk_error] = MEO_state_tsv(tsv,MEO_eph);
[GEO_positionX, GEO_positionY, GEO_positionZ, GEO_sat_Clk_error] = GEO_state_tsv(tsv,GEO_eph);% 打印输出
fprintf('GEO卫星位置：[%f, %f, %f]\n',GEO_positionX,GEO_positionY,GEO_positionZ);
fprintf('GEO卫星钟偏：%f\n',GEO_sat_Clk_error);
fprintf('\n');
fprintf('MEO卫星位置：[%f, %f, %f]\n',MEO_positionX,MEO_positionY,MEO_positionZ);
fprintf('MEO卫星速度：[%f, %f, %f]\n',MEO_Vx,MEO_Vy,MEO_Vz);
fprintf('MEO卫星钟偏：%f\n',MEO_sat_Clk_error);

函数 MEO_state_tsv.m：

function [positionX,positionY,positionZ,Vx,Vy,Vz,sat_Clk_error] = MEO_state_tsv(tsv,EPH)
%计算MEO卫星的位置%%%%%%%%%%%%%%%%
%数据准备
%%%%%%%%%%%%%%%%
radv = 7.2921151467e-5;
GM = 3.986005e14;
F = -4.442807633e-10;
toc = EPH.toc;
Tsv = tsv;
af0 = EPH.af0;
af1 = EPH.af1;
af2 = EPH.af2;
TGD1 = EPH.TGD1;
sqrtA = EPH.sqrtA;
toe = EPH.toe;
deltan = EPH.deltan;
M0 = EPH.M0;
e = EPH.e;
i0 = EPH.i0;
IDOT = EPH.IDOT;
omega = EPH.omega;
Cuc = EPH.Cuc;
Cus = EPH.Cus;
Crc = EPH.Crc;
Crs = EPH.Crs;
Cic = EPH.Cic;
Cis = EPH.Cis;
omega0 = EPH.omega0;
omegaDot = EPH.omegaDot;%计算卫星信号发射时间
delt = Tsv - toc;
sat_Clk_error = af2*delt^2 + af1*delt + af0 - TGD1*1e-9;
Tsv = Tsv - sat_Clk_error;%计算规划时间
tk = Tsv - toe;%计算平近点角
a = sqrtA^2;
n = sqrt(GM/(a^3)) + deltan;
M = M0 + n*tk;
M = mod(M,2*pi);%迭代求解偏近点角
E0 = M;
while 1Ei = M + e*sin(E0);delt_E = Ei - E0;delt_E = rem(delt_E,2*pi);if abs(delt_E) < 1e-12E = Ei;break;elseE0 = Ei;end
end%求解真近点角和升交点角距
nu = atan2(sqrt(1-e^2)*sin(E),cos(E)-e);
phi = nu + omega;
phi = rem(phi,2*pi);%考虑摄动改正项
delt_u = Cuc*cos(2*phi) + Cus*sin(2*phi);
delt_r = Crc*cos(2*phi) + Crs*sin(2*phi);
delt_i = Cic*cos(2*phi) + Cis*sin(2*phi);
u = phi + delt_u;
r = a*(1-e*cos(E))+delt_r;
i = i0+IDOT*tk+delt_i;%计算升交点赤经
OMEGA = omega0+(omegaDot-radv)*tk-radv*toe;
OMEGA = mod(OMEGA,2*pi);%卫星坐标WGS-84
positionX = cos(u)*r*cos(OMEGA) - sin(u)*r*cos(i)*sin(OMEGA);
positionY = cos(u)*r*sin(OMEGA) + sin(u)*r*cos(i)*cos(OMEGA);
positionZ = sin(u)*r*sin(i);%计算卫星速度
E_dot = n/(1-e*cos(E));
Vk_dot = (sqrt(1-e^2)*E_dot)/(1-e*cos(E));Uk_dot = 2*Vk_dot*(Cus*cos(2*phi)-Cuc*sin(2*phi));
Rk_dot = 2*Vk_dot*(Crs*cos(2*phi)-Crc*sin(2*phi));
Ik_dot = 2*Vk_dot*(Cis*cos(2*phi)-Cic*sin(2*phi));U_dot = Vk_dot + Uk_dot;
R_dot = a*e*E_dot*sin(E) + Rk_dot;
I_dot = IDOT + Ik_dot;OMEGA_dot = omegaDot - radv;x = R_dot*cos(u) - r*U_dot*sin(u);
y = R_dot*sin(u) + r*U_dot*cos(u);Vx = -positionY*OMEGA_dot - (y*cos(i)-positionZ*I_dot)*sin(OMEGA) + x*cos(OMEGA);
Vy = positionX*OMEGA_dot + (y*cos(i)-positionZ*I_dot)*cos(OMEGA) + x*sin(OMEGA);
Vz = y*sin(i) + y*I_dot*cos(i);%更新卫星钟偏
dtr = F*e*sqrtA*sin(E);
sat_Clk_error = af2*delt^2 + af1*delt + af0 - TGD1*1e-9 + dtr;end

函数 GEO_state_tsv.m：

function [positionX,positionY,positionZ,sat_Clk_error] = GEO_state_tsv(tsv,EPH)
%计算GEO卫星的位置%%%%%%%%%%%%%%%%
%数据准备
%%%%%%%%%%%%%%%%
radv = 7.2921151467e-5;
GM = 3.986005e14;
F = -4.442807633e-10;
toc = EPH.toc;
Tsv = tsv;
af0 = EPH.af0;
af1 = EPH.af1;
af2 = EPH.af2;
TGD1 = EPH.TGD1;
sqrtA = EPH.sqrtA;
toe = EPH.toe;
deltan = EPH.deltan;
M0 = EPH.M0;
e = EPH.e;
i0 = EPH.i0;
IDOT = EPH.IDOT;
omega = EPH.omega;
Cuc = EPH.Cuc;
Cus = EPH.Cus;
Crc = EPH.Crc;
Crs = EPH.Crs;
Cic = EPH.Cic;
Cis = EPH.Cis;
omega0 = EPH.omega0;
omegaDot = EPH.omegaDot;%计算卫星信号发射时间
delt = Tsv - toc;
sat_Clk_error = af2*delt^2 + af1*delt + af0 - TGD1*1e-9;
Tsv = Tsv - sat_Clk_error;%计算规划时间
tk = Tsv - toe;%计算平近点角
a = sqrtA^2;
n = sqrt(GM/(a^3)) + deltan;
M = M0 + n*tk;
M = mod(M,2*pi);%迭代求解偏近点角
E0 = M;
while 1Ei = M + e*sin(E0);delt_E = Ei - E0;delt_E = rem(delt_E,2*pi);if abs(delt_E) < 1e-12E = Ei;break;elseE0 = Ei;end
end%求解真近点角和升交点角距
nu = atan2(sqrt(1-e^2)*sin(E),cos(E)-e);
phi = nu + omega;
phi = rem(phi,2*pi);%考虑摄动改正项
delt_u = Cuc*cos(2*phi) + Cus*sin(2*phi);
delt_r = Crc*cos(2*phi) + Crs*sin(2*phi);
delt_i = Cic*cos(2*phi) + Cis*sin(2*phi);
u = phi + delt_u;
r = a*(1-e*cos(E))+delt_r;
i = i0+IDOT*tk+delt_i;%计算升交点赤经
OMEGA = omega0+omegaDot*tk-radv*toe;
OMEGA = mod(OMEGA,2*pi);%卫星坐标WGS-84
X = cos(u)*r*cos(OMEGA) - sin(u)*r*cos(i)*sin(OMEGA);
Y = cos(u)*r*sin(OMEGA) + sin(u)*r*cos(i)*cos(OMEGA);
Z = sin(u)*r*sin(i);%GEO卫星的位置
f = -5/180*pi;
p = radv*tk;
Rx = [1 0 0; 0 cos(f) sin(f); 0 -sin(f) cos(f)];
Rz = [cos(p) sin(p) 0; -sin(p) cos(p) 0; 0 0 1];
position = Rz*Rx*[X;Y;Z];
positionX = position(1);
positionY = position(2);
positionZ = position(3);%更新卫星钟偏
dtr = F*e*sqrtA*sin(E);
sat_Clk_error = af2*delt^2 + af1*delt + af0 - TGD1*1e-9 + dtr;end

运行结果：

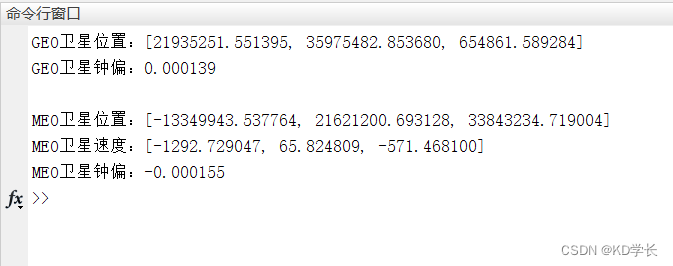
这篇关于利用北斗BDS广播星历，进行卫星位置计算的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/844869。

相关文章

Python中经纬度距离计算的实现方式

Python中经纬度距离计算的实现方式

《Python中经纬度距离计算的实现方式》文章介绍Python中计算经纬度距离的方法及中国加密坐标系转换工具,主要方法包括geopy（Vincenty/Karney）、Haversine、pyproj... 目录一、基本方法1. 使用geopy库（推荐）2. 手动实现 Haversine 公式3. 使用py
阅读更多...
MySQL进行分片合并的实现步骤

MySQL进行分片合并的实现步骤

《MySQL进行分片合并的实现步骤》分片合并是指在分布式数据库系统中,将不同分片上的查询结果进行整合,以获得完整的查询结果,下面就来具体介绍一下,感兴趣的可以了解一下... 目录环境准备项目依赖数据源配置分片上下文分片查询和合并代码实现1. 查询单条记录2. 跨分片查询和合并测试结论分片合并（Shardin
阅读更多...
SpringBoot结合Knife4j进行API分组授权管理配置详解

SpringBoot结合Knife4j进行API分组授权管理配置详解

《SpringBoot结合Knife4j进行API分组授权管理配置详解》在现代的微服务架构中,API文档和授权管理是不可或缺的一部分,本文将介绍如何在SpringBoot应用中集成Knife4j,并进... 目录环境准备配置 Swagger配置 Swagger OpenAPI自定义 Swagger UI 底
阅读更多...
基于Python Playwright进行前端性能测试的脚本实现

基于Python Playwright进行前端性能测试的脚本实现

《基于PythonPlaywright进行前端性能测试的脚本实现》在当今Web应用开发中,性能优化是提升用户体验的关键因素之一,本文将介绍如何使用Playwright构建一个自动化性能测试工具,希望... 目录引言工具概述整体架构核心实现解析1. 浏览器初始化2. 性能数据收集3. 资源分析4. 关键性能指
阅读更多...
Nginx进行平滑升级的实战指南(不中断服务版本更新)

Nginx进行平滑升级的实战指南(不中断服务版本更新)

《Nginx进行平滑升级的实战指南(不中断服务版本更新)》Nginx的平滑升级（也称为热升级）是一种在不停止服务的情况下更新Nginx版本或添加模块的方法,这种升级方式确保了服务的高可用性,避免了因升... 目录一.下载并编译新版Nginx1.下载解压2.编译二.替换可执行文件，并平滑升级1.替换可执行文件
阅读更多...
Python进行JSON和Excel文件转换处理指南

Python进行JSON和Excel文件转换处理指南

《Python进行JSON和Excel文件转换处理指南》在数据交换与系统集成中,JSON与Excel是两种极为常见的数据格式,本文将介绍如何使用Python实现将JSON转换为格式化的Excel文件,... 目录将 jsON 导入为格式化 Excel将 Excel 导出为结构化 JSON处理嵌套 JSON：
阅读更多...
一文解密Python进行监控进程的黑科技

一文解密Python进行监控进程的黑科技

《一文解密Python进行监控进程的黑科技》在计算机系统管理和应用性能优化中,监控进程的CPU、内存和IO使用率是非常重要的任务,下面我们就来讲讲如何Python写一个简单使用的监控进程的工具吧... 目录准备工作监控CPU使用率监控内存使用率监控IO使用率小工具代码整合在计算机系统管理和应用性能优化中，监
阅读更多...
如何使用Lombok进行spring 注入

如何使用Lombok进行spring 注入

《如何使用Lombok进行spring注入》本文介绍如何用Lombok简化Spring注入,推荐优先使用setter注入,通过注解自动生成getter/setter及构造器,减少冗余代码,提升开发效... Lombok为了开发环境简化代码，好处不用多说。spring 注入方式为2种，构造器注入和setter
阅读更多...
MySQL进行数据库审计的详细步骤和示例代码

MySQL进行数据库审计的详细步骤和示例代码

《MySQL进行数据库审计的详细步骤和示例代码》数据库审计通过触发器、内置功能及第三方工具记录和监控数据库活动,确保安全、完整与合规,Java代码实现自动化日志记录,整合分析系统提升监控效率,本文给大... 目录一、数据库审计的基本概念二、使用触发器进行数据库审计1. 创建审计表2. 创建触发器三、Java
阅读更多...
MySQL深分页进行性能优化的常见方法

MySQL深分页进行性能优化的常见方法

《MySQL深分页进行性能优化的常见方法》在Web应用中,分页查询是数据库操作中的常见需求,然而,在面对大型数据集时,深分页（deeppagination）却成为了性能优化的一个挑战,在本文中,我们将... 目录引言：深分页，真的只是“翻页慢”那么简单吗？一、背景介绍二、深分页的性能问题三、业务场景分析四、
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2