本文主要是介绍2024牛客寒假算法基础集训营4补题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
E:贪心+数据结构

首先,我们看一个例子:
114514,令k=3,我们从左开始,1,1,4,此时为3的倍数,那么我们就截断。
因为若我们在此截断,后面的5会对以后的数产生有利的影响(大不了忽略)。
因此,我们在从5开始,一旦发现有为3倍数的子区间就停,那么我们如何判断?
提供一个极为巧妙地方法,我们记录前缀和,然后mod3,如果加进来有两个值相等,因为sum是递增的,我们就可以判断出它有3的倍数,这样我们用DP维护即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,k,a[200010],cnt,ww[200010],sum[200010];
map<int,int> mp;
int main(){cin>>n>>k;for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) sum[i]=(sum[i-1]+a[i])%k;for(int i=1;i<=n;i++) ww[i]=sum[i]%k;mp[0]=1;for(int i=1;i<=n;i++){if(mp.count(ww[i])==0) mp[ww[i]]=1;else{mp.clear();cnt++;mp[ww[i]]=1;}}cout<<cnt; }F.DP

十分的巧妙:
我们令f[i]表示前i个数选6个的最大分数,易得状态转移方程:f[i]=max(f[i],dp[j][i]+f[j-1])(其中dp[i][j]表示i---j中选6个的最大值,那么我们如何求?
我们令dpmax[i][j]表示前i个数(有左界)选j个数式子的最大值。
易得j==1时,dpmax[i][j]=max(dpmax[i-1][j],a[i])
当k=2/4/6时,dpmax[i][j]=max(dpmax[i-1][j],dpmax[i-1][j-1]-a[i])
当k=3/5时,我们还要维护一下min,因为负数*负数可能得到一个最大值。
dpmax[i][j]=max(max(dpmax[i-1][j],dpmax[j-1][j-1]*a[i]),dpmin[j-1][j-1]*a[i]).
同时我们保证区间里数的个数>=k即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
int n,a[1010],dp[1010][1010],f[1010];
int main(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];memset(f,0x80,sizeof(f));for(int i=1;i<=n;i++){int dpmax[1010][7],dpmin[1010][7];memset(dpmax,0x80,sizeof(dpmax));memset(dpmin,0x7f,sizeof(dpmin));for(int j=i;j<=n;j++){for(int k=1;k<=6;k++){if(k==1){dpmax[j][1]=max(a[j],dpmax[j-1][1]);dpmin[j][1]=min(dpmin[j-1][1],a[j]);}else if(k==2||k==4||k==6){if(j-i+1>=k){dpmax[j][k]=max(dpmax[j-1][k],dpmax[j-1][k-1]-a[j]);dpmin[j][k]=min(dpmin[j-1][k],dpmin[j-1][k-1]-a[j]);}}else{if(j-i+1>=k){dpmax[j][k]=max(max(dpmax[j-1][k],dpmax[j-1][k-1]*a[j]),dpmin[j-1][k-1]*a[j]);dpmin[j][k]=min(min(dpmin[j-1][k],dpmin[j-1][k-1]*a[j]),dpmax[j-1][k-1]*a[j]);}}}dp[i][j]=max(dp[i][j],dpmax[j][6]);}}f[0]=0;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){f[i]=max(f[i],f[j-1]+dp[j][i]);}}cout<<f[n];
}G.暴力枚举:

我们先枚举顶点,然后我们往依次下看,用前缀和看看当前层的左右端点的里面是否满即可。
下面是AC代码:
#include<bits/stdc++.h>
using namespace std;
char a[510][510],x;
int n,m,sum[510][510];
int main(){cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>x;a[i][j]=x;}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){sum[i][j]=sum[i][j-1]+(a[i][j]=='*');}}long long cnt=0;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(a[i][j]=='*'){int c=i+1,l=j-1,r=j+1;while(c<=n&&l>=1&&r<=m&&a[c][l]=='*'&&a[c][r] == '*'){if(sum[c][r]-sum[c][l-1]==r-l+1) cnt++;c++;l--;r++;}}}}cout<<cnt;
}I.最短路(带路径修改的Dijkstra)(喵喵喵):
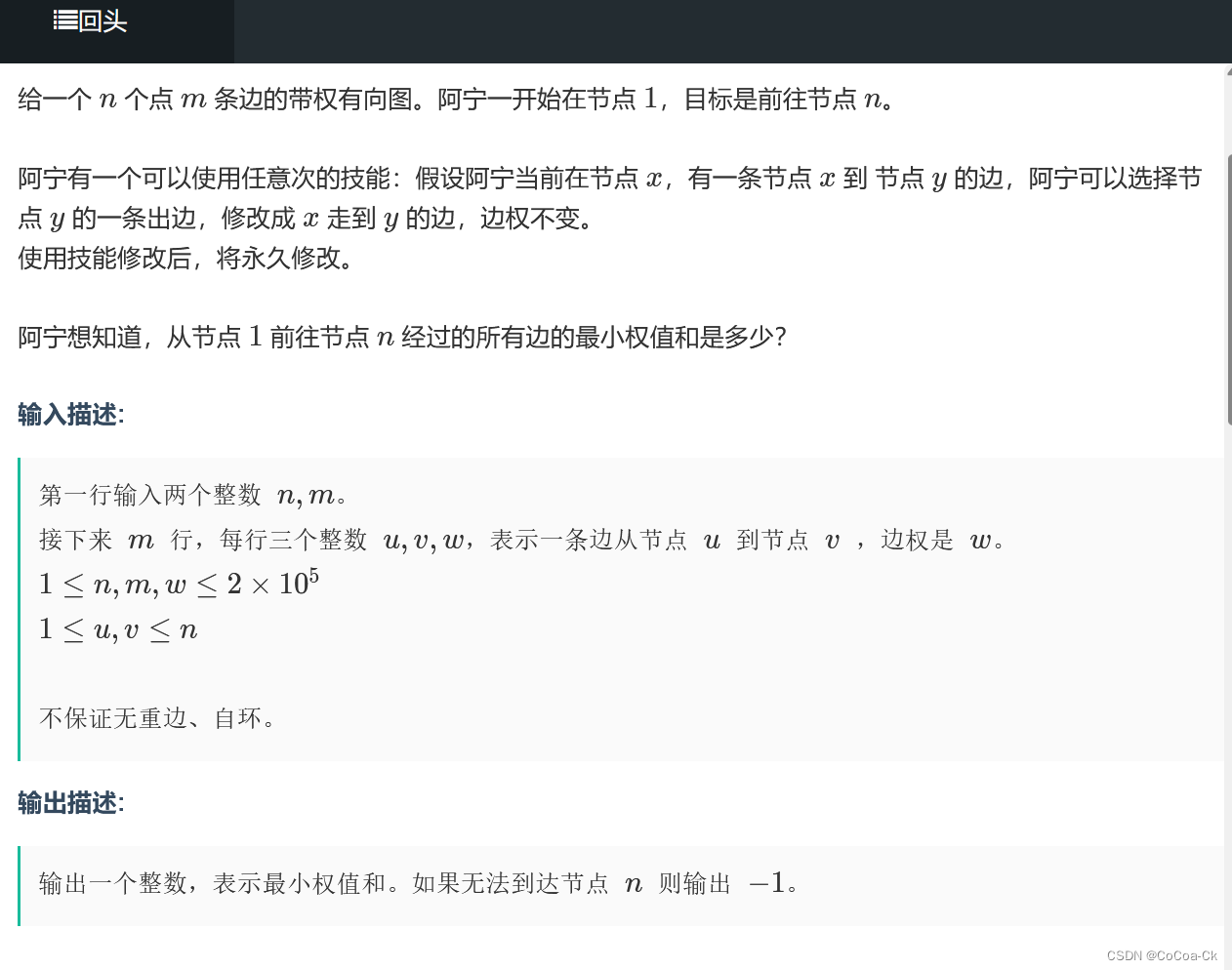
相比于普通的迪杰斯特拉,我们只需要增加反悔操作,我们在普通dis上再开一维,0表示没有欠了(即没有选正常的路,需要技能去填补),1表示欠了一次(不能欠的更多了)。当我们到了有0的位置,它的位置没有欠,我们根据这个再推出下一个的0/1即可。
当我们到了1,首先我们要判断到y的那条边是否是最短的那条,然后就是用除了它的第一小边去填补即可。
下面是官方题解代码(喵喵喵):
#include <bits/stdc++.h>
using namespace std;
#define LL long long
using PII = pair<int, int>;
const int N = 3 + 2e5;
struct Node {LL d;int x, z;bool operator<(const Node& other) const { return d > other.d; }
};
int n, m;
vector<PII> edge[N];
vector<int> idx[N];
LL d[N][2];
bool vis[N][2];
priority_queue<Node> q;
void update(int y,int z,long long v){//z=0/1,y为到的点 if(d[y][z]>v){d[y][z] = v;q.push({d[y][z], y, z});}
}
int main() {cin >> n >> m;while (m--) {int u, v, w;cin >> u >> v >> w;edge[u].push_back({v, w});}for (int i = 1; i <= n; ++i) {idx[i].resize(edge[i].size());for (int j = 0; j < idx[i].size(); ++j) {idx[i][j] = j;}sort(idx[i].begin(), idx[i].end(), [&](const int& a, const int& b) {return edge[i][a].second < edge[i][b].second;});while (idx[i].size() > 2) {// 操作时,如果走的不是最短的,那肯定操作最短的边// 如果走的是最短的,那肯定操作次短的边// 因此可以只最短保留2条边idx[i].pop_back();}}memset(d, 0x3f, sizeof(d));update(1, 0, 0); // 在起点肯定没有欠while (!q.empty()) {auto [dd, x, z] = q.top();/*和以下代码一样效果:auto node = q.top();LL dd = node.d;int x = node.x;int z = node.z;*/q.pop();if (vis[x][z]) {continue;}vis[x][z] = 1;if (z == 0) {// 来到 x不欠费for (int i = 0; i < edge[x].size(); ++i) {auto [y, w] = edge[x][i];/*和以下代码一样效果:auto e = edge[x][i];int y = e.first, w = e.second;*/update(y, 0, d[x][0] + w);update(y, 1, d[x][0]);}} else {// 来到 x 欠费if (idx[x].size() == 2) {// 前面操作成只保留最短的两条边// 没有idx[x].size() == 1,因为这个情况是走回去,没必要判// 而且对于下面代码会越界for (int i = 0; i < edge[x].size(); ++i) {auto [y, w] = edge[x][i];if (i != idx[x][0]) {// 走去y不是idx[x][0]这最短边// 拿idx[x][0]抵消欠费// 不欠费走到 yupdate(y, 0, d[x][1] + w + edge[x][idx[x][0]].second);// 欠费走到 yupdate(y, 1, d[x][1] + edge[x][idx[x][0]].second);} else {// 走去y是idx[x][0]这最短边// 拿idx[x][1]次短边,抵消欠费// 不欠费走到 yupdate(y, 0, d[x][1] + w + edge[x][idx[x][1]].second);// 欠费走到 yupdate(y, 1, d[x][1] + edge[x][idx[x][1]].second);}}}}}LL ans = d[n][0];if (idx[n].size() >= 1) {// 终点,该把费用清一下ans = min(ans, d[n][1] + edge[n][idx[n][0]].second);}if (ans > 1e18) { // 没有答案ans = -1;}cout << ans << endl;return 0;
}其中有几点注意的:
1.用pair+vector来存带权图。
2.注意预先处理出每一个点引出的最小的两条边。
这篇关于2024牛客寒假算法基础集训营4补题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





