数据结构面试常见问题之串的模式匹配(KMP算法)系列-大师改进

本文主要是介绍数据结构面试常见问题之串的模式匹配(KMP算法)系列-大师改进，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

😀前言
KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）

KMP算法的优势:

提高了匹配效率，时间复杂度为O(m+n)，其中m为模式串长度，n为主串长度。
克服了朴素算法的回溯问题，减少了不必要的比较次数。

🏠个人主页：尘觉主页

数据结构面试常见问题之串的模式匹配(KMP算法)系列-大师改进

KMP-2. KMP 算法思路

大师改进

方法3：KMP(Knuth、Morris、Pratt)算法

T = O(n+m)
简单的往前错一位的比较是完全没有必要的没有意义的，如下图

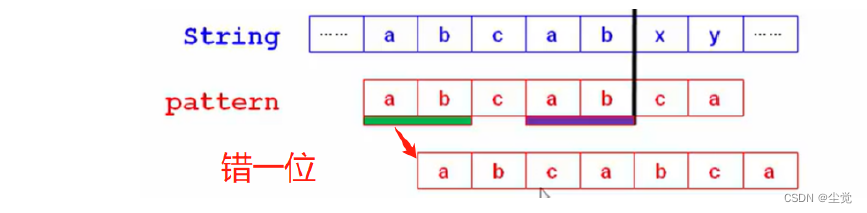
KMP算法的想法：

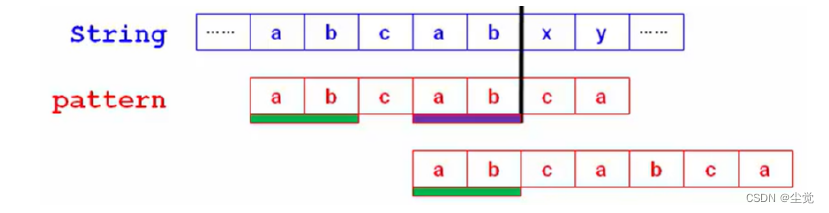
指针指向x不会回退(回溯)了，直接继续从x开始，继续往前比较

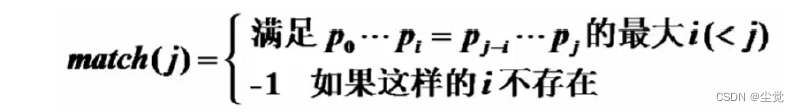
match的具体例子

下标从0到9
第0个字符对应的是一个长度为1的子串，所以他不可能产生匹配，match就永远是-1
从0到1：a跟b是配不上的，match也为-1
0-2：a和c配不上，ab和bc也配不上，所以match还是为-1
0-3：ab和ca是配不上的，abc跟bca也配不上，a对应的j为0，所以match也为0
//此时限制条件是最大i是小于j的，如果i=j的话那就相当于自己等于自己就没有意义了(p0...pj =p0...pj)
//所以我们考虑他的真子串
0-4：a跟b配不上，abc跟cab配不上，ab跟ab能配上，match值为1...

对于 pattern = abcabcacab，最后 3 个字符的 match 值是多少？-1, 0, 1
在早期的教科书上被叫做failure(失败的意思)

match值的含义：
例子：从0到6的子串，首跟尾能配上的小串，从0开始他的尾部下标为3，abca跟abca能配上。这就是match的含义

此代码块内容来自百度百科：
KMP算法是一种改进的字符串匹配算法，由D.E.Knuth，J.H.Morris和V.R.Pratt提出的，因此人们称它为克努特—莫里斯—普拉特操作（简称KMP算法）。KMP算法的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个next()函数实现，函数本身包含了模式串的局部匹配信息。KMP算法的时间复杂度O(m+n)
KMP算法是三位学者在 Brute-Force算法的基础上同时提出的模式匹配的改进算法。Brute- Force算法在模式串中有多个字符和主串中的若干个连续字符比较都相等,但最后一个字符比较不相等时,主串的比较位置需要回退。KMP算法在上述情况下,主串位置不需要回退,从而可以大大提高效率

模式匹配类型

(1)精确匹配
如果在目标T中至少一处存在模式P，则称匹配成功，否则即使目标与模式只有一个字符不同也不能称为匹配成功，即匹配失败。给定一个字符或符号组成的字符串目标对象T和一个字符串模式P，模式匹配的目的是在目标T中搜索与模式P完全相同的子串,返回T和P匹配的第一个字符串的首字母位置 。
(2)近似匹配
如果模式P与目标T(或其子串)存在某种程度的相似,则认为匹配成功。常用的衡量字符串相似度的方法是根据一个串转换成另一个串所需的基本操作数目来确定。基本操作由字符串的插入、删除和替换来组成

第一篇–>数据结构面试常见问题之串的模式匹配(KMP算法)系列-简单解决方案

第二篇–>数据结构面试常见问题之串的模式匹配(KMP算法)系列-大师改进

第三篇–>数据结构面试常见问题之串的模式匹配(KMP算法)系列-大师改进实现以及原理

😄总结

KMP算法思路

KMP算法的核心思想是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数。具体来说，KMP算法通过一个next数组记录模式串的部分匹配信息，当主串与模式串匹配失败时，可以根据next数组直接跳转到模式串中下一个可能匹配的位置，避免回溯。

next数组的含义:

next[j]表示模式串P的前j个字符(不包括第j个字符)与P的后缀中最长的公共前缀的长度。

举个例子:

模式串P = “ABCDABD”

next[0] = -1 (空串与任何字符串都没有公共前缀)

next[1] = 0 (A与空串的公共前缀是空串)

next[2] = 0 (AB与A的公共前缀是A)

next[3] = 1 (ABC与AB的公共前缀是AB)

next[4] = 2 (ABCD与ABC的公共前缀是ABC)

next[5] = 3 (ABCDAB与ABCD的公共前缀是ABCD)

next[6] = 2 (ABCDABD与ABCDAB的公共前缀是ABCDAB)

大师改进：KMP算法

KMP算法的核心改进在于next数组的计算。朴素的next数组计算方法是逐个计算每个next[j]的值，时间复杂度为O(m^2)。KMP算法通过改进next数组的计算方法，将时间复杂度降低到O(m)。

改进后的next数组计算方法:

初始化next[0] = -1
从j = 1开始循环
若P[j] = P[next[j-1]]，则next[j] = next[j-1] + 1
若P[j] != P[next[j-1]]，则
若next[j-1] != -1，则令j = next[j-1]，并重复步骤3
若next[j-1] == -1，则next[j] = 0

总结

KMP算法是字符串匹配领域的重要算法，具有广泛的应用价值。KMP算法的核心思想是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数，从而提高匹配效率。

😁热门专栏推荐
想学习vue的可以看看这个

java基础合集

数据库合集

redis合集

nginx合集

linux合集

手写机制

微服务组件

spring_尘觉

springMVC

mybits

等等等还有许多优秀的合集在主页等着大家的光顾感谢大家的支持

🤔欢迎大家加入我的社区 尘觉社区

文章到这里就结束了，如果有什么疑问的地方请指出，诸佬们一起来评论区一起讨论😁
希望能和诸佬们一起努力，今后我们一起观看感谢您的阅读🍻
如果帮助到您不妨3连支持一下，创造不易您们的支持是我的动力🤞

这篇关于数据结构面试常见问题之串的模式匹配(KMP算法)系列-大师改进的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---