行测小技巧

1. 前推后还是后推前？

• 前推后：
  如果……那么……
  只要……就……
  凡是……都……
  为了……一定……
  必然/必须/不能不
  意味着/说明了/关键是
• 后推前：
  只有……才……
  ……是……必不可少的
  ……是……必须的
  ……是……的必要前提
  除非……，否则不……
  不……，不……

2. 鲁滨逊定理

$A\to B⟺-A$ 或 $B$
例子：不吃饭就得饿死 = 吃饭或者饿死；你不走，我就走 = 你走或我走。
因为除非 $A$ 否则 $B$ 等于 $-A\to B$，所以除非 $A$ 否则 $B$ 也等价于 $A$ 或 $B$。

3. 从弱原则

原理：语气过于强硬的、过于绝对的，往往是错误的，而语气越弱的，往往越难以证明是错误的。

• 语气强：
  最 唯一 首要 越……越 比……更 决定 一定 所有都 一直/总是
• 语气弱：
  影响 可能 有的/某个/某种 有时候

适用题目：凡是要求“能推出”、“据此可知”等从题目中得出一个结论的题目，都应该第一时间想到从弱原则。在言语的细节判断题、逻辑的日常推理，甚至资料分析中，都能用到。

4. 凑整平衡思想

数学计算

5. 加强削弱秒杀十三技

• 只要是从一个事物推测另一个事物，就选两者相似或者不相似；
• 只要是从部分推整体、个别推普遍，就选样本典型或者不典型；
• 只要是对比试验，就看初始条件是否相同和变量是否唯一；
• 只要是观点得出很突兀，就选搭桥、做出解释；
• 只要是直接针对论点，就选；
• 只要是截然相反的否定，就选；
• 只要是否定前提，就选；
• 只要是题目涉及数字，就选带数字的选项；
• 只要是推出型观点让找削弱，就直接找 $A$ 且 $-B$；
• 只要是因果类加强，就选排除他因或没因没果；
• 只要是因果类削弱，就选因果倒置和另有他因；
• 只要是因果类涉及正反两方，就选根本原因；
• 只要是在其他选项的基础上，退一步还能加强或者削弱的，就选。

6. 反向代入法

适用情况：求增长量，选项非常接近。

7. 72法则

数学计算（增长率）

8. 自由度思想

原理：题干中，涉及到多个元素，然后给出若干条件，这些条件对不同的元素限制程度是不一样的，限制越少的，自由度越高，可能性越大。

9. 插板法

排列组合

10. 等价排除

11. 尾数法

12. 模态命题

几组等价公式：

• 不必然、不一定 = 可能不
• 不可能 = 必然不、一定不
• 并非所有都 = 有的不
• 并非有的 = 所有都不
• 并非有时候 = 一直都不，从来不
• 并非一直 = 有时候不
  

13. 增长量的比较

• 量大率大，增长量大；
• 在率差不多的情况，看量；
• 在量差不多的情况，看率；
• 量大率小的情况下，看两者乘积。

14. 二难推理

若 $A\to B$ 且 $-A\to B$，则 $B$ 为真；
若 $A\to B$ 且 $A\to -B$，则 $A$ 为假。

15. 变化率近似公式

如果 $B$ 和 $C$ 的增长率很小，则

• 若 $A=B\times C$，则 $r_a\approx r_b+r_c$
• 若 $A=\frac{B}{C}$，则 $r_a\approx r_b-r_c$

16. 插值法

17. 数字特性法

奇偶性：

• 加减规则：奇数 +/- 奇数 = 偶数 奇数 +/- 偶数 = 奇数 偶数 +/- 偶数 = 偶数
• 乘法规则：奇数 $\times$ 奇数 = 偶数 奇数 $\times$ 偶数 = 偶数 偶数 $\times$ 偶数 = 偶数

倍数特性：

• 整除特性
• 可传递性
• 可加减性
  

18. 增长率与二项式定理

$$A(1+r{)}^n=B$$
$$\frac{B}{A}=(1+r{)}^n=1+{\mathrm{C}}_{\mathrm{n}}^1\mathrm{r}+{\mathrm{C}}_{\mathrm{n}}2{\mathrm{r}}^2+\cdots \approx 1+\mathrm{nr}$$

19. 比重差公式

$$\frac{A}{B}-\frac{A}{B}\times \frac{1+r_b}{1+r_a}=\frac{A}{B}\frac{r_a-r_b}{1+r_a}$$

20. 跳坑原则

原理：

1. 有的题目题干晦涩难懂，但是选项非常简单；
2. 有的选项对题目中的概念具有解释作用；
3. 有的题干给出若干定义，真正需要精读细读的往往只有一个。

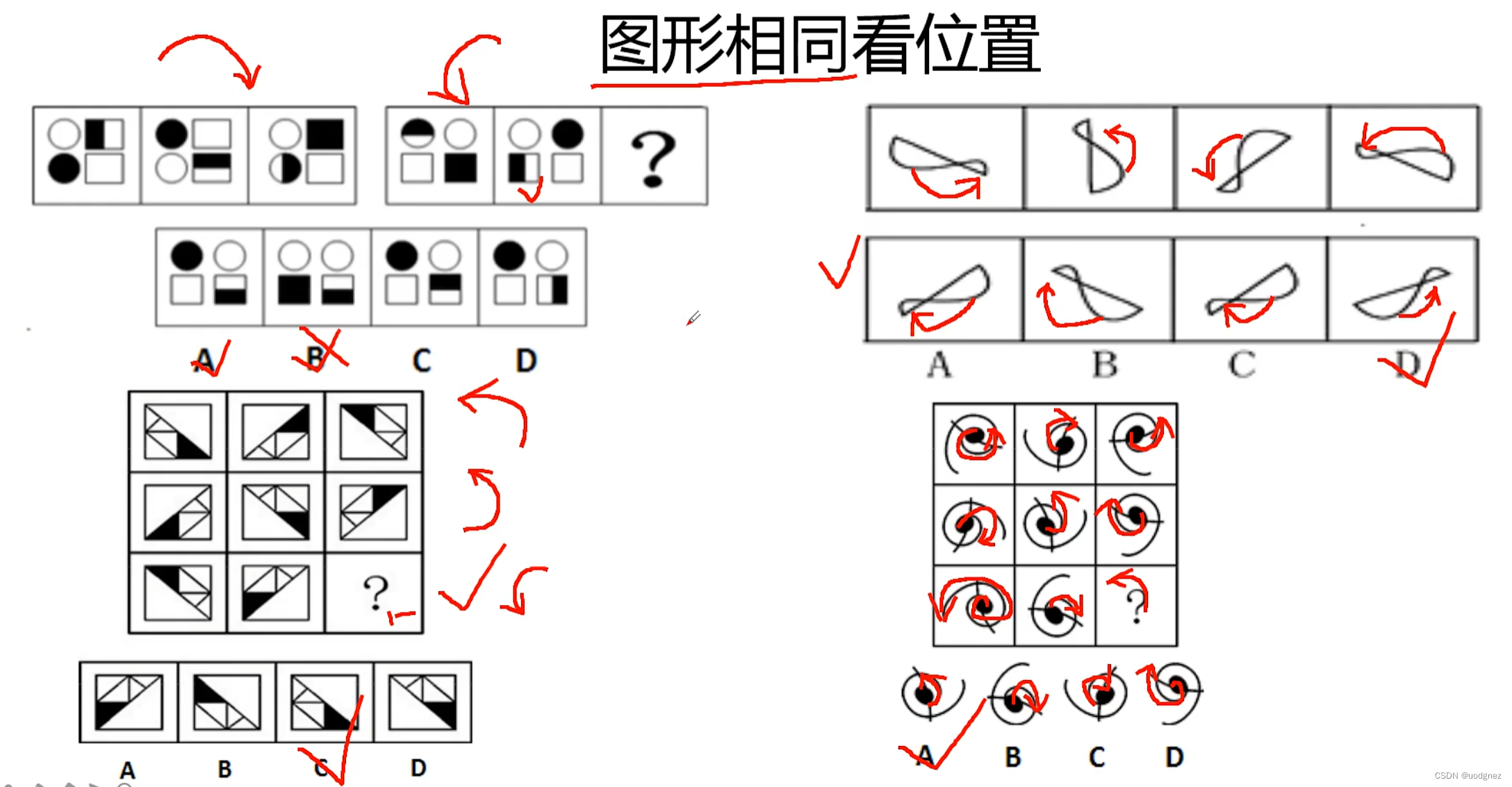
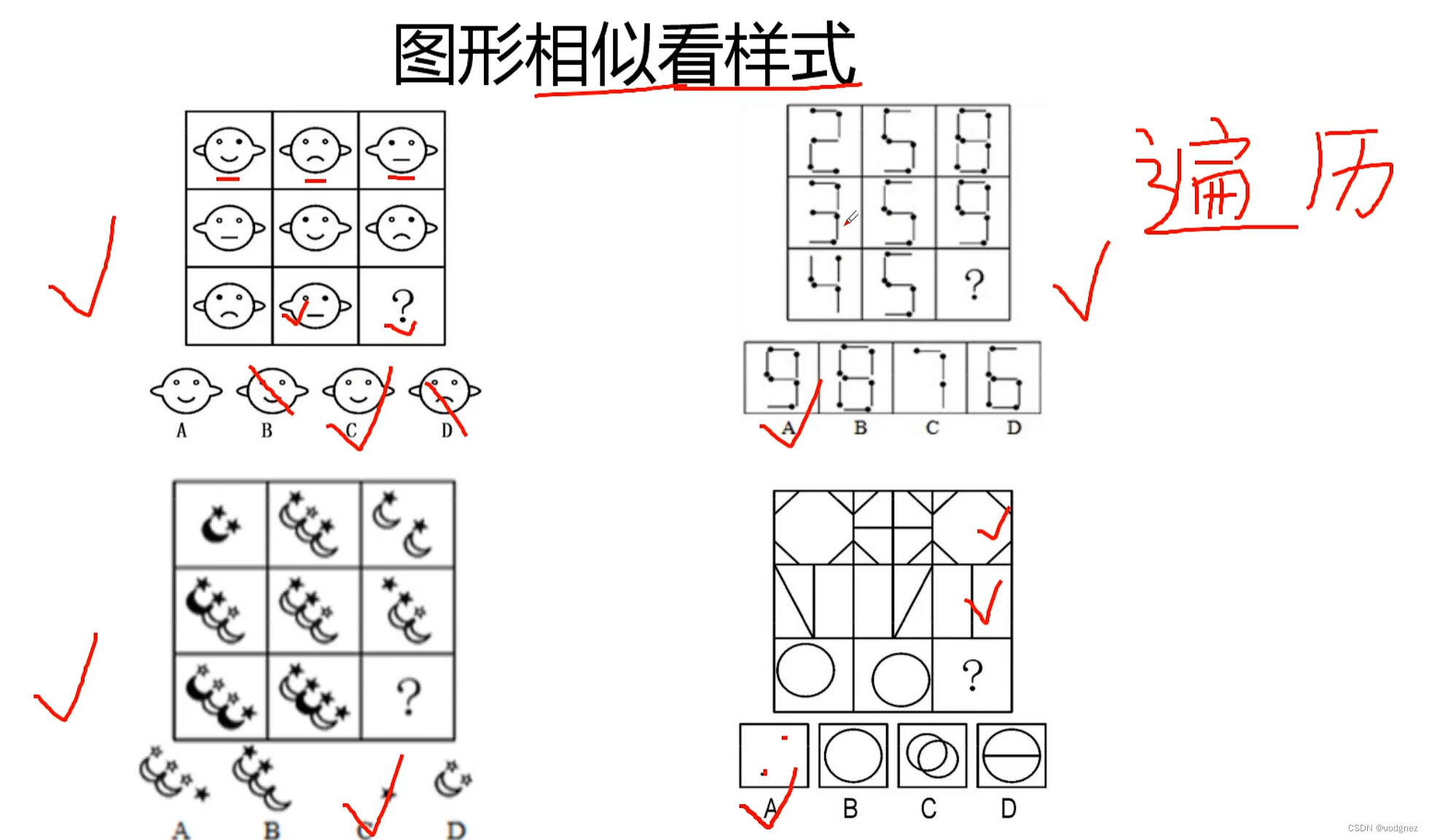
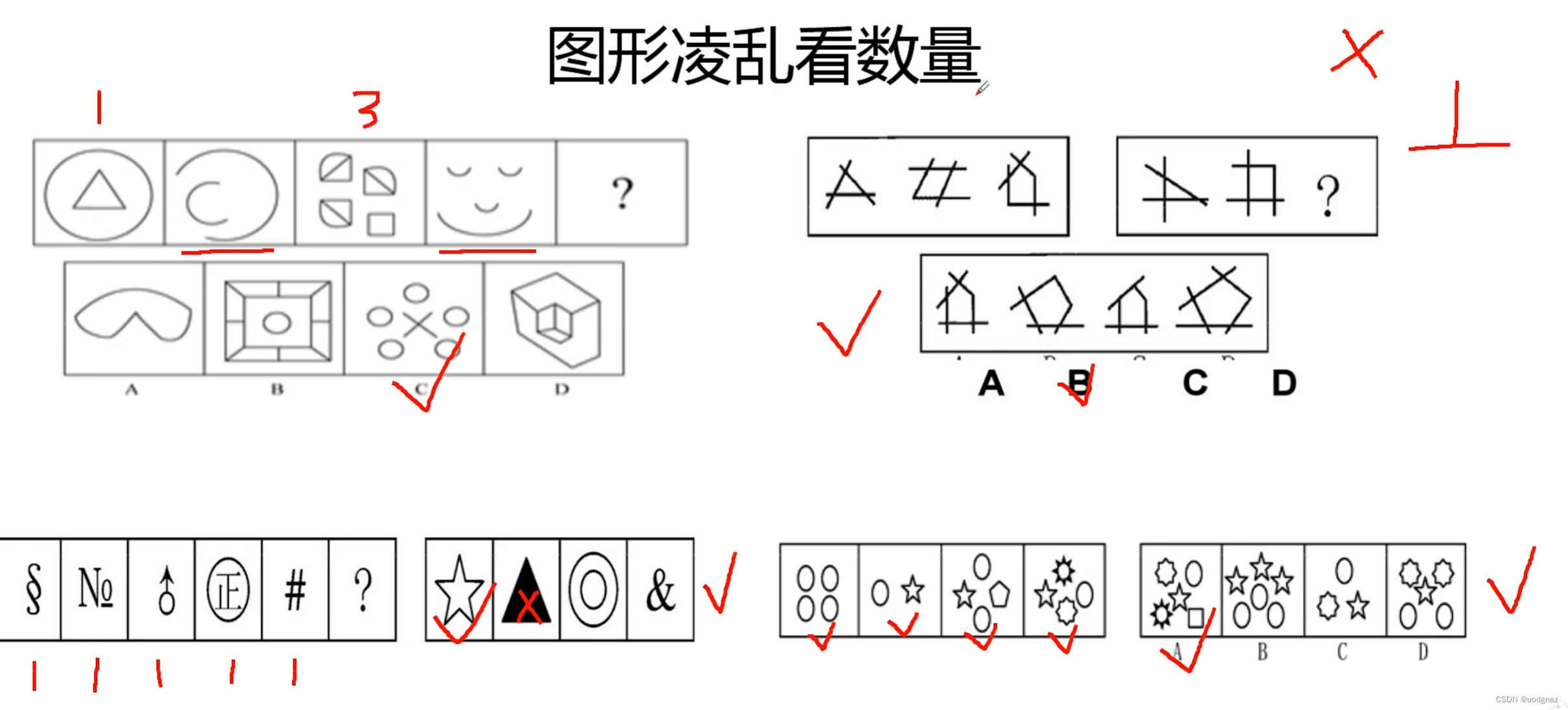
21. 平面图形推理三句口诀

图形相同看位置，图形相似看样式，图形凌乱看数量。

22. 一笔画看奇点个数

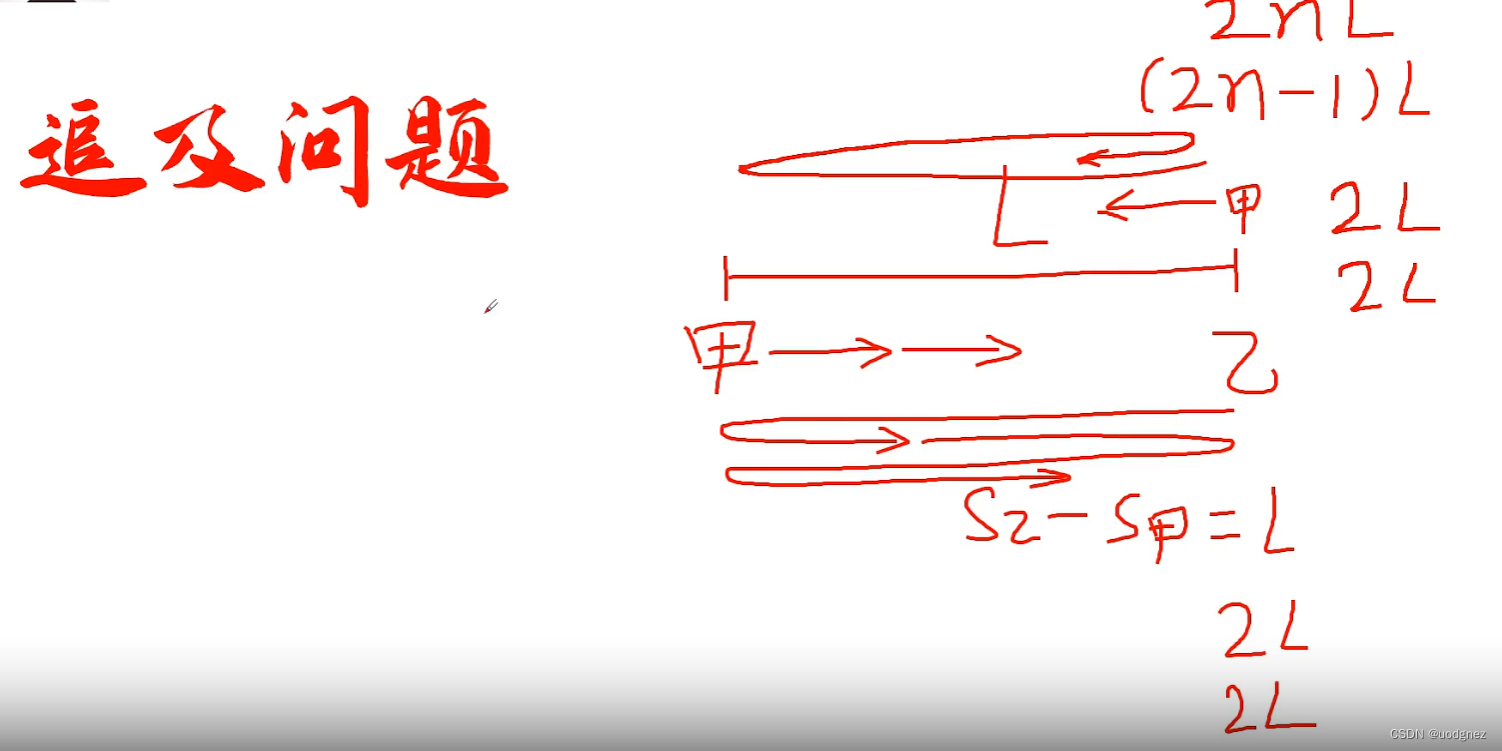
23. 多次相遇追及

24. 三集合容斥

画图

25. 牛吃草问题

26. 环排与错位重排

环排：$(n-1)!$

错位重排：$D_n=(n-1)(D_{n-1}+D_{n-2}),n>2$
$D_1=0,D_2=1,D_3=2,D_4=9,D_5=44$

27. 等距离平均速度

$$\frac{2v_1{v}_2}{v_1+v_2}$$

28.

来源于公考猫哥，仅供参考！