【Py/Java/C++三种语言OD2023C卷真题】20天拿下华为OD笔试之【模拟】2023C-攀登者2【欧弟算法】全网注释最详细分类最全的华为OD真题题解

2024-03-20 03:28
文章标签 java 算法 c++ 全网 笔试 模拟 三种 华为 py 真题 注释 20 题解 最全 od 拿下 欧弟 od2023c 2023c 攀登者

本文主要是介绍【Py/Java/C++三种语言OD2023C卷真题】20天拿下华为OD笔试之【模拟】2023C-攀登者2【欧弟算法】全网注释最详细分类最全的华为OD真题题解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

有LeetCode算法/华为OD考试扣扣交流群可加 948025485
可上全网独家的 欧弟OJ系统 练习华子OD、大厂真题
绿色聊天软件戳 od1336了解算法冲刺训练

文章目录

  • 题目描述与示例
    • 题目描述
      • 输入描述
      • 输出描述
    • 示例
      • 输入
      • 输出
  • 解题思路
    • 原路返回和非原路返回
    • 原路返回走过的总路程
    • 从左边空地出发原路返回
      • 寻找空地
      • 向右登山
      • 构建函数
    • 从右边空地出发原路返回
    • *为什么一定是原路返回（严谨证明）
  • 代码
    • python
    • java
    • cpp
    • 时空复杂度
  • 华为OD算法/大厂面试高频题算法练习冲刺训练

题目描述与示例

题目描述

攀登者喜欢寻找各种地图，并且尝试攀登到最高的山峰。

地图表示为一维数组，数组的索引代表水平位置，数组的高度代表相对海拔高度。其中数组元素 0 代表地面。

例如[0,1,2,4,3,1,0,0,1,2,3,1,2,1,0]， 代表如下图所示的地图。，地图中有两个山脉位置分别为 1,2,3,4,5和8,9,10,11,12,13，最高峰高度分别为4,3。最高峰位置分别为3,10。

一个山脉可能有多座山峰（高度大于相邻位置的高度，或在地图边界且高度大于相邻的高度）。

                4+---+|   ||   | 3                       3|   ||   +---+                   -----|       |                   |   |2 |       |                 2 |   |     2|       |                   |   |+---+       |               ----+   |   +---+|           |               |       |   |   |1 |           | 1           1 |       | 1 |   | 1|           |               |       |   |   |+---+           +---+       +---+       +---+   +---+|                   |       |                       |0 |                   | 0   0 |                       | 0|                   |       |                       |+---+                   +-------+                       +---+0   1   2   3   4   5   6   7   8   9  10  11  12  13  14

登山时会消耗登山者的体力（整数），上坡时，消耗相邻高度差两倍的体力，下坡时消耗相邻高度差一倍的体力，平地不消耗体力，登山者体力消耗到零时会有生命危险。

例如，上图所示的山峰：从索引 0，走到索引 1，高度差为 1，需要消耗 2*1=2 的体力；从索引 2 高度 2走到高度 4 索引 3 需要消耗 2*2=4 的体力；从索引 3 走到索引 4 则消耗 1*1=1 的体力。

攀登者想要评估一张地图内有多少座山峰可以进行攀登，且可以安全返回到地面，且无生命危险。

例如上图中的教组，有3个不同的山峰，登上位置在3的山可以从位置0或者位置6开始，从位置0登到山顶需要消耗体力1*2+1*2+2*2=8，从山顶返回到地面0需要消耗体力 2*1+1*1+1*1=4的体力，按照登山路线0->3->0需要消耗体力 12。攀登者至少需要12以上的体力(大于12)才能安全返回。

输入描述

第一行输入 一个长度为N的数组，表示地图。

第二行输入最大体力。

输出描述

输出一个数字，地图中可以攀登到达的山峰数量

示例

输入

0,1,4,3,1,0,0,1,2,3,1,2,1,0
11

输出

2

解题思路

和【模拟】2023C-攀登者1的区别在于，本题除了需要查看峰值的位置，还需要查看这个峰值是否能够在平地位置攀登过去。

本题需要严格地区分上/下山和上/下坡的区别。在后面的题解中：

  • 上/下山表示从平地到达某个山峰或反之
  • 上/下坡表示从低海拔位置走到高海拔位置或反之

原路返回和非原路返回

攀登山峰的方式，一共可以分为四种情况

  • 从左边上山，往左边下山
  • 从右边上山，往右边下山
  • 从左边上山，往右边下山
  • 从右边上山，从左边下山

其中前两者可以统称为原路返回的攀登方式，后两者可以统称为非原路返回的攀登方式。

在本题中，只需要考虑原路返回的攀登方式，无需考虑非原路返回的攀登方式。

因为两条原路返回路径所花费的体力，一定有一条是小于另外两条非原路返回的攀登方式。

（贪心思想不要尝试在考试的时候证明正确性，相信数学直觉）

原路返回走过的总路程

考虑原路返回的攀登方式，这种登山方式，上坡和下坡走过的总路程是一样多的。也是最方便我们计算的。

以题目所给例子为例，如果我们想从索引7的空地位置向右攀登来到索引12的高度为2的山峰并且原路返回到原来的空地，来回的路线分别用红色和绿色标记出来，会发现上山和下山所走过的总路程其实是一样多的。这个结论对于任何一个山峰、任何一个方向都成立。

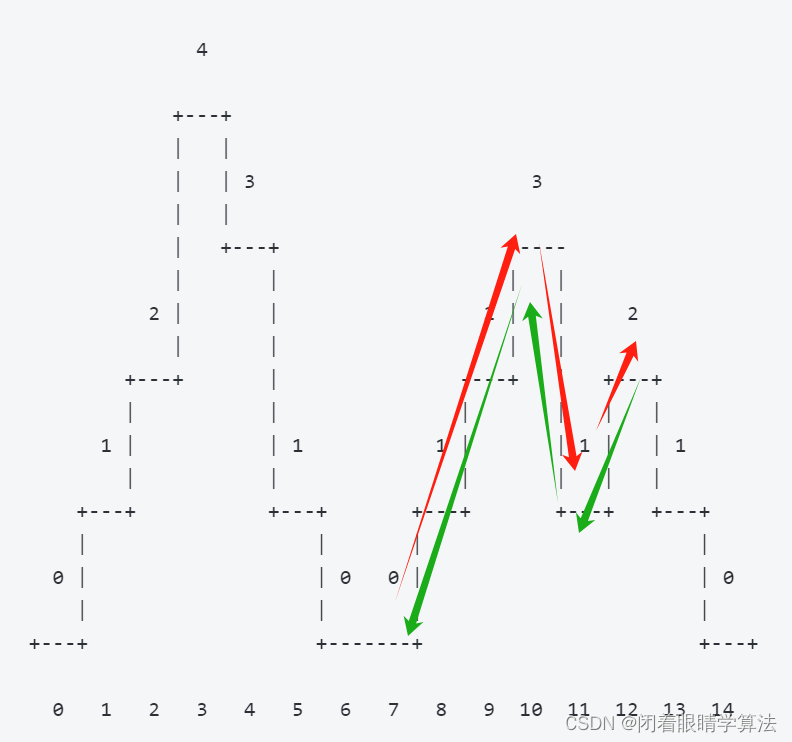
在这里插入图片描述

因此，这里花费的总体力为相邻元素高度差的绝对值的总和乘以3。

其中，相邻元素高度差的绝对值的总和表示走过的总路程，而之所以系数为3是因为上坡和下坡各自要花费2倍和1倍高度差的体力。

所以，对于每一个山峰，我们都可以很容易地计算出从左边的某处空地出发，向右攀登到达这个山峰并且沿原路返回到达空地所需要花费的体力。

如果这个这个体力超过了所给的初始体力，无法到达该山峰。

从左边空地出发原路返回

那么应该如何计算从从左边某处空地出发向右攀登（后面原路返回），能够攀登到的山峰数量？

寻找空地

我们需要找到若干空地作为出发点，这个空地但必须是上山前的最后一个空地。如

[0, 1, 2, 4, 3, 1, 0, 0, 1, 2, 3, 1, 2, 1, 0]⬆                    ⬆

可以通过以下代码实现

space_list = list()
for i in range(n-1):if nums[i] == 0 and nums[i+1] > 0:space_list.append(i)

向右登山

已知最大体力值为power_max，设在攀登过程中所累积的高度差为route_num，对应花费的体力为route_num * 3。

从某一个空地start出发，在一个while循环中不断向右移动，同时更新所经历的高度差route_num。若

  • route_num * 3 > power_max，说明会在攀登过程中体力降为0，无法到达i位置，退出循环
  • 找到了一个山峰，则将位置i记录在数组ans中
    • 注意山峰需要区分边界i == n-1和非边界情况i != n-1
for start in space_list:i = start + 1route_num = 0while i < n and nums[i] != 0:route_num += abs(nums[i] - nums[i-1])if route_num * 3 > power_max:breakif i == n-1 and nums[i] > nums[i-1]:ans.append(i)elif nums[i] > nums[i-1] and nums[i] > nums[i+1]:ans.append(i)i += 1

构建函数

上述两部分合并在一起，可以构建出函数cal_peak_from_left(nums, power_max,, n)，具体实现如下

def cal_peak_from_left(nums, power_max, n):ans = list()space_list = list()for i in range(n-1):if nums[i] == 0 and nums[i+1] > 0:space_list.append(i)for start in space_list:i = start + 1route_num = 0while i < n and nums[i] != 0:route_num += abs(nums[i] - nums[i-1])if route_num * 3 > power_max:breakif i == n-1 and nums[i] > nums[i-1]:ans.append(i)elif nums[i] > nums[i-1] and nums[i] > nums[i+1]:ans.append(i)i += 1return ans

其中返回的列表ans，为从左边空地出发并原路返回，能够攀登到的所有山峰的索引。可以做如下调用

ans_from_left = cal_peak_from_left(heights, power_max, n)

从右边空地出发原路返回

对于是从右边的某处空地出发，向左攀登到某个山峰并沿原路返回到达空地的情况，也存在上述类似的结论。

很容易想到，整个过程是类似的，只不过整个方向反过来了。

一种方法是，可以构建出一个完全类似的函数cal_peak_from_right(nums, power_max, n)

但一种更加简便、代码复用性更强的做法是，我们可以将从右边空地出发向左攀登，看作是对原高度数组进行反转之后，即对heights[::-1]进行从左边空地出发向右攀登得到的结果。即做如下调用

ans_from_right = cal_peak_from_left(heights[::-1], power_max, n)

由于使用了反转，得到计算得到的索引也是反转的，需要进一步处理才能得到原heights数组中的索引，即

ans_from_right = [n-i-1 for i in ans_from_right]

最终取ans_from_left和ans_from_right的交集的长度，即为所有能够攀登到的山峰（不管从左出发还是从右出发原路返回）的索引了。再取并集的长度即为答案。

ans = len(set(ans_from_left + ans_from_right))

*为什么一定是原路返回（严谨证明）

可能有同学就会提出疑问，为什么只考虑原路返回的情况。

这其实是涉及到了贪心思想。

贪心不问出处，问就是数学直觉。

假设到达某个山峰，从左边上山、从右边上山、从左边下山、从右边下山各自花费的体力为A, B, C, D

四种方式所对应的体力值分别为

左上左下 = A + C
左上右下 = A + D
右上右下 = B + D
右上左下 = B + C

每段花费的体力都可以分割为两部分，一部分是上坡、一部分是下坡，分别用下标1和2来表示。那么存在以下的若干式子成立

A = A1 + A2
B = B1 + B2
C = C1 + C2
D = D1 + D2

其中A2, B2, C2, D2不仅表示下坡花费的体力，也同时表示高度

  • A2表示从左边上山经历的下坡高度
  • B2表示从右边上山经历的下坡高度
  • C2表示往左边下山经历的下坡高度
  • D2表示往右边下山经历的下坡高度

由于最终的山峰高度一致，因此存在以下式子成立

C2 - A2 = D2 - B2 > 0

即

C2 + B2 = A2 + D2

如下图所示

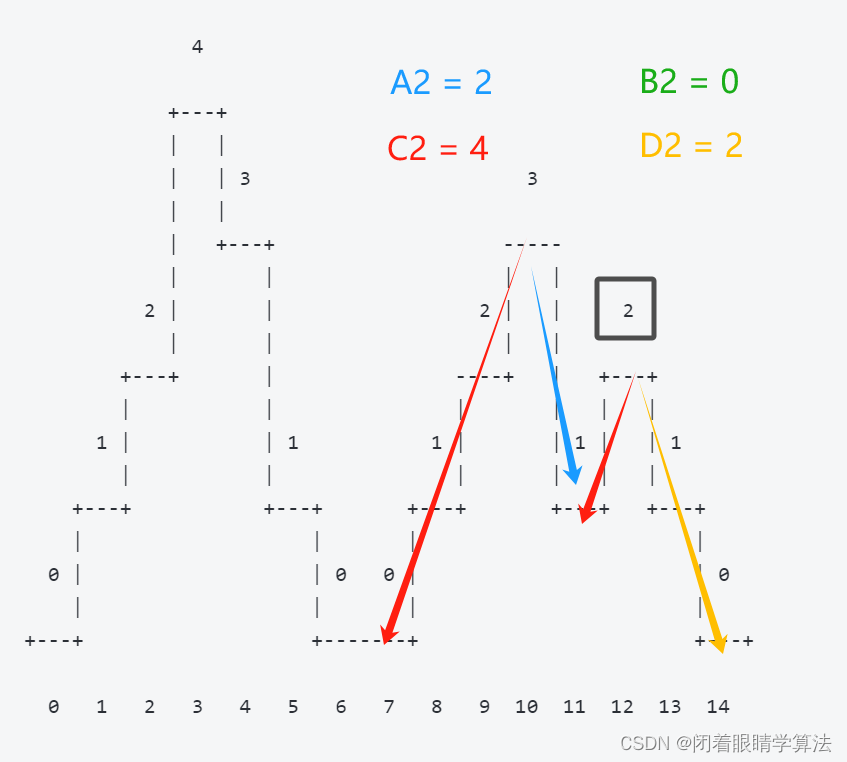
在这里插入图片描述

另外，上坡和下坡的体力消耗也存在倍数关系。譬如，从左边上山的上坡体力消耗A1，是往左边下山的下坡体力消耗C2的两倍。因此存在以下关系

A1 = 2 * C2
C1 = 2 * A2
B1 = 2 * D2
D1 = 2 * B2

代入上述式子可以得到

A = 2 * C2 + A2
B = 2 * D2 + B2
C = 2 * A2 + C2
D = 2 * B2 + D2

进一步可以得到

左上左下 = A + C = (2 * C2 + A2) + (2 * A2 + C2) = 3 * (A2 + C2)
左上右下 = A + D = (2 * C2 + A2) + (2 * B2 + D2) = 2 * (B2 + C2) + (A2 + D2)
右上右下 = B + D = (2 * D2 + B2) + (2 * B2 + D2) = 3 * (B2 + D2)
右上左下 = B + C = (2 * D2 + B2) + (2 * A2 + C2) = 2 * (A2 + D2) + (B2 + C2)

将以下式子带入

C2 + B2 = A2 + D2

可以得到

左上左下 = A + C = (2 * C2 + A2) + (2 * A2 + C2) = 3 * (A2 + C2)
左上右下 = A + D = (2 * C2 + A2) + (2 * B2 + D2) = 3 * (B2 + C2)
右上右下 = B + D = (2 * D2 + B2) + (2 * B2 + D2) = 3 * (B2 + D2)
右上左下 = B + C = (2 * D2 + B2) + (2 * A2 + C2) = 3 * (A2 + D2)

上述方程是非常对称的。又因为

C2 - A2 = D2 - B2 > 0

不妨设C2 >= D2 > A2 >= B2成立（设D2 >= C2 > B2 >= A2也是一样的，会得到(A2 + C2)是最小值）

很容易看出，以下四组数中

(A2 + C2)
(B2 + C2)
(B2 + D2)
(A2 + D2)

一定存在(B2 + D2)是最小值，这里对应着右上右下原路返回的情况。

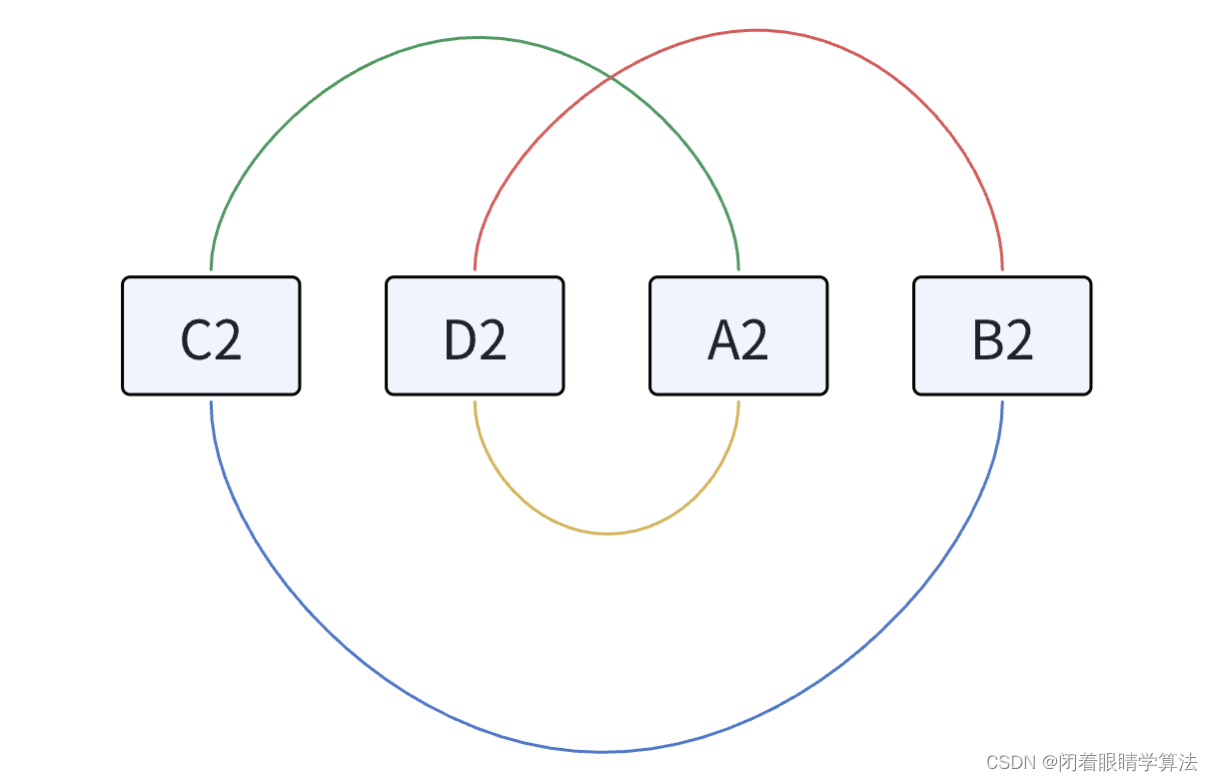
在这里插入图片描述

我们只需要考虑到达山峰的最小情况即可。

代码

python

# 题目：【模拟】2023C-攀登者2
# 分值：200
# 作者：许老师-闭着眼睛学数理化
# 算法：模拟/贪心
# 代码看不懂的地方，请直接在群上提问# 计算从左边空地出发，能够攀登并按照原路返回的山峰数量
def cal_peak_from_left(nums, power_max, n):ans = list()# 记录出发空地的坐标space_list = list()# 考虑所有位置，记录出发的起始位置空地for i in range(n-1):# 如果i为空地，且下一个位置i+1不为空地，则记录位置i，作为一个出发的空地# (即如果出现连续的空地，只需要储存最右边最靠近山体的空地作为出发的起始位置即可)if nums[i] == 0 and nums[i+1] > 0:space_list.append(i)# 考虑每一个起始位置for start in space_list:# 设置初始的i为空地start的下一个位置i = start + 1route_num = 0# 从start+1出发，向右登山# 且不能跨过所有山脉爬到另一头的另一个空地while i < n and nums[i] != 0:# 总高度差新增nums[i]和nums[i-1]之间的高度差route_num += abs(nums[i] - nums[i-1])# 若当前花费体力大于最大体力值，则无法攀登到最新的i处，退出循环# 注意：这里是大于等于，不是大于if route_num * 3 >= power_max:break# 若nums[i]是一座山峰，把i存入ans中# 边界情况if i == n-1 and nums[i] > nums[i-1]:ans.append(i)# 非边界情况elif nums[i] > nums[i-1] and nums[i] > nums[i+1]:ans.append(i)# i递增i += 1# 返回所有能够到达的山峰的索引return ans# 输入高度数组
heights = list(map(int, input().split(",")))
# 获得数组长度
n = len(heights)
# 输入最大体力
power_max = int(input())
# 计算从左边空地出发，向右攀爬，并原路返回能到达的山峰
ans_from_left = cal_peak_from_left(heights, power_max, n)
# 计算从右边空地出发，向左攀爬，并原路返回能到达的山峰
ans_from_right = cal_peak_from_left(heights[::-1], power_max, n)
# 由于使用了反转，得到的索引也是反转的，需要进一步处理才能得到原heights数组中的索引
ans_from_right = [n-i-1 for i in ans_from_right]
# 求ans_from_left和ans_from_right的交集的长度（去重），即为答案
ans = len(set(ans_from_left + ans_from_right))
print(ans)

java

import java.util.*;public class Main {// 计算从左边空地出发，能够攀登并按照原路返回的山峰数量public static List<Integer> calPeakFromLeft(List<Integer> nums, int powerMax, int n) {List<Integer> ans = new ArrayList<>();List<Integer> spaceList = new ArrayList<>();// 记录出发空地的坐标for (int i = 0; i < n - 1; i++) {// 如果i为空地，且下一个位置i+1不为空地，则记录位置i，作为一个出发的空地// (即如果出现连续的空地，只需要储存最右边最靠近山体的空地作为出发的起始位置即可)if (nums.get(i) == 0 && nums.get(i + 1) > 0) {spaceList.add(i);}}// 考虑每一个起始位置for (int start : spaceList) {// 设置初始的i为空地start的下一个位置int i = start + 1;int routeNum = 0;// 从start+1出发，向右登山// 且不能跨过所有山脉爬到另一头的另一个空地while (i < n && nums.get(i) != 0) {// 总高度差新增nums[i]和nums[i-1]之间的高度差routeNum += Math.abs(nums.get(i) - nums.get(i - 1));// 若总高度大于等于最大高度差，则无法攀登到最新的i处，退出循环// 注意：这里是大于等于，不是大于if (routeNum * 3 >= powerMax) {break;}// 若nums[i]是一座山峰，把i存入ans中// 边界情况if (i == n - 1 && nums.get(i) > nums.get(i - 1)) {ans.add(i);}// 非边界情况else if (nums.get(i) > nums.get(i - 1) && nums.get(i) > nums.get(i + 1)) {ans.add(i);}// i递增i++;}}// 返回所有能够到达的山峰的索引return ans;}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);String input = scanner.nextLine();List<Integer> heights = new ArrayList<>();String[] heightStrings = input.split(",");for (String heightString : heightStrings) {heights.add(Integer.parseInt(heightString));}int n = heights.size();int powerMax = scanner.nextInt();// 计算从左边空地出发，向右攀爬，并原路返回能到达的山峰List<Integer> ansFromLeft = calPeakFromLeft(heights, powerMax, n);// 计算从右边空地出发，向左攀爬，并原路返回能到达的山峰List<Integer> reversedHeights = new ArrayList<>(heights);Collections.reverse(reversedHeights);List<Integer> ansFromRight = calPeakFromLeft(reversedHeights, powerMax, n);// 由于使用了反转，得到的索引也是反转的，需要进一步处理才能得到原heights数组中的索引for (int i = 0; i < ansFromRight.size(); i++) {ansFromRight.set(i, n - ansFromRight.get(i) - 1);}// 使用 HashSet 来存储并集的结果，去重Set<Integer> ansSet = new HashSet<>(ansFromLeft);ansSet.addAll(ansFromRight);// 输出结果System.out.println(ansSet.size());}
}

cpp

#include <iostream>
#include <vector>
#include <cmath>
#include <unordered_set>
#include <sstream>using namespace std;// 计算从左边空地出发，能够攀登并按照原路返回的山峰数量
vector<int> cal_peak_from_left(vector<int>& nums, int power_max, int n) {vector<int> ans;vector<int> space_list;// 记录出发空地的坐标for (int i = 0; i < n - 1; i++) {// 如果i为空地，且下一个位置i+1不为空地，则记录位置i，作为一个出发的空地// (即如果出现连续的空地，只需要储存最右边最靠近山体的空地作为出发的起始位置即可)if (nums[i] == 0 && nums[i+1] > 0) {space_list.push_back(i);}}// 考虑每一个起始位置for (int start : space_list) {// 设置初始的i为空地start的下一个位置int i = start + 1;int route_num = 0;// 从start+1出发，向右登山// 且不能跨过所有山脉爬到另一头的另一个空地while (i < n && nums[i] != 0) {// 总高度差新增nums[i]和nums[i-1]之间的高度差route_num += abs(nums[i] - nums[i - 1]);// 若总高度大于等于最大高度差，则无法攀登到最新的i处，退出循环// 注意：这里是大于等于，不是大于if (route_num * 3 >= power_max) {break;}// 若nums[i]是一座山峰，把i存入ans中// 边界情况if (i == n - 1 && nums[i] > nums[i - 1]) {ans.push_back(i);}// 非边界情况else if (nums[i] > nums[i - 1] && nums[i] > nums[i + 1]) {ans.push_back(i);}// i递增i++;}}// 返回所有能够到达的山峰的索引return ans;
}int main() {string input;getline(cin, input);vector<int> heights;int num, power_max;// 使用 stringstream 解析输入高度数组stringstream ss(input);string temp;while (getline(ss, temp, ',')) {num = stoi(temp);heights.push_back(num);}// 获得数组长度int n = heights.size();// 输入最大体力cin >> power_max;// 计算从左边空地出发，向右攀爬，并原路返回能到达的山峰vector<int> ans_from_left = cal_peak_from_left(heights, power_max, n);// 计算从右边空地出发，向左攀爬，并原路返回能到达的山峰vector<int> reversed_heights(heights.rbegin(), heights.rend());vector<int> ans_from_right = cal_peak_from_left(reversed_heights, power_max, n);// 由于使用了反转，得到的索引也是反转的，需要进一步处理才能得到原heights数组中的索引for (int i = 0; i < ans_from_right.size(); i++) {ans_from_right[i] = n - ans_from_right[i] - 1;}// 使用 unordered_set 来存储交集的结果，去重unordered_set<int> ans_set;for (int val : ans_from_left) {ans_set.insert(val);}for (int val : ans_from_right) {ans_set.insert(val);}// 输出结果cout << ans_set.size() << endl;return 0;
}

时空复杂度

时间复杂度：O(N)。

空间复杂度：O(N)。

华为OD算法/大厂面试高频题算法练习冲刺训练

  • 华为OD算法/大厂面试高频题算法冲刺训练目前开始常态化报名！目前已服务300+同学成功上岸！

  • 课程讲师为全网50w+粉丝编程博主@吴师兄学算法 以及小红书头部编程博主@闭着眼睛学数理化

  • 每期人数维持在20人内，保证能够最大限度地满足到每一个同学的需求，达到和1v1同样的学习效果！

  • 60+天陪伴式学习，40+直播课时，300+动画图解视频，300+LeetCode经典题，200+华为OD真题/大厂真题，还有简历修改、模拟面试、专属HR对接将为你解锁

  • 可上全网独家的欧弟OJ系统练习华子OD、大厂真题

  • 可查看链接 大厂真题汇总 & OD真题汇总(持续更新)

  • 绿色聊天软件戳 od1336了解更多

这篇关于【Py/Java/C++三种语言OD2023C卷真题】20天拿下华为OD笔试之【模拟】2023C-攀登者2【欧弟算法】全网注释最详细分类最全的华为OD真题题解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/828136。

相关文章

JVM 的类初始化机制

JVM 的类初始化机制

前言 当你在 Java 程序中new对象时，有没有考虑过 JVM 是如何把静态的字节码（byte code）转化为运行时对象的呢，这个问题看似简单，但清楚的同学相信也不会太多，这篇文章首先介绍 JVM 类初始化的机制，然后给出几个易出错的实例来分析，帮助大家更好理解这个知识点。 JVM 将字节码转化为运行时对象分为三个阶段，分别是：loading 、Linking、initialization
阅读更多...
Spring Security 基于表达式的权限控制

Spring Security 基于表达式的权限控制

前言 spring security 3.0已经可以使用spring el表达式来控制授权，允许在表达式中使用复杂的布尔逻辑来控制访问的权限。 常见的表达式 Spring Security可用表达式对象的基类是SecurityExpressionRoot。 表达式描述hasRole([role])用户拥有制定的角色时返回true （Spring security默认会带有ROLE_前缀）,去
阅读更多...
浅析Spring Security认证过程

浅析Spring Security认证过程

类图 为了方便理解Spring Security认证流程，特意画了如下的类图，包含相关的核心认证类 概述 核心验证器 AuthenticationManager 该对象提供了认证方法的入口，接收一个Authentiaton对象作为参数; public interface AuthenticationManager {Authentication authenticate(Authenti
阅读更多...
Spring Security--Architecture Overview

Spring Security--Architecture Overview

1 核心组件 这一节主要介绍一些在Spring Security中常见且核心的Java类，它们之间的依赖，构建起了整个框架。想要理解整个架构，最起码得对这些类眼熟。 1.1 SecurityContextHolder SecurityContextHolder用于存储安全上下文（security context）的信息。当前操作的用户是谁，该用户是否已经被认证，他拥有哪些角色权限…这些都被保
阅读更多...
Spring Security基于数据库验证流程详解

Spring Security基于数据库验证流程详解

Spring Security 校验流程图 相关解释说明（认真看哦） AbstractAuthenticationProcessingFilter 抽象类 /*** 调用 #requiresAuthentication(HttpServletRequest, HttpServletResponse) 决定是否需要进行验证操作。* 如果需要验证，则会调用 #attemptAuthentica
阅读更多...
Spring Security 从入门到进阶系列教程

Spring Security 从入门到进阶系列教程

Spring Security 入门系列 《保护 Web 应用的安全》 《Spring-Security-入门（一）：登录与退出》 《Spring-Security-入门（二）：基于数据库验证》 《Spring-Security-入门（三）：密码加密》 《Spring-Security-入门（四）：自定义-Filter》 《Spring-Security-入门（五）：在 Sprin
阅读更多...
Java架构师知识体认识

Java架构师知识体认识

源码分析 常用设计模式 Proxy代理模式Factory工厂模式Singleton单例模式Delegate委派模式Strategy策略模式Prototype原型模式Template模板模式 Spring5 beans 接口实例化代理Bean操作 Context Ioc容器设计原理及高级特性Aop设计原理Factorybean与Beanfactory Transaction 声明式事物
阅读更多...
不懂推荐算法也能设计推荐系统

不懂推荐算法也能设计推荐系统

本文以商业化应用推荐为例，告诉我们不懂推荐算法的产品，也能从产品侧出发， 设计出一款不错的推荐系统。 相信很多新手产品，看到算法二字，多是懵圈的。 什么排序算法、最短路径等都是相对传统的算法（注：传统是指科班出身的产品都会接触过）。但对于推荐算法，多数产品对着网上搜到的资源，都会无从下手。特别当某些推荐算法 和 “AI”扯上关系后，更是加大了理解的难度。 但，不了解推荐算法，就无法做推荐系
阅读更多...
python: 多模块(.py)中全局变量的导入

python: 多模块(.py)中全局变量的导入

文章目录 global关键字可变类型和不可变类型数据的内存地址单模块(单个py文件)的全局变量示例总结 多模块(多个py文件)的全局变量from x import x导入全局变量示例 import x导入全局变量示例 总结 global关键字 global 的作用范围是模块(.py)级别： 当你在一个模块（文件）中使用 global 声明变量时，这个变量只在该模块的全局命名空
阅读更多...
Java进阶13讲__第12讲_1/2

Java进阶13讲__第12讲_1/2

多线程、线程池 1.  线程概念 1.1  什么是线程 1.2  线程的好处 2.   创建线程的三种方式 注意事项 2.1  继承Thread类 2.1.1 认识  2.1.2  编码实现  package cn.hdc.oop10.Thread;import org.slf4j.Logger;import org.slf4j.LoggerFactory
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2