传说时间复杂度为0(n)的排序

   前面已经介绍了几种排序算法，像插入排序（直接插入排序，折半插入排序，希尔排序）、交换排序（冒泡排序，快速排序）、选择排序（简单选择排序，堆排序）、2-路归并排序（见我的另一篇文章：各种内部排序算法的实现）等，这些排序算法都有一个共同的特点，就是基于比较。本文将介绍三种非比较的排序算法：计数排序，基数排序，桶排序。它们将突破比较排序的Ω(nlgn)下界，以线性时间运行。

一、比较排序算法的时间下界

所谓的比较排序是指通过比较来决定元素间的相对次序。

“定理：对于含n个元素的一个输入序列，任何比较排序算法在最坏情况下，都需要做Ω(nlgn)次比较。”

也就是说，比较排序算法的运行速度不会快于nlgn，这就是基于比较的排序算法的时间下界。

通过决策树（Decision-Tree）可以证明这个定理，关于决策树的定义以及证明过程在这里就不赘述了。你可以自己去查找资料，推荐观看《MIT公开课：线性时间排序》。

根据上面的定理，我们知道任何比较排序算法的运行时间不会快于nlgn。那么我们是否可以突破这个限制呢？当然可以，接下来我们将介绍三种线性时间的排序算法，它们都不是通过比较来排序的，因此，下界Ω(nlgn)对它们不适用。

二、计数排序（Counting Sort）

计数排序的基本思想就是对每一个输入元素x，确定小于x的元素的个数，这样就可以把x直接放在它在最终输出数组的位置上，例如：

算法的步骤大致如下：

• 找出待排序的数组中最大和最小的元素

• 统计数组中每个值为i的元素出现的次数，存入数组C的第i项

• 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）

• 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

C++代码：

 /*************************************************************************
     > File Name: CountingSort.cpp
     > Author: SongLee
     > E-mail: lisong.shine@qq.com
     > Created Time: 2014年06月11日 星期三 00时08分55秒
     > Personal Blog: http://songlee24.github.io
  ************************************************************************/
 #include<iostream>
 using namespace std;

 /*
  *计数排序：A和B为待排和目标数组，k为数组中最大值,len为数组长度
  */
 void CountingSort(int A[], int B[], int k, int len)
 {
     int C[k+1];
     for(int i=0; i<k+1; ++i)
         C[i] = 0;
     for(int i=0; i<len; ++i)
         C[A[i]] += 1;
     for(int i=1; i<k+1; ++i)
         C[i] = C[i] + C[i-1];
     for(int i=len-1; i>=0; --i)
     {
         B[C[A[i]]-1] = A[i];
         C[A[i]] -= 1;
     }
 }

 /* 输出数组 */
 void print(int arr[], int len)
 {
     for(int i=0; i<len; ++i)
         cout << arr[i] << " ";
     cout << endl;
 }

 /* 测试 */
 int main()
 {
     int origin[8] = {4,5,3,0,2,1,15,6};
     int result[8];
     print(origin, 8);
     CountingSort(origin, result, 15, 8);
     print(result, 8);
     return 0;
 }

当输入的元素是0到k之间的整数时，时间复杂度是O(n+k)，空间复杂度也是O(n+k)。当k不是很大并且序列比较集中时，计数排序是一个很有效的排序算法。计数排序是一个稳定的排序算法。

可能你会发现，计数排序似乎饶了点弯子，比如当我们刚刚统计出C，C[i]可以表示A中值为i的元素的个数，此时我们直接顺序地扫描C，就可以求出排序后的结果。的确是这样，不过这种方法不再是计数排序，而是桶排序，确切地说，是桶排序的一种特殊情况。

三、桶排序（Bucket Sort）

桶排序（Bucket Sort）的思想是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法）。当要被排序的数组内的数值是均匀分配的时候，桶排序可以以线性时间运行。桶排序过程动画演示：Bucket Sort，桶排序原理图如下：

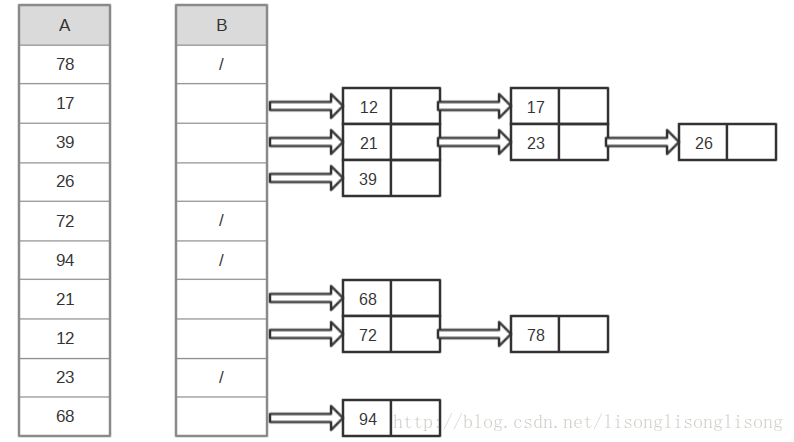
C++代码：

 /*************************************************************************
     > File Name: BucketSort.cpp
     > Author: SongLee
     > E-mail: lisong.shine@qq.com
     > Created Time: 2014年06月11日 星期三 09时17分32秒
     > Personal Blog: http://songlee24.github.io
  ************************************************************************/
 #include<iostream>
 using namespace std;

 /* 节点 */
 struct node
 {
     int value;
     node* next;
 };

 /* 桶排序 */
 void BucketSort(int A[], int max, int len)
 {
     node bucket[len];
     int count=0;
     for(int i=0; i<len; ++i)
     {
         bucket[i].value = 0;
         bucket[i].next = NULL;
     }

     for(int i=0; i<len; ++i)
     {
         node *ist = new node();
         ist->value = A[i];
         ist->next = NULL;
         int idx = A[i]*len/(max+1); // 计算索引
         if(bucket[idx].next == NULL)
         {
             bucket[idx].next = ist;
         }
         else /* 按大小顺序插入链表相应位置 */
         {
             node *p = &bucket[idx];
             node *q = p->next;
             while(q!=NULL && q->value <= A[i])
             {
                 p = q;
                 q = p->next;
             }
             ist->next = q;
             p->next = ist;
         }
     }

     for(int i=0; i<len; ++i)
     {
         node *p = bucket[i].next;
         if(p == NULL)
             continue;
         while(p!= NULL)
         {
             A[count++] = p->value;
             p = p->next;
         }
     }
 }

 /* 输出数组 */
 void print(int A[], int len)
 {
     for(int i=0; i<len; ++i)
         cout << A[i] << " ";
     cout << endl;
 }

 /* 测试 */
 int main()
 {
     int row[11] = {24,37,44,12,89,93,77,61,58,3,100};
     print(row, 11);
     BucketSort(row, 235, 11);
     print(row, 11);
     return 0;
 }

四、基数排序（Radix Sort）

基数排序（Radix Sort）是一种非比较型排序算法，它将整数按位数切割成不同的数字，然后按每个位分别进行排序。基数排序的方式可以采用MSD（Most significant digital）或LSD（Least significant digital），MSD是从最高有效位开始排序，而LSD是从最低有效位开始排序。

当然我们可以采用MSD方式排序，按最高有效位进行排序，将最高有效位相同的放到一堆，然后再按下一个有效位对每个堆中的数递归地排序，最后再将结果合并起来。但是，这样会产生很多中间堆。所以，通常基数排序采用的是LSD方式。

LSD基数排序实现的基本思路是将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。需要注意的是，对每一个数位进行排序的算法必须是稳定的，否则就会取消前一次排序的结果。通常我们使用计数排序或者桶排序作为基数排序的辅助算法。基数排序过程动画演示：Radix Sort

C++实现（使用计数排序）：

 /*************************************************************************
     > File Name: RadixSort.cpp
     > Author: SongLee
     > E-mail: lisong.shine@qq.com
     > Created Time: 2014年06月22日 星期日 12时04分37秒
     > Personal Blog: http://songlee24.github.io
  ************************************************************************/
 #include<iostream>
 using namespace std;

 // 找出整数num第n位的数字
 int findIt(int num, int n)
 {
     int power = 1;
     for (int i = 0; i < n; i++)
     {
         power *= 10;
     }
     return (num % power) * 10 / power;
 }

 // 基数排序（使用计数排序作为辅助）
 void RadixSort(int A[], int len, int k)
 {
     for(int i=1; i<=k; ++i)
     {
         int C[10] = {0};   // 计数数组
         int B[len];        // 结果数组

         for(int j=0; j<len; ++j)
         {
             int d = findIt(A[j], i);
             C[d] += 1;
         }

         for(int j=1; j<10; ++j)
             C[j] = C[j] + C[j-1];

         for(int j=len-1; j>=0; --j)
         {
             int d = findIt(A[j], i);
             C[d] -= 1;
             B[C[d]] = A[j];
         }

         // 将B中排好序的拷贝到A中
         for(int j=0; j<len; ++j)
             A[j] = B[j];
     }
 }

 // 输出数组
 void print(int A[], int len)
 {
     for(int i=0; i<len; ++i)
         cout << A[i] << " ";
     cout << endl;
 }

 // 测试
 int main()
 {
     int A[8] = {332, 653, 632, 5, 755, 433, 722, 48};
     print(A, 8);
     RadixSort(A, 8, 3);
     print(A, 8);
     return 0;
 }

基数排序的时间复杂度是 O(k·n)，其中n是排序元素个数，k是数字位数。注意这不是说这个时间复杂度一定优于O(nlgn)，因为n可能具有比较大的系数k。

另外，基数排序不仅可以对整数排序，也可以对有多个关键字域的记录进行排序。例如，根据三个关键字年、月、日来对日期进行排序。