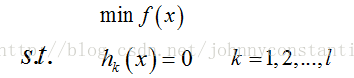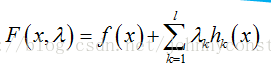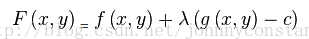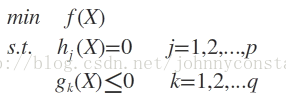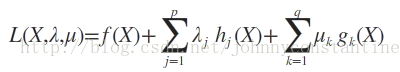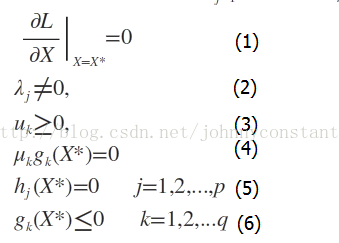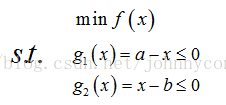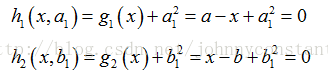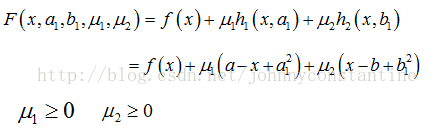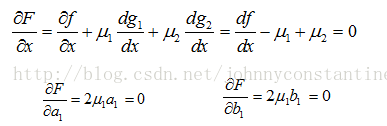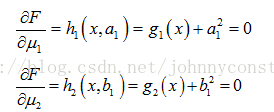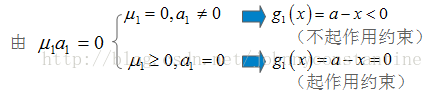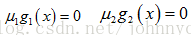本文主要是介绍SVM中KKT条件介绍,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
KKT条件介绍
最近学习的时候用到了最优化理论,但是我没有多少这方面的理论基础。于是翻了很多大神的博客把容易理解的内容记载到这篇博客中。因此这是篇汇总博客,不算是全部原创,但是基础理论,应该也都差不多吧。因才疏学浅,有纰漏的地方恳请指出。
KKT条件是解决最优化问题的时用到的一种方法。我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值。提到KKT条件一般会附带的提一下拉格朗日乘子。对学过高等数学的人来说比较拉格朗日乘子应该会有些印象。二者均是求解最优化问题的方法,不同之处在于应用的情形不同。
一般情况下,最优化问题会碰到一下三种情况:
(1)无约束条件
这是最简单的情况,解决方法通常是函数对变量求导,令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。
(2)等式约束条件
设目标函数为f(x),约束条件为hk(x),形如
s.t. 表示subject to ,“受限于”的意思,l表示有l个约束条件。
则解决方法是消元法或者拉格朗日法。消元法比较简单不在赘述,拉格朗日法这里在提一下,因为后面提到的KKT条件是对拉格朗日乘子法的一种泛化。
定义拉格朗日函数F(x),
其中λk是各个约束条件的待定系数。
然后解变量的偏导方程:
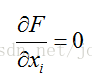
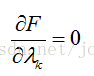
如果有l个约束条件,就应该有l+1个方程。求出的方程组的解就可能是最优化值(高等数学中提到的极值),将结果带回原方程验证就可得到解。
至于为什么这么做可以求解最优化?维基百科上给出了一个比较好的直观解释。
举个二维最优化的例子:
min f(x,y)
s.t. g(x,y) = c
这里画出z=f(x,y)的等高线(函数的等高线定义:二元函数z = f(x,y)在空间表示的是一张曲面,这个曲面与平面z = c的交线在xoy面上的投影曲线f(x,y)=c称为函数z=f(x,y)的一条登高线。):

绿线标出的是约束 g(x,y)=c 的点的轨迹。蓝线是 f(x,y) 的等高线。箭头表示斜率,和等高线的法线平行。从梯度的方向上来看,显然有d1>d2。绿色的线是约束,也就是说,只要正好落在这条绿线上的点才可能是满足要求的点。如果没有这条约束,f(x,y)的最小值应该会落在最小那圈等高线内部的某一点上。而现在加上了约束,最小值点应该在哪里呢?显然应该是在f(x,y)的等高线正好和约束线相切的位置,因为如果只是相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小,只有到等高线与目标函数的曲线相切的时候,可能取得最优值。
如果我们对约束也求梯度∇g(x,y),则其梯度如图中绿色箭头所示。很容易看出来,要想让目标函数f(x,y)的等高线和约束相切,则他们切点的梯度一定在一条直线上。
即:∇f(x,y)=λ(∇g(x,y)-C)
其中λ可以是任何非0实数。
一旦求出λ的值,将其套入下式,易求在无约束极值和极值所对应的点。
这就是拉格朗日函数的由来。
(3)不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下:
则我们定义不等式约束下的拉格朗日函数L,则L表达式为:
其中f(x)是原目标函数,hj(x)是第j个等式约束条件,λj是对应的约束系数,gk是不等式约束,uk是对应的约束系数。0
此时若要求解上述优化问题,必须满足下述条件(也是我们的求解条件):
这些求解条件就是KKT条件。(1)是对拉格朗日函数取极值时候带来的一个必要条件,(2)是拉格朗日系数约束(同等式情况),(3)是不等式约束情况,(4)是互补松弛条件,(5)、(6)是原约束条件。
对于一般的任意问题而言,KKT条件是使一组解成为最优解的必要条件,当原问题是凸问题的时候,KKT条件也是充分条件。
关于条件(3),后面一篇博客中给出的解释是:我们构造L(x,λ,u)函数,是希望L(x,λ,u)<=f(x)的(min表示求最小值)。在L(x,λ,u)表达式中第二项为0,若使得第三项小于等于0就必须使得系数u>=0,这也就是条件(3)。
关于条件(4),直观的解释可以这么看:要求得L(x,λ,u)的最小值一定是三个公式项中取得最小值,此时第三项最小就是等于0值的时候。稍微正式一点的解释,是由松弛变量推导而来。
为方便表示,举个简单的例子:
现有如下不等式约束优化问题:
此时引入松弛变量可以将不等式约束变成等式约束。设a1和b1为两个松弛变量,则上述的不等式约束可写为:
则该问题的拉格朗日函数为:
根据拉格朗日乘子法,求解方程组:
则
同样 u2b1=0,来分析g2(x)起作用和不起作用约束。
于是推出条件:
KKT条件介绍完毕。
参考文献:
[1]kkt条件:点击打开链接
[2]kkt条件:点击打开链接
[3]拉格朗日乘子法:点击打开链接
[4]对偶理论:点击打开链接
这篇关于SVM中KKT条件介绍的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!