本文主要是介绍王道机试C++第8章递归与分治 Day35和蓝桥杯两道真题程序,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
第 8 章 递归与分治
8.1 递归策略
例:n 的阶乘
题目描述:

代码表示:
#include <bits/stdc++.h>
using namespace std;int Factorial(int n){if(n==1){return 1;}else{return Factorial(n-1)*n;}
}
int main() {int n;scanf("%d",&n);printf("%d\n", Factorial(n));return 0;
}
例:汉诺塔 III
题目描述:
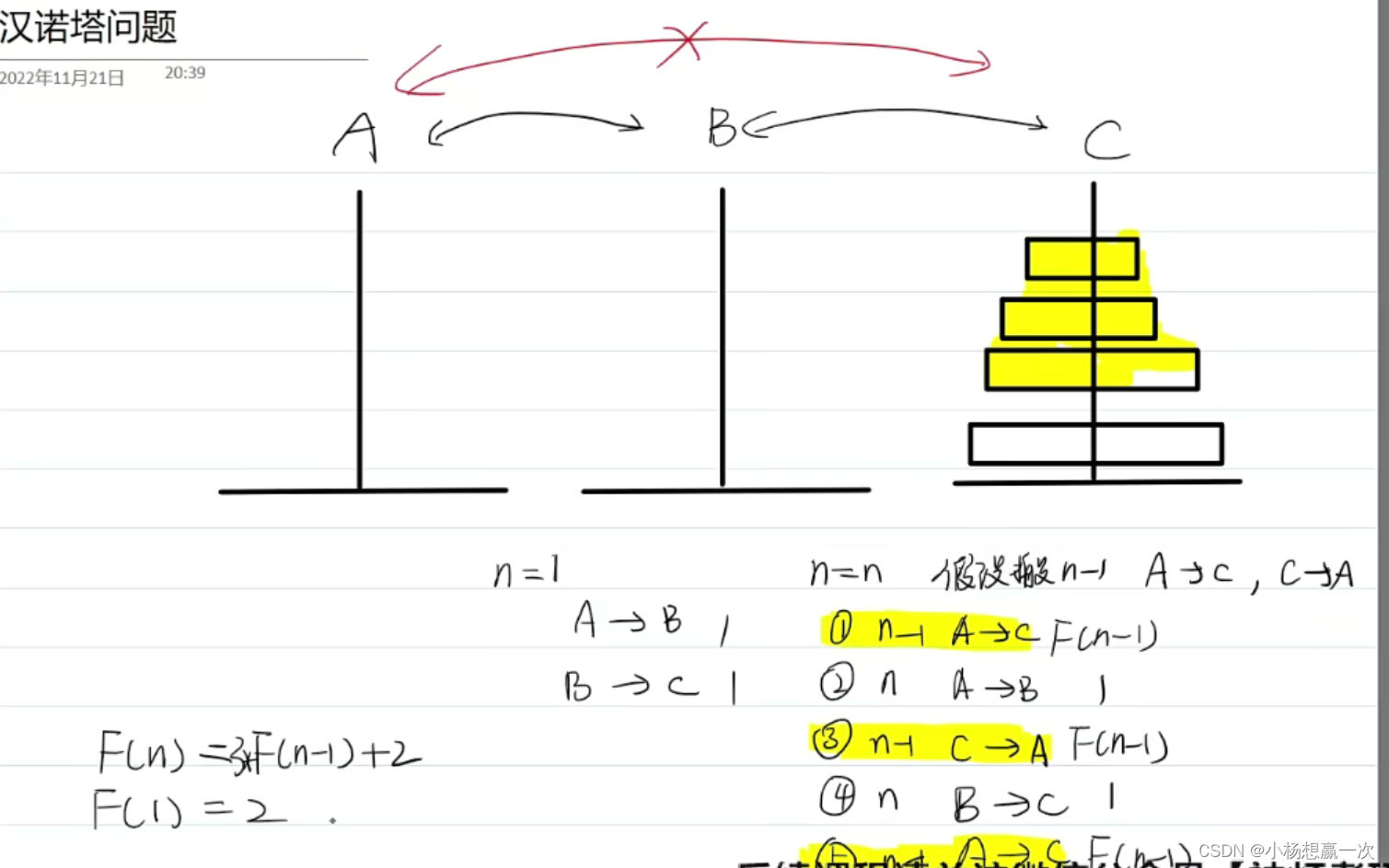
代码表示:
#include <bits/stdc++.h>
using namespace std;
long long hanoi(int n){if(n==1){return 2;}else{return 3*hanoi(n-1)+2;}
}
int main() {int n;while (scanf("%d",&n)!=EOF){printf("%lld",hanoi(n));}return 0;
}
思路提示:
若从第一根杆上移动 N 个圆盘到第三根杆上需要 F[N] 次移动,那么综上所述 F[N] 的组成方式 如下:先移动 N -1个圆盘到第三根杆上需要 F[N -1] 次移动,然后将最大的圆盘移动到中间杆上需要 1 次移动,再将 N -1个圆盘移动回第一根杆上同样需要 F[N-1] 次移动,移动最大的盘子到第三根杆上需要 1 次移动,最后将 N -1个圆盘移动到第三根杆上需要 F[N -1] 次移动,于是便有了 F[N] = 3F[N -1] + 2 。也就是说,从第一根杆上移动 N 个圆盘到第三根杆上,需要三次从第一根杆上移动 N -1个圆盘到第三根杆上,外加两次对最大圆盘的移动。这样就可以将移动 N 个圆盘的问题转换为问题相同但规模更小的移动 N -1个圆盘的问题。
递归出口:当 N 为 1 时,即从第一根杆上移动一个盘子到第三根杆上,所需的移动次数显而易见为 2。移动一个盘子所需次数是最底层的子问题,该子问题不可继续分解且易于求解。这便是递归的出口。
8.2 分治法
例:Fibonacci(上交大复试)
题目描述
斐波那契数列{0,1,1,2,3,5,8,13,21,34,55...}由递归定义: F0=0 F1=1 Fn=Fn-1+Fn-2,n>=2 编写一个程序来计算斐波那契数列。
输入描述:每个情况都包含一个数字 n,您应该计算 Fn.(0<=n<=30) 。
输出描述:对于每种情况,在单独的行上打印一个数字 Fn,这意味着第 n 个斐波那契数列.
输入:1
代码表示
#include <bits/stdc++.h>
using namespace std;
int feibo(int n){if(n==0){return 0;}else if(n==1){return 1;}else{return feibo(n-1)+feibo(n-2);}
}
int main() {int n;while (scanf("%d",&n)!=EOF){printf("%d",feibo(n));}return 0;
}
例:二叉树(北大上机)
题目描述:
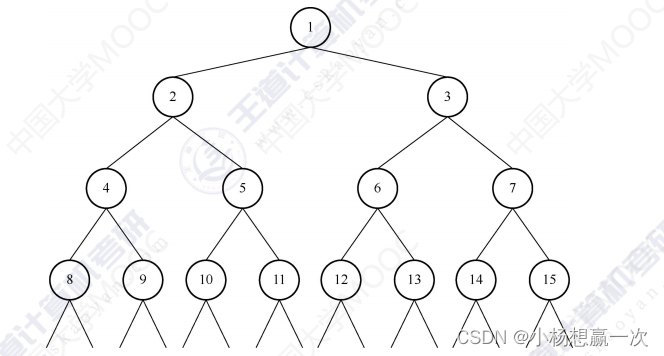
代码表示:
#include <bits/stdc++.h>
using namespace std;
int tree(int m,int n){if(m>n){return 0;//边界情况 }else{return 1+tree(2*m,n)+tree(2*m+1,n);}
}
int main() {int m,n;while (scanf("%d%d",&m,&n)!=EOF){if(m==0){break;}printf("%d",tree(m,n));}return 0;
}[蓝桥杯 2015 省 B] 移动距离
题目描述
X 星球居民小区的楼房全是一样的,并且按矩阵样式排列。其楼房的编号为1,2,3,⋯ 。当排满一行时,从下一行相邻的楼往反方向排号。
比如:当小区排号宽度为 6 时,开始情形如下:
1 2 3 4 5 6
12 11 10 9 8 7
13 14 15 .....
我们的问题是:已知了两个楼号 m 和 n,需要求出它们之间的最短移动距离。(不能斜线方向移动)
输入格式
输入为 3 个整数w,m,n,空格分开,都在 1到 10000 范围内。w 为排号宽度,m,n 为待计算的楼号。
输出格式
要求输出一个整数,表示 m 与 n 两楼间最短移动距离

代码表示
#include <bits/stdc++.h>
using namespace std;
int w,m,n,kx,ky,x=0,y=1;//m坐标x,y;n坐标kx,ky
int main()
{scanf("%d%d%d",&w,&m,&n);if(n>m) swap(n,m);for(register int i=1;i<=m;i++)//枚举从1到m所有数的坐标{if(y%2==1)//正方向{x++;if(x>w) x=w,y++;}else //反方向{x--;if(x<1) x=1,y++;}if(i==n) kx=x,ky=y; //记录n的坐标}printf("%d",abs(kx-x)+abs(ky-y));return 0;
}
心得体会:
这个代码很巧妙,实际上所列出的数实际是什么根本就不重要,重要的是这个点所在坐标位置数的大小。以此来求解两坐标的距离。abs(kx - x)用于计算目标位置和当前位置在水平方向上的距离差的绝对值。
[蓝桥杯 2017 省 B] 日期问题
题目描述
小明正在整理一批历史文献。这些历史文献中出现了很多日期。小明知道这些日期都在 1960 年 1 月 1 日至 2059 年 12 月 31 日。令小明头疼的是,这些日期采用的格式非常不统一,有采用年/月/日的,有采用月/日/年的,还有采用日/月/年的。更加麻烦的是,年份也都省略了前两位,使得文献上的一个日期,存在很多可能的日期与其对应。比如 02/03/04,可能是 2002 年 03 月 04 日、2004 年 02 月 03 日或 2004 年 03 月 02 日。给出一个文献上的日期,你能帮助小明判断有哪些可能的日期对其对应吗?
输入格式
一个日期,格式是 AA/BB/CC。(0≤A,B,C≤9)
输出格式
输出若干个不相同的日期,每个日期一行,格式是 yyyy-MM-dd。多个日期按从早到晚排列。
#include <bits/stdc++.h>
using namespace std;char a[20];//存储输入的日期
int M[20]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int main()
{int l,i,j,k,x,y,z;scanf("%s",a);l=strlen(a);//解析日期中的年份,日期,月份为整数 x=(a[0]-48)*10+a[1]-48;y=(a[3]-48)*10+a[4]-48; z=(a[6]-48)*10+a[7]-48;for(i=1960;i<=2059;i++){if(i%400==0||(i%4==0&&i%100!=0)) //判断闰年M[2]=29;//将二月的天数设为29 for(j=1;j<=12;j++)//遍历每个月 {for(k=1;k<=M[j];k++)//遍历每个月的每一天
//这个i%100也就是遍历到某个四位数的年份取其后两位 if((x==i%100&&y==j&&z==k)||(z==i%100&&x==j&&y==k)||(z==i%100&&y==j&&x==k)){cout<<i<<"-";if(j<10)cout<<0;cout<<j<<"-";if(k<10)cout<<0;cout<<k<<endl;} }M[2]=28;//别忘了 }
}心得体会:
1、在ASCII编码中,数字字符'0'的ASCII码是48,而其后的字符依次递增。因此,通过将字符'a[0]'减去48,可以得到对应的数字值。在这段代码中,a[0]是输入日期字符串的第一个字符,例如'0'、'1'、'2'等。由于这些字符是ASCII码表中的字符表示形式,而我们需要得到的是其对应的数字值,所以需要将字符'0'的ASCII码值48减去。然后,将结果乘以10,以便处理两位数的年份。接下来,从字符'a[1]'中减去48,再将结果与之前的乘积相加,从而得到两位数的年份值。
2、这道题开始处解析日期的时候就很灵活,后续采用暴力循环,接着写if语句来取不同日期的值。
这篇关于王道机试C++第8章递归与分治 Day35和蓝桥杯两道真题程序的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




