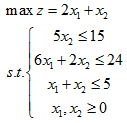本文主要是介绍运筹说 第20期 | 算法介绍之单纯形法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

我们以16期的例题为例,选取Matlab以及Excel这两个软件对如何实现一般的单纯形法、大M法和两阶段法进行讲解,题目如下:
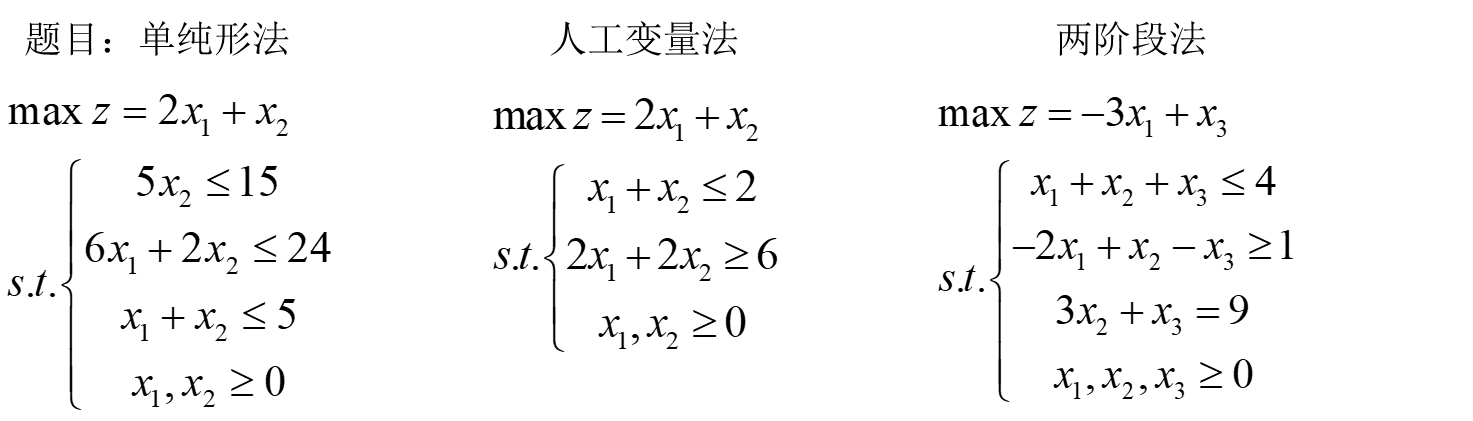
一、Matlab求解
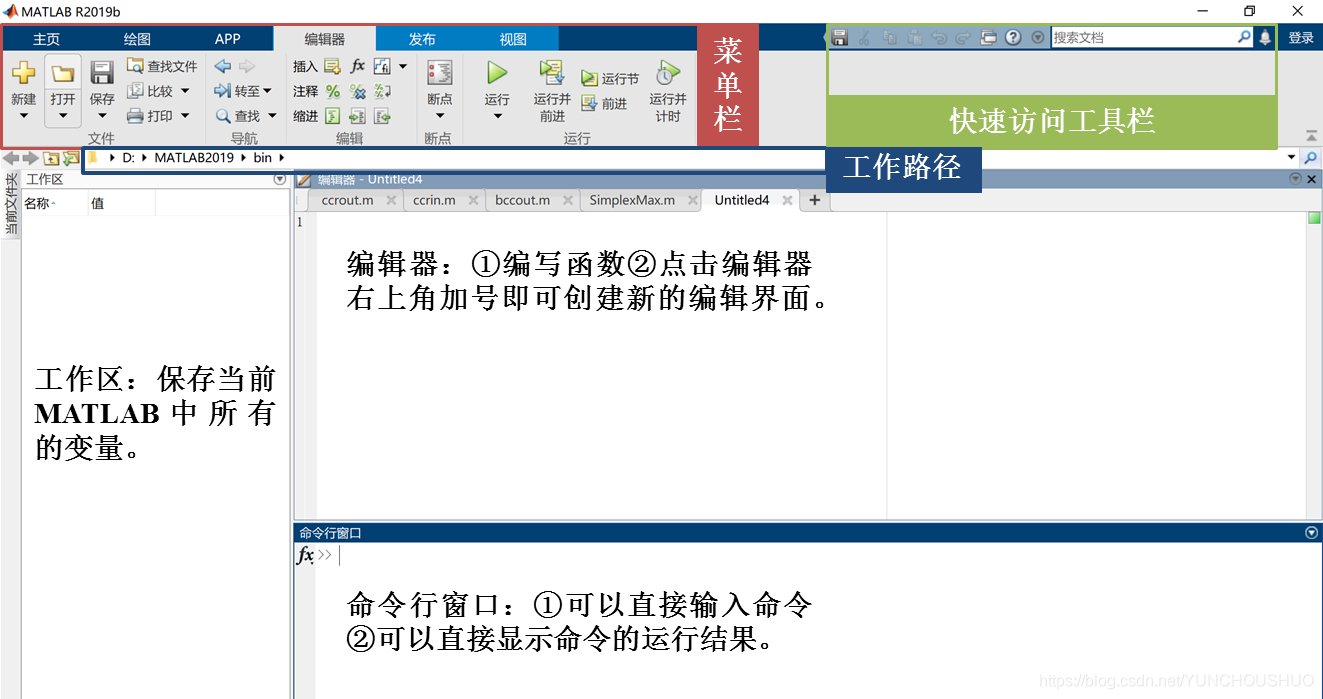
MATLAB作为目前最流行的科学计算软件之一,被广泛的应用于数据分析、无线通信、深度学习、量化金融与风险管理、控制系统等领域。为了让大家更好地使用该软件,小编在此对MATLAB界面进行简单的介绍:界面主要由菜单栏、快速访问工具栏、工作区、编辑器和命令行窗口五大功能区组成,各区的功能如下所示。
算法实现
在利用MATLAB平台进行算例测试之前,需要将线性规划问题转化为标准形式:

Matlab作为求解线性规划问题的主流工具之一,可以在网上找到很多相关的学习资源。此次,小编基于哈尔滨商业大学张敬信老师在知乎平台上分享的相关资源,与大家分享单纯形法以及其拓展算法(大M法和两阶段法)的MATLAB代码及相关算例的具体实现过程。
第一,在MATLAB编辑器窗口编写求解线性规划问题的通用函数—SimplexMax
function [x,z,ST,res_case] = SimplexMax(c,A,b,ind_B)
% 输入参数:c为目标函数系数,A为约束方程组系数矩阵,b为约束方程组常数项,ind_B为基变量索引;
%输出参数:x最优解, z为最优目标函数值,ST存储单纯形表数据,res_case=0表示有最优解,
res_case=1表示有无界解。
[m,n] = size(A);
%m存储约束条件个数
%n 存储决策变量个数
ind_N = setdiff(1:n, ind_B);
%非基变量的索引
ST = [];
format rat
% 使用分数表示数值
while true
% 循环求解
x0 = zeros(n,1);
x0(ind_B) = b;
%初始基可行解
cB = c(ind_B);
%计算cB
Sigma = zeros(1,n);
Sigma(ind_N) = c(ind_N) - cB*A(:,ind_N);
%计算检验数
[~, k] = max(Sigma);
%选出最大检验数,确定进基变量索引k
Theta = b ./ A(:,min(k));
%计算θ
Theta(Theta<=0) = 10000;
q=find(Theta== min(Theta));
%选出最小θ
el = ind_B(max(q));
%确定出基变量索引el:存在多个最小θ值时,
选择下标值最大的变量出基。
vals = [cB',ind_B',b,A,Theta];
vals = [vals; NaN, NaN, NaN, Sigma, NaN];
ST = [ST; vals];
if ~any(Sigma > 0)
%此基可行解为最优解, any存在某个>0
x = x0;
z = c * x;
res_case = 0;
return
end
if all(A(:,k) <= 0)
%有无界解
x = [];
res_case = 1;
break
end
% 换基
ind_B(ind_B == el) = k;
%新的基变量索引
ind_N = setdiff(1:n, ind_B);
%非基变量索引
A(:,ind_N) = A(:,ind_B) \ A(:,ind_N);
b = A(:,ind_B) \ b;
A(:,ind_B) = eye(m,m);
% 更新A和b
end第二,在MATLAB平台命令行窗口输入参数完成算例求解
1、单纯形法
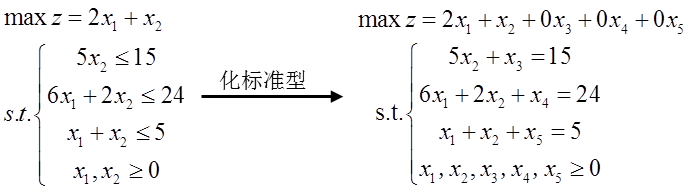
测试代码:
A = [0 5 1 0 0;6 2 0 1 0;1 1 0 0 1];
% A为约束方程组系数矩阵
b = [15;24;5];
%b为约束方程组常数项
c = [2 1 0 0 0];
% c为目标函数系数
ind = [3 4 5];
%ind_d为基变量索引
[x, z, ST, ca] = SimplexMax(c, A, b, ind)
%调用SimplexMax函数
%点击回车,命令行窗口便可输出结果。运行结果写入EXCEL:
xlswrite('SimplexTable1.xlsx', 'c', 1, 'C1');
% 写入Excel
xlswrite('SimplexTable1.xlsx', {'cB','xB', 'b'}, 1, 'A2');[~,n] = size(A);
X = strcat('x', string(1:n));
% 写表头
xlswrite('SimplexTable1.xlsx', X, 1, 'D2');
xlswrite('SimplexTable1.xlsx', c, 1, 'D1');
xlswrite('SimplexTable1.xlsx', ST, 1, 'A3');
% 写数值结果
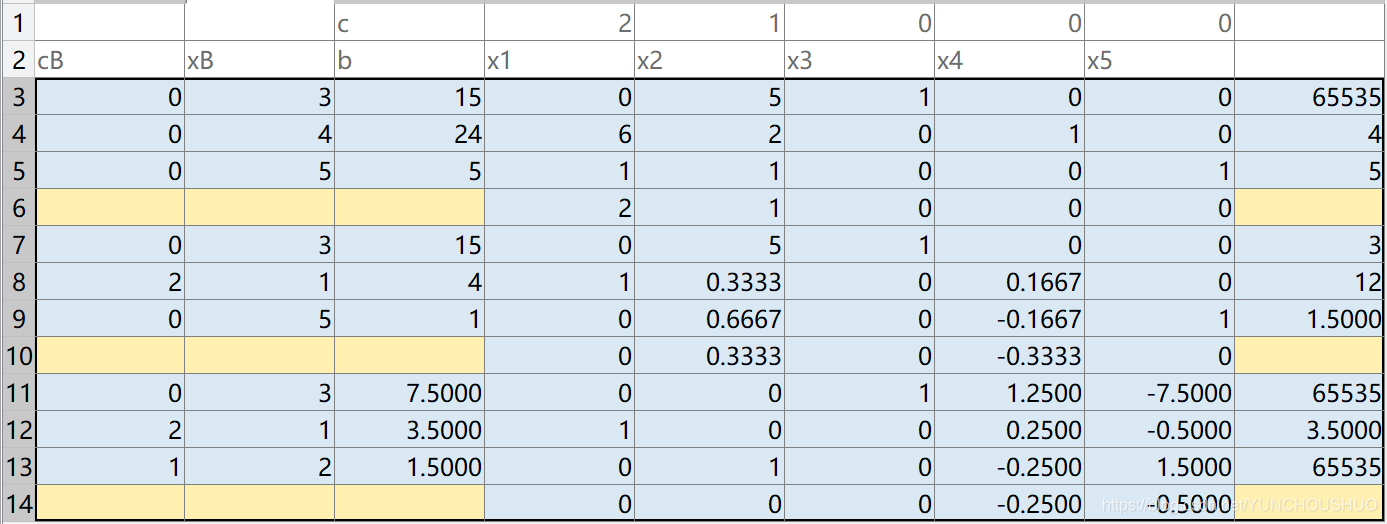
2、人工变量法
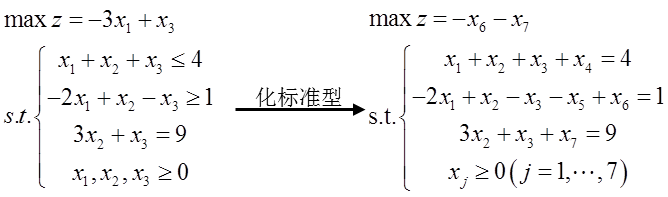
大M法的实现过程与单纯形法几乎一致,唯一的区别是需要设定一个无穷大的M值,然后在命令行窗口调用SimplexMax函数即可完成问题的求解。
测试代码:
M=10000;
% 假定M无穷大
A = [1 1 1 0 0;2 2 0 -1 1];
% A为约束方程组系数矩阵
b = [2;6];
% b为约束方程组常数项
c = [2 1 0 0 -M];
% c为目标函数系数
ind = [3 5];
%ind为基变量索引
[x, z, ST, ca] = SimplexMax(c, A, b, ind)
%调用SimplexMax函数
%点击回车,命令行窗口便可输出结果。

3、两阶段法
两阶段法就是需要调用两次SimplexMax,重点是需要做好两次函数调用之间的衔接工作。
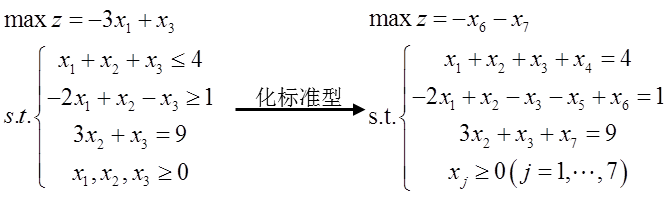
测试代码:
% 第一阶段
A1 = [1 1 1 1 0 0 0;-2 1 -1 0 -1 1 0; 0 3 1 0 0 0 1];
b1 = [4; 1; 9];
c1 = [0 0 0 0 0 -1 -1];
ind1 = [4 6 7];
[x1, z1, ST1, ca1] = SimplexMax(c1, A1, b1, ind1)
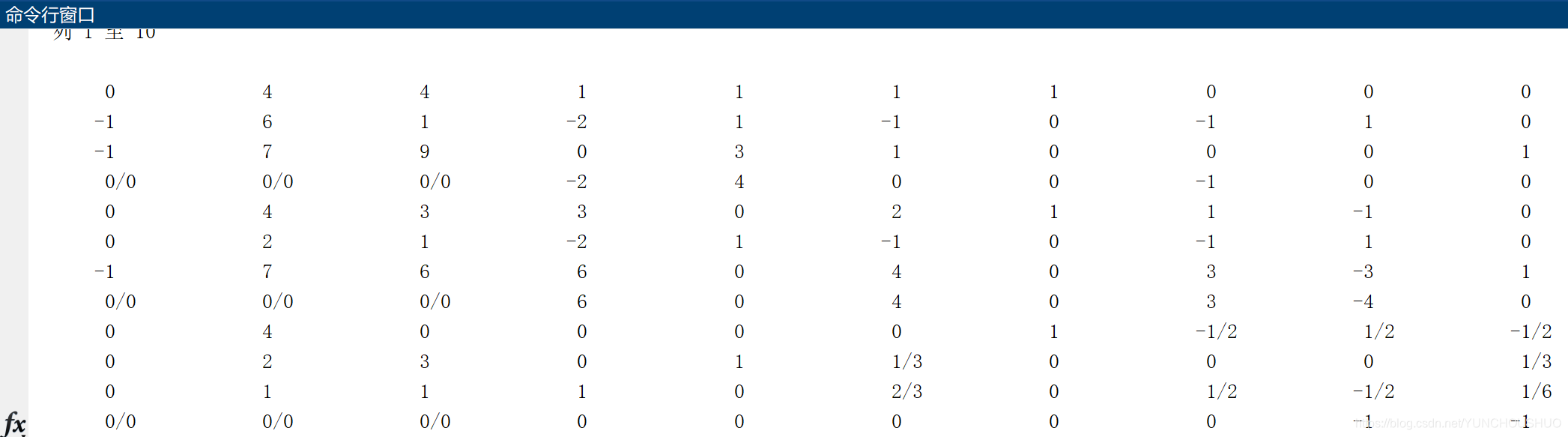
% 第二阶段,去除人工变量
A2 = ST1(end-size(A1,1):end-1,4:end-3); %2个人工变量, 2+1
b2 = ST1(end-size(A1,1):end-1,3);
c2 = [-3 0 1 0 0];
ind2 = ST1(end-size(A1,1):end-1,2)';
[x2, z2, ST2, ca2] = SimplexMax(c2, A2, b2, ind2)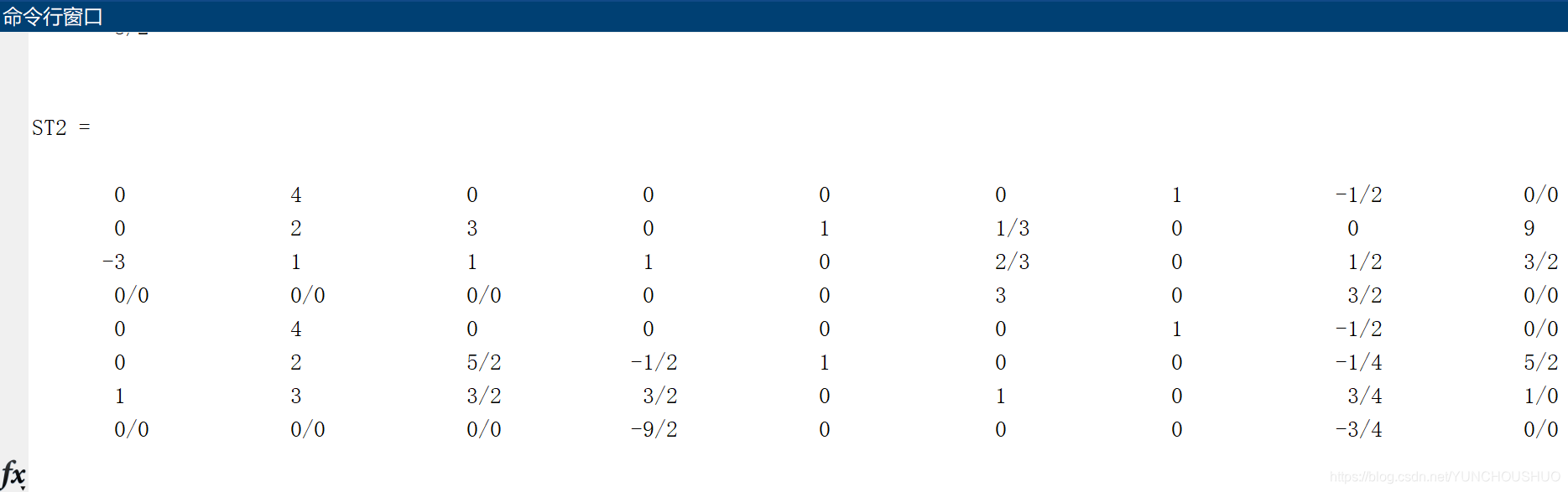
二、Excel求解
在做之前要先确保我们的电脑上安装的是Excel,WPS表格是没有这个功能的哦!然后需要安装规划求解的模块,步骤是“文件->选项->加载项->转到->勾选规划求解加载项->确定”,这样“数据”选项卡中就会出现“规划求解”这一项,然后我们就可以使用啦。

1、单纯形法
2、大M法
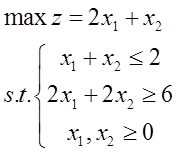
在EXCEL中,人工变量法和两阶段法的求解步骤同单纯形法。
3、两阶段法
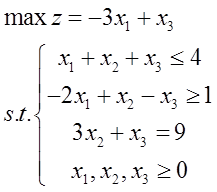
全文参考资料来源:
https://zhuanlan.zhihu.com/p/61466360
https://zhuanlan.zhihu.com/p/61575249
https://blog.csdn.net/zsz_shsf/article/details/52837063
作者|陈怡敏、曹贵玲
责编|何洋洋
审核|徐小峰

这篇关于运筹说 第20期 | 算法介绍之单纯形法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!