本文主要是介绍C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig与zag/左右双旋/3+4重构),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文目录
- 00.BBST——平衡二叉搜索树
- 01.AVL树
- 02.AVL的插入
- 2.1单旋——zig 与 zag
- 2.2插入节点后的单旋实例
- 2.3手玩小样例
- 2.4双旋实例
- 2.5小结
- 03.AVL的删除
- 3.1单旋删除
- 3.2双旋删除
- 3.3小结
- 04.3+4重构
- 05.综合评价AVL
- 5.1优点
- 5.2缺点
- 06.代码
- 注意
- 插入算法
- 删除算法
- 完整代码:AVL.h
00.BBST——平衡二叉搜索树
本文是介绍众多平衡二叉搜索树(BBST)的第一篇——介绍AVL树。故先来引入BBST的概念。由于上一篇介绍的二叉搜索树(BST)在极度退化的情况下,十分不平衡,不平衡到只朝一侧偏,成为一条链表,复杂度可达 O ( n ) O(n) O(n),所以我们要在“平衡”方面做一些约束,以防我们的树结构退化得那么严重。
具体来说,含 n n n个节点,高度为 h h h的BST,若满足 h = O ( l o g 2 n ) h=O(log_2 n) h=O(log2n),则称为称为平衡二叉搜索树。
01.AVL树
AVL树是一种BBST(稍后会证明)。它约束自己是否平衡,主要靠一个指标——平衡因子。定义:平衡因子=左子树高度-右子树高度。如果满足 − 2 < 全部平衡因子 < 2 -2<全部平衡因子<2 −2<全部平衡因子<2,则该AVL树处于平衡状态;否则,需要靠一系列措施,将其恢复平衡。
首先先证明AVL树满足BBST的要求,即 h = O ( l o g 2 n ) h=O(log_2 n) h=O(log2n)(下式)。我们可转而证明n=Ω(Φh)(即,AVL的节点数不会太少)

[结论] 高度为 h h h的AVL Tree 至少有 f i b ( ( h + 3 ) − 1 fib((h+3)-1 fib((h+3)−1 个节点
[证明]



02.AVL的插入
插入一个节点会导致一串祖先的失衡,删除一个节点至多导致一个祖先失衡。但是,通过后续代码就可发现,删除节点比插入节点复杂的多。原因是,插入节点只要调整好了一处,这条路径上的所有祖先都可平衡,复杂度是
O(1)。而删除节点是,调整好了一处平衡,另一处就会不平衡,自下而上层层调整,复杂度是O(n)。
2.1单旋——zig 与 zag
zig 与 zag 分别对应右单旋和左单旋。单旋的操作改变的是两个节点的相对位置。改变的是三条线:一上一下一子树。新树根上行指向原根,新树根原子树给到原根。如下图,V到Y那去,Y到C那去。

2.2插入节点后的单旋实例
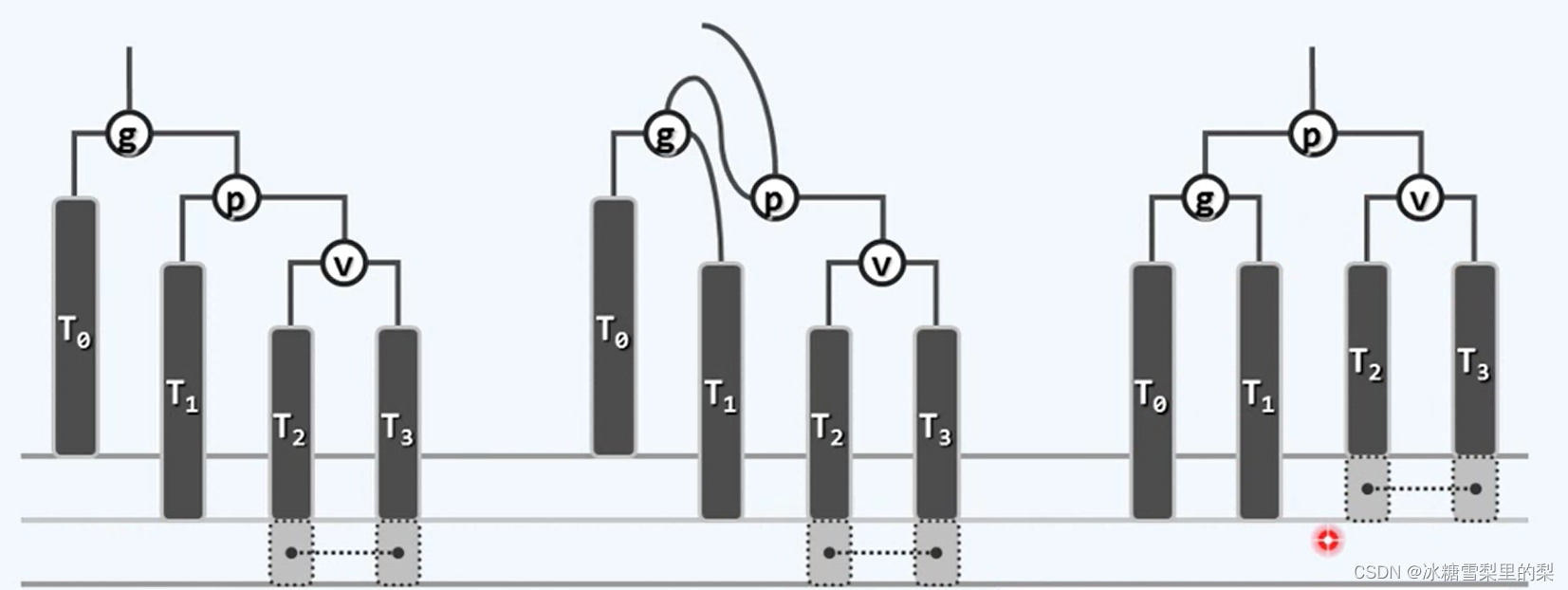
在下图 处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈一条线,而非“之”字,所以用单旋调整(之字形对应双旋)。具体来说,对g左单旋。
处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈一条线,而非“之”字,所以用单旋调整(之字形对应双旋)。具体来说,对g左单旋。
2.3手玩小样例
例题:将1,2,3,4,5,6依次插入空的AVL Tree,最终AVL Tree长成什么样?
[过程]首先正常插入1,2;插入3时,1是第一个发现不平衡的节点,zag(1),即对1进行左单旋,成功解决;正常插入4

插入5时,3是第一个发现不平衡的节点,zag(3),即对3进行左单旋,成功解决

插入6时,2是第一个发现不平衡的节点,zag(2),即对2进行左单旋,成功解决

2.4双旋实例
双旋的操作改变的是三个节点的相对位置。分为两种情况——zig-zag与zag-zig。
在下图 处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈“之”字,所以用双旋。具体来说,先zig§,再zag(g).
处添加一个节点,自上而下更新高度(或平衡因子),g会率先进入不平衡状态。观察g,p,v呈“之”字,所以用双旋。具体来说,先zig§,再zag(g).

2.5小结
AVL树中插入节点引发失衡,经旋转调整后重新平衡,此时包含节点g,p,v的子树高度是不变的,子树高度复原,更高祖先也必平衡,全树复衡。故在AVL树中修正插入节点引发的失衡不会出现失衡传播。
03.AVL的删除
删除一个节点至多导致一个祖先失衡。
3.1单旋删除

3.2双旋删除

3.3小结
AVL树中删除节点引发失衡,经旋转调整后重新平衡,此时包含节点g,p,v的子树高度有可能不变也有可能减小1,故在AVL树中修正删除节点引发的失衡有可能出现失衡传播。
04.3+4重构
通过观察以上插入和删除的结果示意图,发现结构是一样的——三个节点按顺序呈三角形,四个子树按原来的顺序分别挂在两个孩子节点的下边。(如下图)

那我们就不必关注具体的技巧了,而是将三个节点和四个子树拆开,像暴力组装魔方那样(先拆散)拼上。
template <typename T>
BinNode<T> * BST<T>::connect34(BinNode<T> * a, BinNode<T> * b, BinNode<T> * c, BinNode<T> * T1, BinNode<T> * T2, BinNode<T> *T3, BinNode<T> * T4)
{b->left = a; b->right = c;a->left = T1; a->right = T2;c->left = T3; c->right = T4;a->parent = b; c->parent = b;if (T1) T1->parent = a;if (T2) T2->parent = a;if (T3) T3->parent = c;if (T4) T4->parent = c;a->updateHigh(); b->updateHigh(); c->updateHigh();return b;
}template <typename T>
BinNode<T> * BST<T>::rotateAt(BinNode<T> * v)
{BinNode<T> * p = v->parent;BinNode<T> * g = p->parent;BinNode<T> * T1, *T2, *T3, *T4, *a, *b, *c;if (p == g->left && v == p->left){a = v; b = p; c = g;T1 = v->left; T2 = v->right; T3 = p->right; T4 = g->right;}else if (p == g->left && v == p->right){a = p; b = v; c = g;T1 = p->left; T2 = v->left; T3 = v->right; T4 = g->right;} else if (p == g->right && v == p->left){a = g; b = v; c = p;T1 = g->left; T2 = v->left; T3 = v->right; T4 = p->right;}else{a = g; b = p; c = v;T1 = g->left; T2 = p->left; T3 = v->left; T4 = v->right;}b->parent = g->parent; //向上链接return connect34(a, b, c, T1, T2, T3, T4);}
05.综合评价AVL
5.1优点
- 查找、插入、删除,最坏时间复杂度为 O ( l o g n ) O(logn) O(logn)
- O ( n ) O(n) O(n)的存储空间
5.2缺点
- 需要额外维护高度或平衡因子这一指标(后续Splay Tree可改善这一问题)
- 删除操作后,最多需旋转 Ω ( l o g n ) \Omega(logn) Ω(logn)次
- 单次动态调整后,全树拓扑结构的变化量可能高达 Ω ( l o g n ) \Omega(logn) Ω(logn) (RedBlack Tree可缩到 O ( 1 ) O(1) O(1))
谢谢观看~
06.代码
注意
fromParentTo()是根节点的情况connect34()向上链接别忘
插入算法
为什么不用现成的BST::insert(val)? BST::insert自带更新一串高度,旋转调整之后还得把这一串更新回来。
BinNode<T> * insert(T const & val){BinNode<T> * & X = BST<T>::search(val);if (!X){X = new BinNode<T>(val, BST<T>::hot); BinTree<T>::size++;BinNode<T> * X_copy = X;while (X_copy && AvlBalanced(X_copy)){X_copy->updateHigh();X_copy = X_copy->parent;}if (X_copy) //说明是因为遇到了不平衡节点才退出了while,现在解决不平衡问题{BinNode<T> * & tmp = BinTree<T>::fromParentTo(X_copy);tmp = BST<T>::rotateAt(tallerChild(tallerChild(X_copy))); // 内部自带单个节点更新高度}return X;}}
删除算法
受限于BST::remove的返回值仅仅是bool,所以用底层的removeAt. removeAt的返回值是接替者,但有时,接替者是NULL。还好有BST::hot,存放被删节点的父亲。实际上,BST::remove的更新高度也是从hot开始的
bool remove(T const & val) {BinNode<T> * & X = BST<T>::search(val);if (!X) return false;else{BST<T>::removeAt(X, BST<T>::hot);BinTree<T>::size--;// 与insert不同的是,remove可能要调整很多次for (BinNode<T> * g = BST<T>::hot; g; g = g->parent){int i = BF(g);if (!AvlBalanced(g)){BinNode<T> * & tmp = BinTree<T>::fromParentTo(g);tmp = BST<T>::rotateAt(tallerChild(tallerChild(g))); }else g->updateHigh();}return true;}}
完整代码:AVL.h
# pragma once
# include "BST.h"# define BF(x) (int)(getHigh(x->left) - getHigh(x->right))
# define AvlBalanced(x) ( -2 < BF(x) && BF(x) < 2 )template <typename T>
BinNode<T> * tallerChild(BinNode<T> * x)
{return (getHigh(x->left) > getHigh(x->right)) ? x->left : x->right;
}template <typename T>
class AVL :public BST<T>
{public:bool remove(T const & val) {BinNode<T> * & X = BST<T>::search(val);if (!X) return false;else{BST<T>::removeAt(X, BST<T>::hot);BinTree<T>::size--;// (可优化:直到到某祖先,高度不变,停止上行。那就要在刚刚更新高度时记录中途退出的位置,以便在此处判断)for (BinNode<T> * g = BST<T>::hot; g; g = g->parent){int i = BF(g);if (!AvlBalanced(g)){BinNode<T> * & tmp = BinTree<T>::fromParentTo(g);tmp = BST<T>::rotateAt(tallerChild(tallerChild(g))); // 内部自带单个节点更新高度}else g->updateHigh();}return true;}}BinNode<T> * insert(T const & val){BinNode<T> * & X = BST<T>::search(val);if (!X){X = new BinNode<T>(val, BST<T>::hot); //这一句话将两个关系连接BinTree<T>::size++;BinNode<T> * X_copy = X;while (X_copy && AvlBalanced(X_copy)){X_copy->updateHigh();X_copy = X_copy->parent;}if (X_copy) //说明是因为遇到了不平衡节点才退出了while,现在解决不平衡问题{BinNode<T> * & tmp = BinTree<T>::fromParentTo(X_copy);tmp = BST<T>::rotateAt(tallerChild(tallerChild(X_copy))); // 内部自带单个节点更新高度}return X;}}
};感谢观看~
附上前传:
C++数据结构之BinaryTree(二叉树)的实现
C++数据结构之BST(二叉搜索树)的实现
这篇关于C++数据结构之平衡二叉搜索树(一)——AVL的实现(zig与zag/左右双旋/3+4重构)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


