时隔3天，我终于理解了四个盘子的汉诺塔问题（Java实现）

目录

1.汉诺塔问题

2.思路讲解

2.1 一个盘子的情况。

2.2 两个盘子的情况

2.3 三个盘子的情况

3.四个盘子的汉诺塔问题

3.1 四个盘子的思路

3.2 实现代码来解决四个盘子的汉诺塔

1.汉诺塔问题

汉诺塔是啥大家都知道，汉诺塔的故事这里就不做介绍了，有读者感兴趣的可以去搜一搜，作者是用Java来实现的汉诺塔。

编程实现把 A 的 n 个盘子移动到 C

这是一个要使用递归解决的问题

要求：

• 每次只能移动1个盘子
• 大盘子只能放在小盘子下面

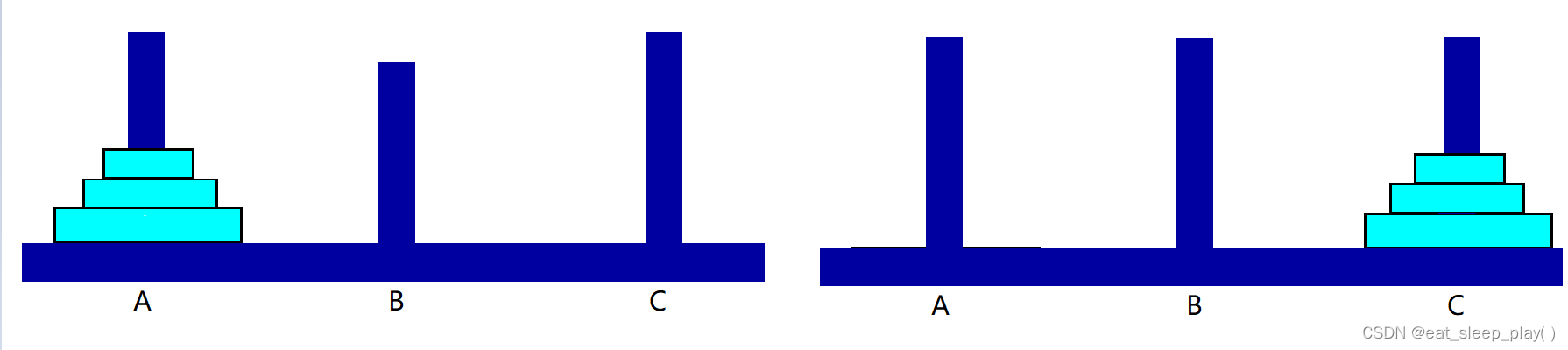
我们的目标是要解决4个盘子的汉诺塔问题，下面是移动完成的示意图

移动前：

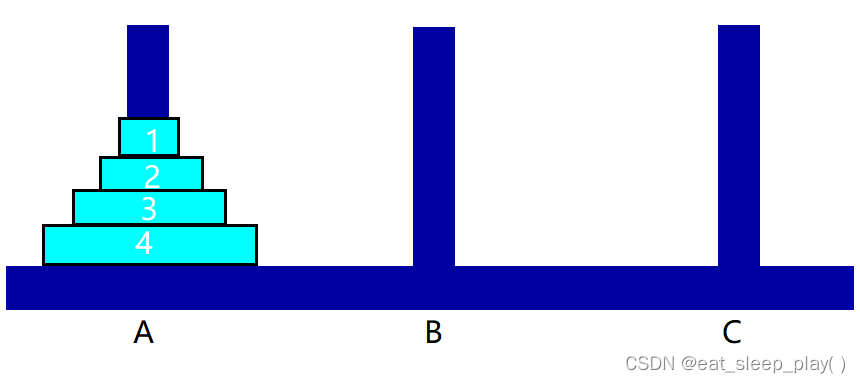
 移动后：

 动态演示图

2.思路讲解

2.1 一个盘子的情况。

如果是一个盘子，直接将A上的盘子移动到C即可。（一步）

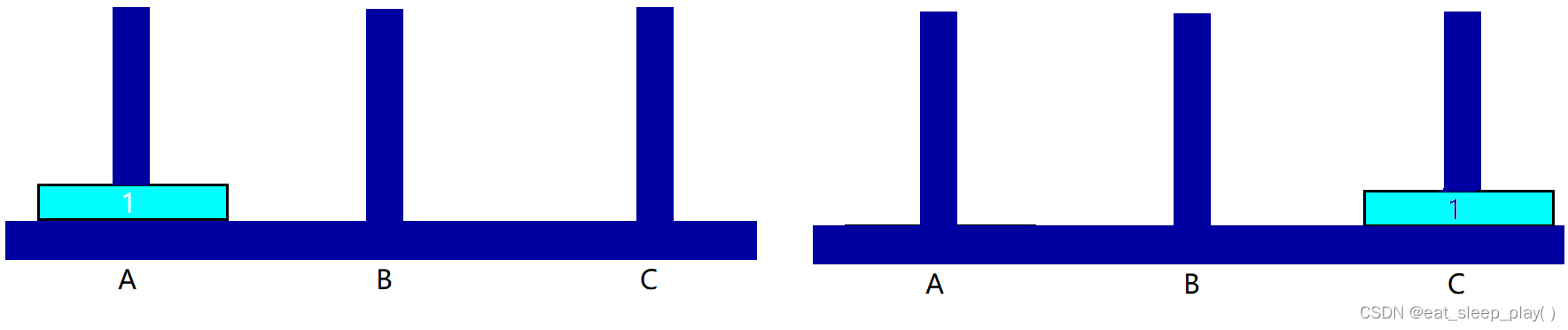
 步骤：A -> C

动态演示图

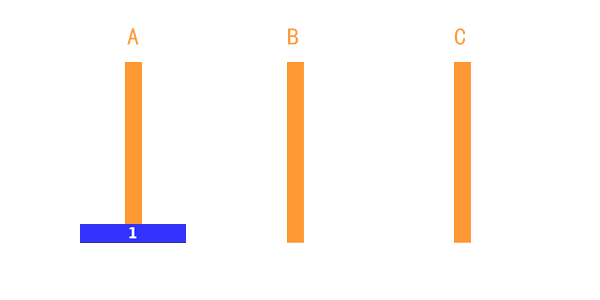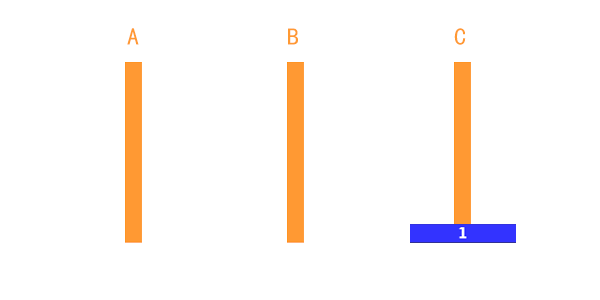
2.2 两个盘子的情况

如果是两个盘子，先将A上的小盘子移动到B上；再将A上的大盘子移动到C上，最后将B上的小盘子移动到C上即可。（三步）

步骤：A -> B    A -> C   B -> C

动态演示图

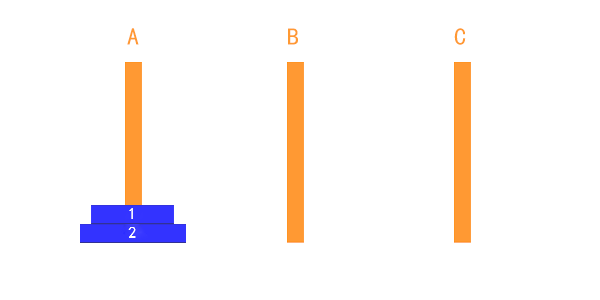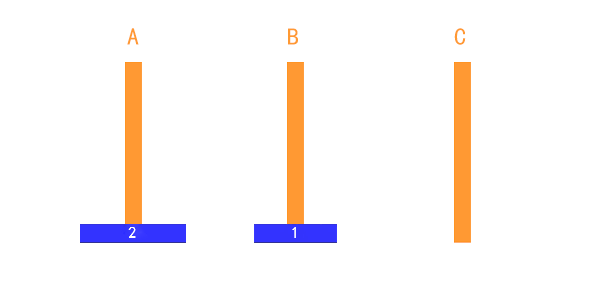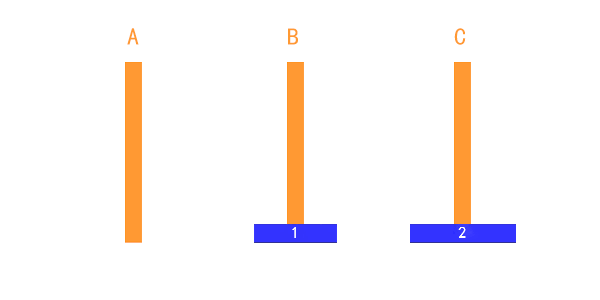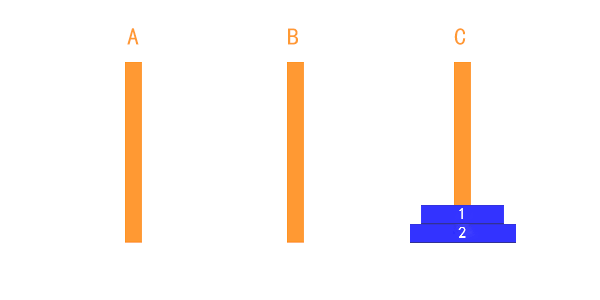
2.3 三个盘子的情况

如果是三个盘子，先将A上的盘子移动到C上；再将A上的盘子移动到B上，再将C上的盘子移动到B,再将A 上的盘子移动到C，再将上B的盘子移动到A，再将B的盘子移动到C，最后将A移动到C即可。（七步）

步骤：A -> C     A -> B     C -> B     A -> C     B -> A     B - > C     A -> C

动态演示图

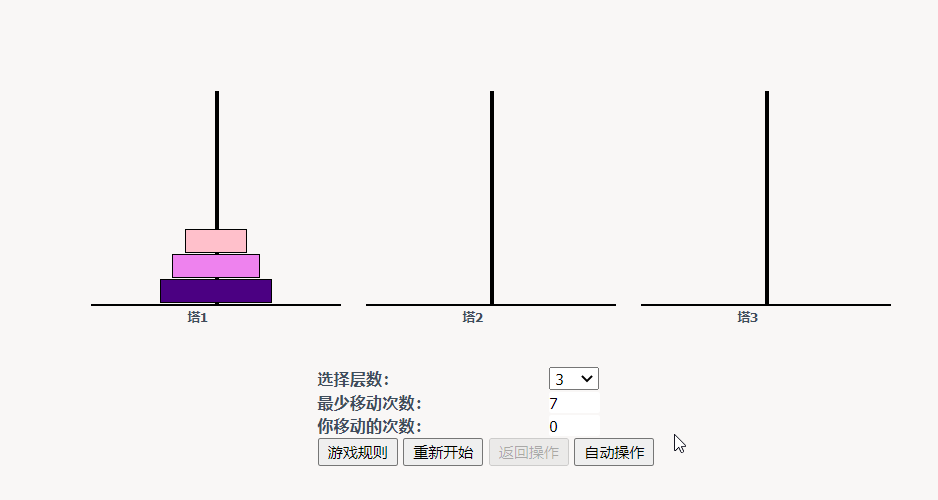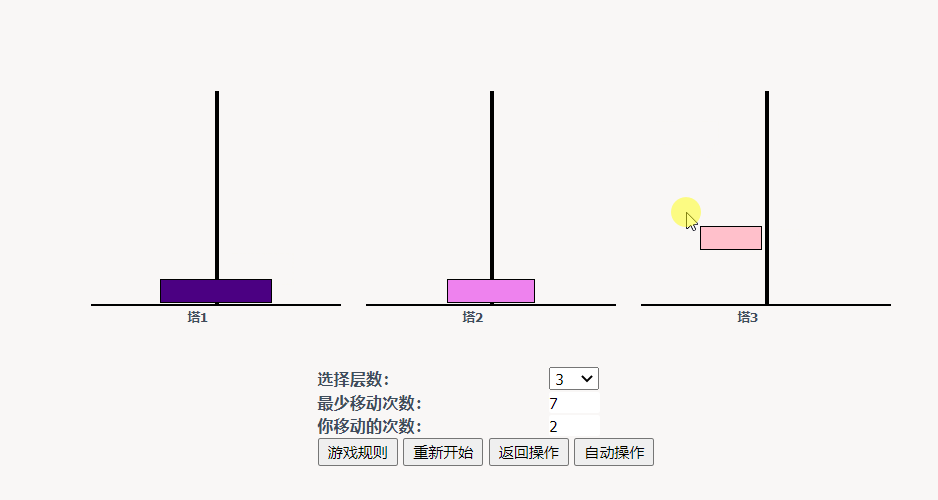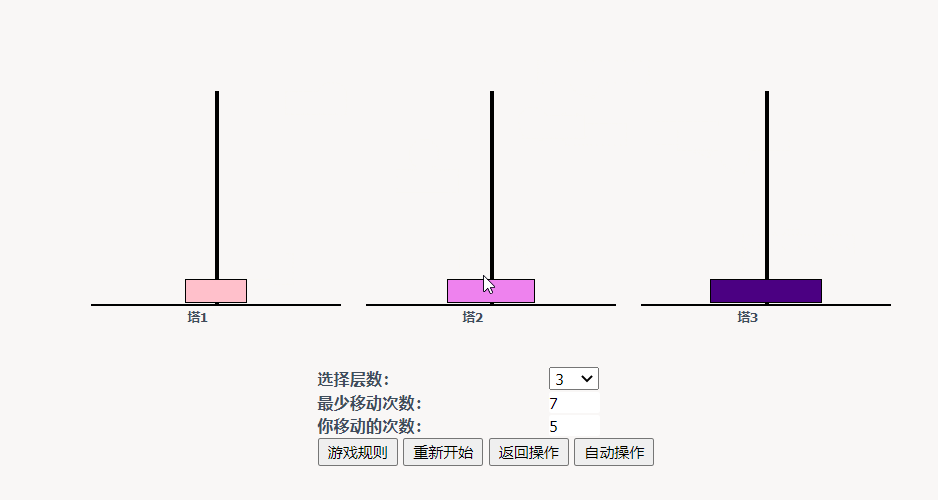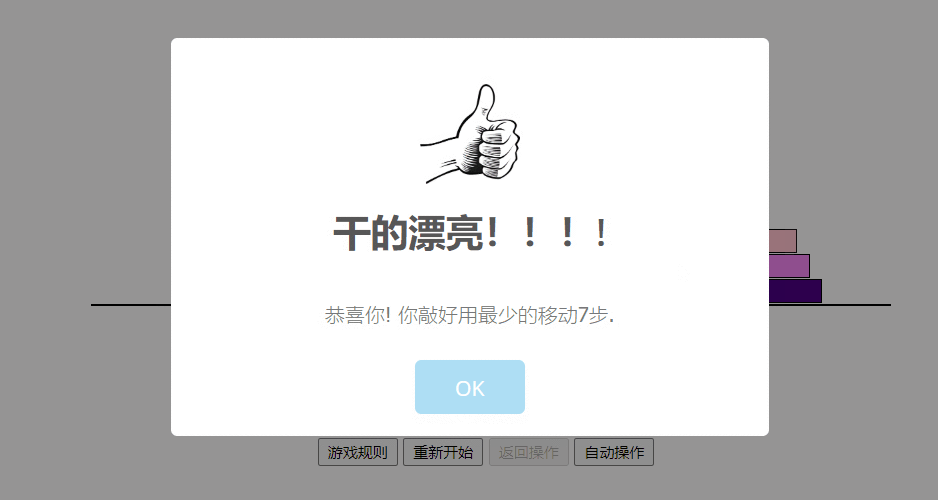
根据三个例子可以发现，除了只有一个盘子的情况。盘子在移动到C的过程中会有 n-1 个盘子在B上暂存。

两个盘子 n-1 就是会有一个盘子在B上暂存

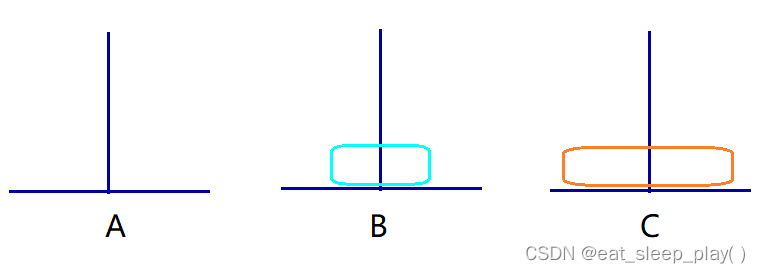
三个盘子 n-1 就是会有两个个盘子在B上暂存

所以解决四个盘子的方法就是先想办法把三个的盘子暂存到B上，再把最后一个盘子直接放到C上。对于B上的三的盘子，可以借用A逐步放到C上。

3.四个盘子的汉诺塔问题

3.1 四个盘子的思路

1. 借助C把 n-1 个盘子移动到B
2. 把A剩下的盘子移动到C
3. 借助A把 n-1 个盘子移动到C

3.2 实现代码来解决四个盘子的汉诺塔

    /*** @name 递归求解汉诺塔* @param start   起始位置* @param transit 中转位置* @param end     目标位置* **/public static void hanio(char start, char transit, char end, int number) {if (1 == number) {//只有一个盘子//直接将盘纸移动到Cmove(start, end);return;}else {//盘子大于1个//此时 transit 是目标位置；而 end 是中转位置hanio(start, end, transit, number - 1);//借助C将n-1个盘子移动到B上move(start, end);//此时 start 是中转位置，而end是目标位置hanio(transit, start, end, number - 1);//借助A把n-1个盘子移动到C上}}/*** @param start     起始位置* @param transit   目标位置**/public static void move(char start, char transit) {System.out.print(start +"->"+ transit + " ");}public static void main(String[] args) {hanio('A', 'B', 'C', 1);System.out.println();hanio('A', 'B', 'C', 2);System.out.println();hanio('A', 'B', 'C', 3);System.out.println();hanio('A', 'B', 'C', 4);}

代码结果：

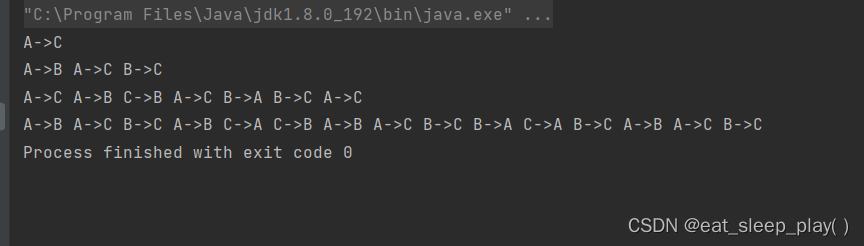
 前三行分别是1、2、3个盘子的移动过程，对照之前的思路讲解可以发现步骤没有错误。

第四行就是四个盘子的汉诺塔所需要的步骤。（十五步）