华容道问题求解_详细设计(四)之查找算法2

本文主要是介绍华容道问题求解_详细设计(四)之查找算法2_BFS，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

（续上篇）
利用BFS查找，会找到最短路径（没有权重的图），这个道理比较简单，这是由于寻找路径的方法都是从起点或者接近起点的位置开始的。查找过程如果画出图来，类似于一圈圈的放大，你可以想想是一个类似圆的渐开线的扫描过程。
前文已经谈到，这个BFS和DFS的主要不同就是对当前参数的保存方法不同，即BFS采用队列保存，DFS采用堆栈保存。因此，将DFS的保存当前参数的方法改成队列就可以实现BFS了。

BFS 核心代码

       internal bool SearchPathBFS(int endHashCode){if (statesObjQueue.Count == 0) return false;//##############################################################//## BFS 代码的改变如下                                        ##//##############################################################var lastState = DequeueState(); //var lastHashCode=   layoutHashCodeStk.Pop();// map it to the current  state MapToCurState(lastState);var curBestSteps = lastState.bestSteps+1;while (gameState.openPieces.Count > 0 && gameState.curOpenIdx < gameState.openPieces.Count)// There are open pieces not moved , move them one by one.{var selOpenPcs = gameState.openPieces[gameState.curOpenIdx];var selPcs = selOpenPcs.piece;var toPcs = selOpenPcs.MoveToPcs;var dirFrom = MoveToPcs(selPcs, toPcs);gameState.selPcs = selPcs;var redundant = RedundantState(gameState);StateShot stateShot = new StateShot(gameState, 0);// record the current best steps stateShot.bestSteps = curBestSteps;//Create the graph data structure AddEdgeToGraph(lastState, stateShot);if (gameState.curOpenIdx < lastState.openPcsArr.Length){gameState.curOpenIdx++;lastState.lastOpenIdx = gameState.curOpenIdx;}if (!redundant.Item1){SearchOpenPieces();stateShot = new StateShot(gameState, 0);stateShot.bestSteps = curBestSteps;//##############################################################//## BFS 代码的改变如下                                       ##//##############################################################         EnqueueState(lastState, stateShot, selPcs, toPcs);//add edge to the grapph and enqueue the current state}// 2024-01-30 Found the least steps with BFS and it runs very fast.// Judge if it succeeds that caocao is at the exit of the board.if (endHashCode==0 && selPcs.type == 4){if (selPcs.hrdPos.X == 2 && selPcs.hrdPos.Y == 4){RefreshLayout();Application.DoEvents();var verTex = GetMyHashCodeV1(gameState);// the layout might not the same that needs to record all of them if (!endVtxLst.Contains(verTex)) endVtxLst.Add(verTex);//MessageBox.Show(string.Format("Success! The best steps is {0},the hash code is {1}", hCodeAndShotShortPathDict[verTex].Item2, verTex));//return false;//debug}}else if (redundant.Item2 == endHashCode){RefreshLayout();Application.DoEvents();var verTex = GetMyHashCodeV1(gameState);// the layout might not the same that needs to record all of them if (!endVtxLst.Contains(verTex)) endVtxLst.Add(verTex);}MapToCurState(lastState); // back the last state and try to moev next open pieces}return true;}

和DFS的代码对比一下就会发现，除了堆栈改成队列之外，代码几乎没有做什么改变。

下面给出两个主要变化的函数代码
入队代码：

       private void EnqueueState(StateShot source, StateShot dest, Piece selPcs, Piece dstPcs){statesObjQueue.Enqueue(dest);var toHashCode = GetMyHashCode(dest);stateHashCodeLst.Add(toHashCode);int[,] layoutArr = new int[6, 7];Array.Copy(dest.layoutOfIdx, layoutArr, layoutArr.Length);hCodeAndShotDict.Add(toHashCode, (dest.basePcs, selPcs.idx, dstPcs.idx));var frmHashCode = GetMyHashCode(source);AddEdge(frmHashCode, toHashCode, 1);}

出队代码

       private StateShot DequeueState(){var stshot = statesObjQueue.Dequeue();//stateHashCodeStack.Pop();return stshot;}

其中 statesObjQueue 的定义为;

//used to store the game state and the shortest path from last state For BFS search private Queue<StateShot> statesObjQueue= new Queue<StateShot>();

运行之后，就很快找到了最少步数，虽然在过程当中也构建了一个图，但是并没有使用这个图。

结果也比较理想，是一个对称的结果，符合预期。这个原因，我想是因为在BFS 的求解过程当中的每一次探索的步数的基数都是一样的，而路径是不同的，因此也就必然会出现这么一种结果。
运行结果获得30种符合要求的布局，根据对称性，应该是15 中不同的解法。
截图如下：
说明：左面列表数值是该布局对应的Hash值
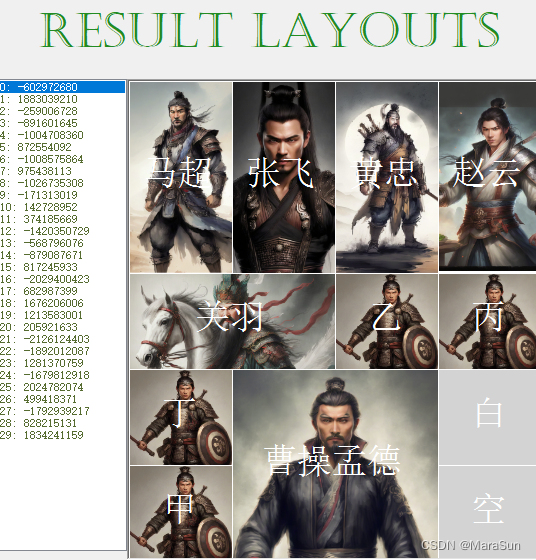
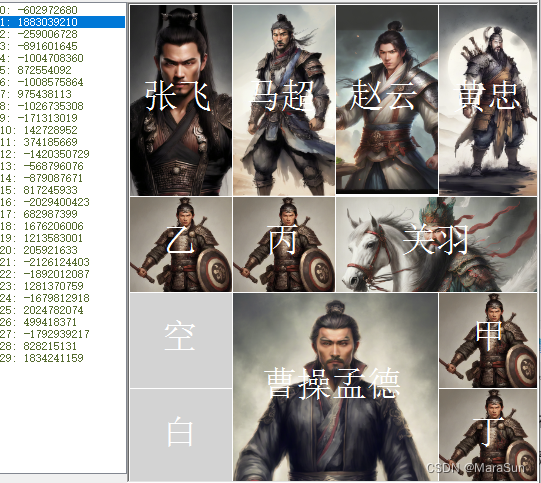
在这里插入图片描述

对比上面的布局，发现这是个对称的布局。这些解法中，最少的是81步，最多的是 115步。
其余结果请参考下列视频。另外 “不同解法 ”的含义就是最终的布局不同。