随机森林 bagging袋装法(基于bootstrap重抽样自举法)的原理与python实现—

本文主要是介绍随机森林 bagging袋装法(基于bootstrap重抽样自举法)的原理与python实现——机器学习笔记之集成学习 Part 1，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

* * * The Machine Learning Noting Series * * *

⚫袋装法和随机森林过程基本一样，都是根据bootstrap的一系列样本分别建立决策树，然后用这些决策树投票出结果。最大区别，也就是随机森林更好的原因在于：随机森林在建立决策树时的分组变量存在随机性。

⚫建立大量模型进行投票得出的估计为真值的无偏及一致估计，由此得到的测试误差也是泛化误差真值的无偏估计。

1 Bootstrap重抽样自举法

🍿🍿🍿Bootstrap重抽样自举法的原理与python实现的详细说明，点击参考我的这篇文章。简单介绍：

概念：重抽样自举法（Bootstrap）也叫做自助抽样法或者0.632自举法。

方法：对N个样本，进行B次有放回的重抽样形成B个样本，每个样本包含N个数据。

0.632？：每个样本，每次抽样被抽到的概率为1/N，抽不到的概率为1-1/N，因此N次均未被抽到的概率为 $\left ( 1-\frac{1}{N} \right )^{N}\approx \frac{1}{e}= 0.368$ ，故整体上也有1-36.8%=63.2%的样本可作为自举样本。

作用：用于估计统计量的标准误（srandard error），比如回归中回归系数的标准误。

2 袋装法（Bagging）

说明：袋装法Bagging 为Bootstrap Aggregating 的缩写，在单个学习器（基于单个bootstrap样本构建的模型，这里是决策树，也可以是贝叶斯分类器，K-邻近等模型）具有高方差和低偏差时很有效。

方法：

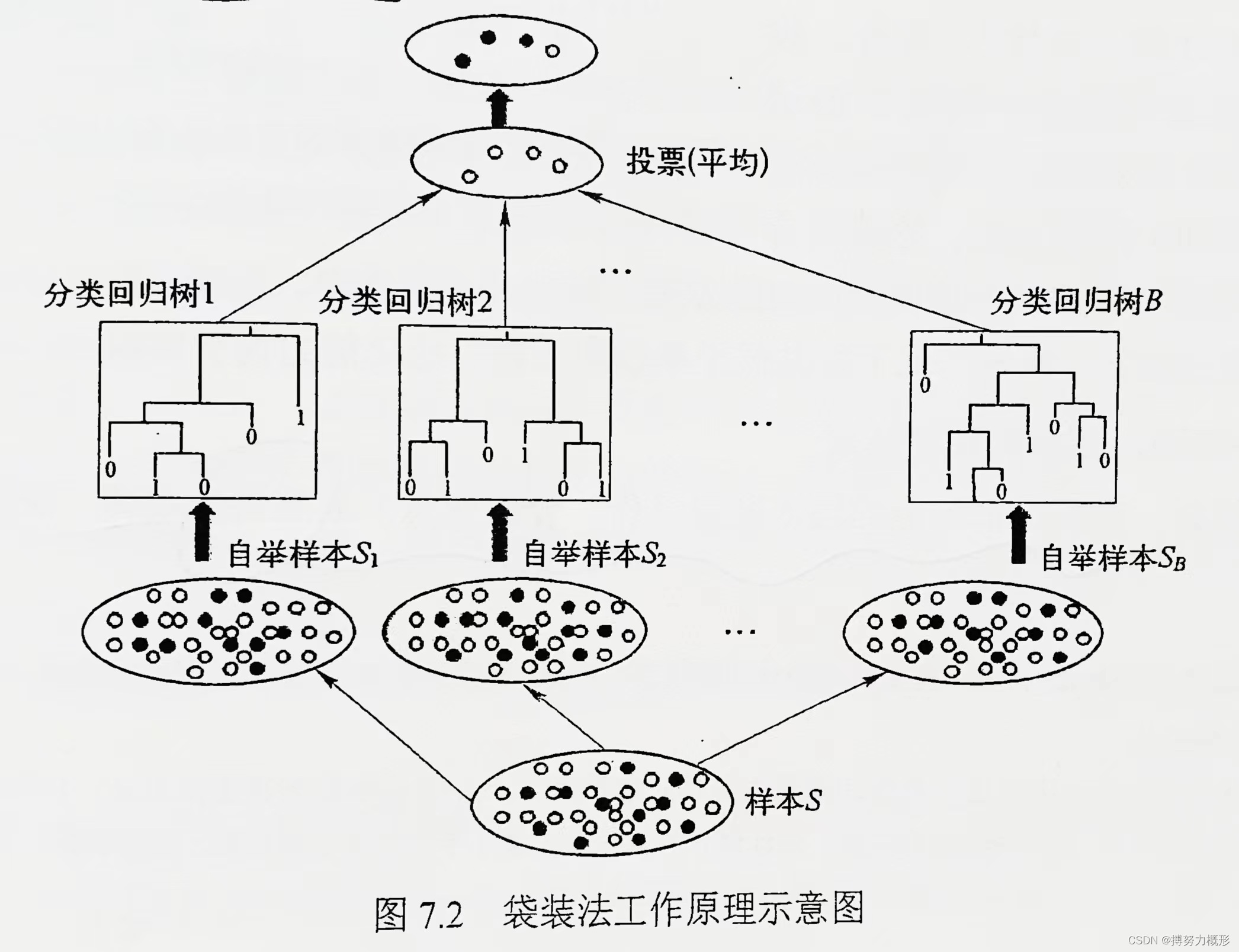
测试误差的估计：

应对每个样本观测，得到其作为OOB时基础学习器所给出的预测结果。即若样本观测在建模过程中有q次作为OOB观测，则只有q个基础学习器提供预测值，最终预测结果是这个q值的均值或投票。
袋装法可方便的计算出OOB测试误差，而不必再用其他样本划分方法。
自举次数越多，即建立的估计模型越多，越有助于降低方差，消除测试误差计算结果的随机性。

输入变量重要性的度量：

基于多棵树计算输入变量重要性：计算B棵树异质性下降总和，总和的最大值对应的输入变量重要性最高。

3 随机森林

原理：独立同分布的B个预测值（由上文的B个学习器产生） $Z_{i},i=1,2,...,N$ ，若其方差为 $\sigma ^{2}$ ，两两相关系数为 $\rho$ ，那么投票结果，即Z的均值的方差为：

$Var\left (\overline{Z} \right )=Var\left ( \frac{1}{N} \sum_{i=1}^{N} Z_{i}\right ) = \frac{1}{N} \left [ N\sigma ^{2}+N(N-1))\rho \sigma ^{2} \right ]=\frac{\sigma ^{2}+(N-1)\rho \sigma ^{2}}{N}=\rho \sigma ^{2}+\frac{1-\rho }{N}\sigma ^{2}$

袋装法通过增加B来减少方差（上式结果后半部分），在此次基础上，随机森林则进一步通过减少相关性（降低树间的相似性）来降低方差（上式结果前半部分）。

随机森林的随机体现在：①样本随机性，来自于Bootstrap的随机抽样；②属性随机性，树的生成随机选择分类属性。

方法：

输入变量重要性的度量：

基本思路是，若某个变量影响力大，那么同样的随机噪声，该变量随模型OBB结果影响更大。为了测度重要性，首先计算 $\widehat{T}^{*(b)} \left ( b=1,2,...,B \right )$ 的OOB测试误差，记为 $e\left (\widehat{T}^{*(b)} \right )$ 。为了测度第j个输入变量对输出变量的重要性：

1）随机打乱 $\widehat{T}^{*(b)}$ 的OOB在第j个输入变量上的取值顺序，重新计算 $\widehat{T}^{*(b)}$ 基于OOB的测试误差，记为 $e^{j}\left (\widehat{T}^{*(b)} \right )$ .

2）计算第j个输入变量添加噪声后 $\widehat{T}^{*(b)}$ 的OOB误差的变化： $c_{\widehat{T}^{*(b)}}^{j}=e^{j}\left (\widehat{T}^{*(b)} \right )-e\left (\widehat{T}^{*(b)} \right )$ .

重复上述步骤B次，得到B个 $c_{\widehat{T}^{*(b)}}^{j},( b=1,2,...,B )$ ，计算其均值 $\frac{1}{B}\sum_{b=1}^{B}c_{\widehat{T}^{*(b)}}^{j}$ ，这就是第j个输入变量添加噪声后随机森林的OOB误差的变化，该误差值越大，表明变量越重要。

随机森林和袋装法的比较：

在输入变量较多的情况下，随机森林的优势会更加明显。下图为4个输入变量时不同方法的测试误差变化情况，可以看出随着树数的增加，随机森林的误差最小。具体可见下面的python实例。

4 python实现——一个实例

下面的例子同时实现袋装法和随机森林，并比较其性能。该例子为PM2.5浓度的回归预测，需要数据可向我索要。

#本章需导入的模块
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings(action = 'ignore')
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']  #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
from sklearn.model_selection import train_test_split,KFold,cross_val_score
from sklearn import tree
import sklearn.linear_model as LM
from sklearn import ensemble
from sklearn.datasets import make_classification,make_circles,make_regression
from sklearn.metrics import zero_one_loss,r2_score,mean_squared_error
import xgboost as xgb

# 准备数据
data=pd.read_excel('北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
data=data.loc[(data['PM2.5']<=200) & (data['SO2']<=20)]
X=data[['SO2','CO']]
Y=data['PM2.5']
X0=np.array(X.mean()).reshape(1,-1)

# 运行袋装法和随机森林
modelDTC = tree.DecisionTreeRegressor(max_depth=5,random_state=123)
dtrErr=1-cross_val_score(modelDTC,X,Y,cv=10,scoring='r2')
BagY0=[]
bagErr=[]
rfErr=[]
rfY0=[]
for b in np.arange(10,200):Bag=ensemble.BaggingRegressor(base_estimator=modelDTC,n_estimators=b,oob_score=True,random_state=123,bootstrap=True)Bag.fit(X,Y)bagErr.append(1-Bag.oob_score_)BagY0.append(float(Bag.predict(X0)))RF=ensemble.RandomForestRegressor(n_estimators=b,oob_score=True,random_state=123,bootstrap=True,max_features="sqrt")RF.fit(X,Y)      rfErr.append(1-RF.oob_score_)     rfY0.append(float(RF.predict(X0)))

# 可视化结果
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(12,4))
axes[0].axhline(y=dtrErr.mean(),linestyle='-.',label='回归树')
axes[0].plot(np.arange(10,200),bagErr,linestyle='-',label='Bagging回归树(方差=%.3f)'%np.var(BagY0))
axes[0].plot(np.arange(10,200),rfErr,linestyle='--',label='随机森林(方差=%.3f)'%np.var(rfY0))
axes[0].set_title("回归树、Bagging回归树和随机森林")
axes[0].set_xlabel("树的棵树B")
axes[0].set_ylabel("测试误差")
axes[0].legend()axes[1].barh(y=(1,2,3,4),width=RF.feature_importances_,tick_label=X.columns)
axes[1].set_title("输入变量的重要性")
for x,y in enumerate(RF.feature_importances_):    axes[1].text(y+0.01,x+1,'%s' %round(y,3),ha='center')

结果如下图所示，可以看出，当输入变量较多时，随着树数的增加，随机森林的优势逐渐显现，测试误差更低。