全连接神经网络算法原理(激活函数、前向传播、梯度下降法、损失函数、反向传播)

本文主要是介绍全连接神经网络算法原理(激活函数、前向传播、梯度下降法、损失函数、反向传播)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

全连接神经网络是学习深度学习的基础，其中最重要的原因是，全连接神经网络利用了反向传播算法进行参数更新，使得神经网络可以通过不断喂给数据进行参数更新达到不断学习的目的，反向传播算法是梯度下降法在深度神经网络上的具体实现方式。反向传播算法其原理就是利用梯度下降法来不断更新神经网络的参数，目前几乎所有的神经网络参数的更新的方式都是利用的梯度下降法或者经过优化的梯度下降法。
  
神经网络可以帮助我们做什么呢？目前可以解决两类任务，分类任务和回归任务：

• 分类任务就是对输入的数据特征进行学习，输出是对应输入数据预测类别，比如输入一些猫和狗的数据并对其进行学习，现在输入一张新的图片，判断图中的图片是否是猫还是狗；
• 回归任务就是对输入的数据特征进行学习，输出是对应输入数据的预测值，比如输入历史的天气数据相关特征进行学习，现在输入一段历史的天气数据相关特征数据，输出第二日的温度预测值；

1、全连接神经网络的整体结构：

全连接神经网络模型是由输入层、隐藏层、输出层所组成，全连接神经网络结构如下图所示：

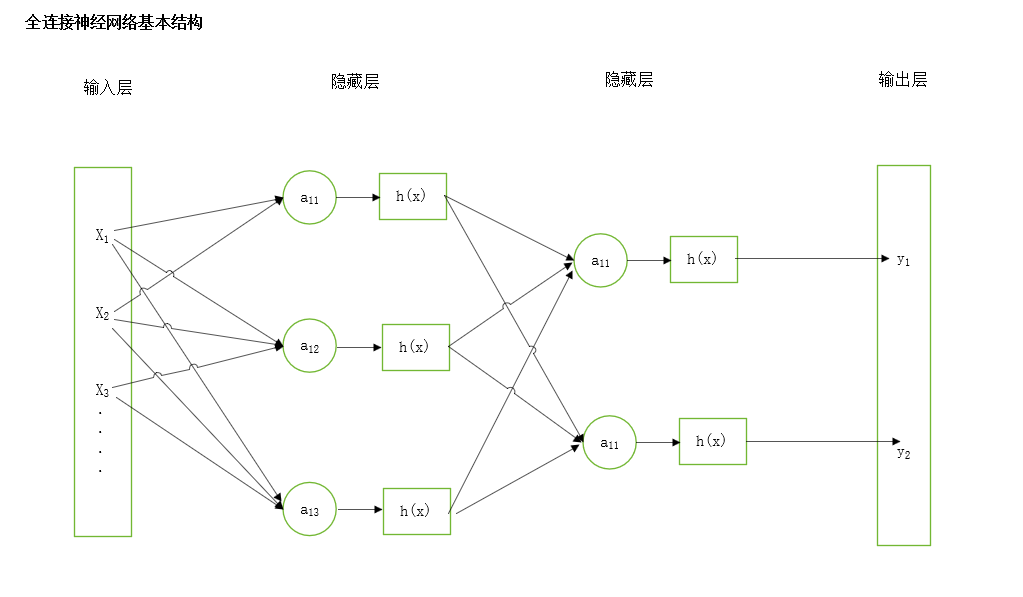
全连接神经网络的每一层都是由一个一个的神经元所组成的，因此只要搞清楚神经元的本质就可以搞清楚全连接神经网络了。如图下所示，这是一个全连接神经网络神经元的模型图：

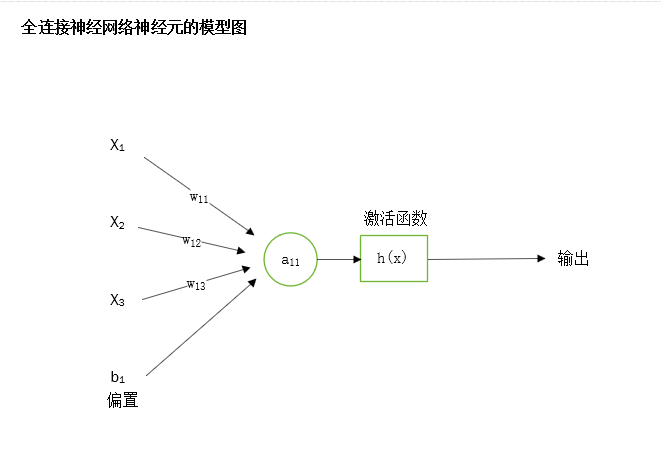
该神经元的数学表达式：a = h( w∗x + b )

• b为偏置，用于控制神经元被激活的容易程度;
• w表示各个信号的权重，用于控制各个信号的重要性；
• h()为激活函数，是一种非线性函数；

为什么神经网络都要加上激活函数，同时该激活函数为什么要一定是非线性的呢？

如果神经网络中没有使用非线性激活函数，无论堆叠多少层神经元，整个网络的输出都将是输入的线性组合，这样多层神经网络将等同于单层神经网络，无法发挥多层网络带来的优势；

2、激活函数

在神经网络中比较常用的激活函数有Sigmoid函数、Tanh函数、ReLU函数、Leaky ReLU函数、softmax函数；

2.1、Sigmoid函数

Sigmoid函数最早是在逻辑回归中提到的，它作为解决二分类的问题出场。其值域是在[0,1]之间，输出的值可以作为分类的概率。

Sigmoid函数的公式和导数如下式所示：

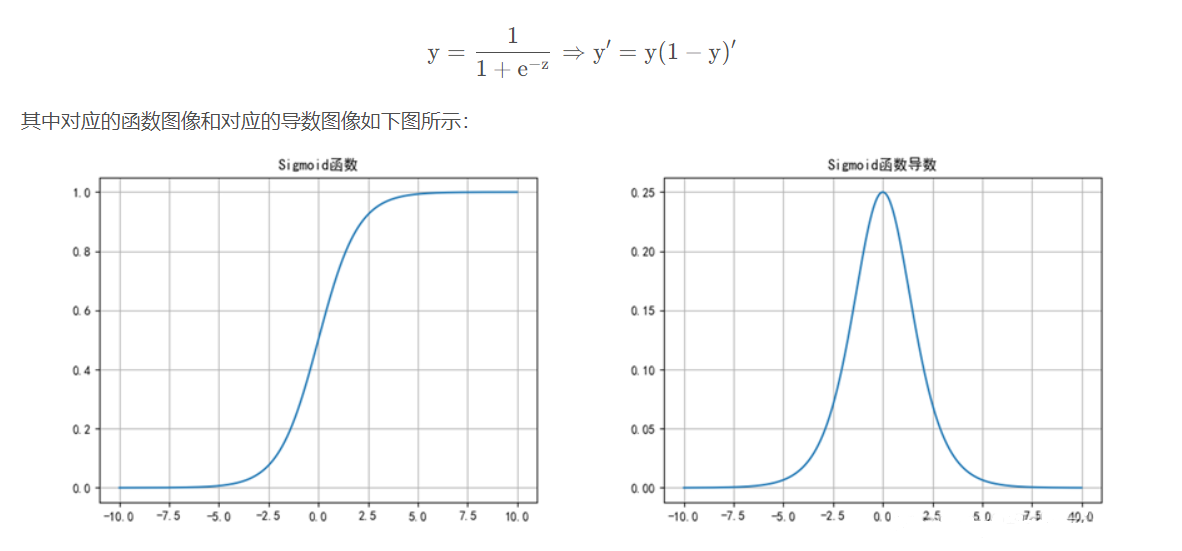
Sigmoid函数优点：
  1、简单、非常适用分类任务；
Sigmoid函数缺点：
  1、反向传播训练时有梯度消失的问题；
  2、输出值区间为(0,1)，关于0不对称；
  3、梯度更新在不同方向走得太远，使得优化难度增大，训练耗时；

2.2、Tanh函数

函数表达式和其对应的导数表达式如下式所示：

Tanh函数，其输出值在区间 [-1, 1]

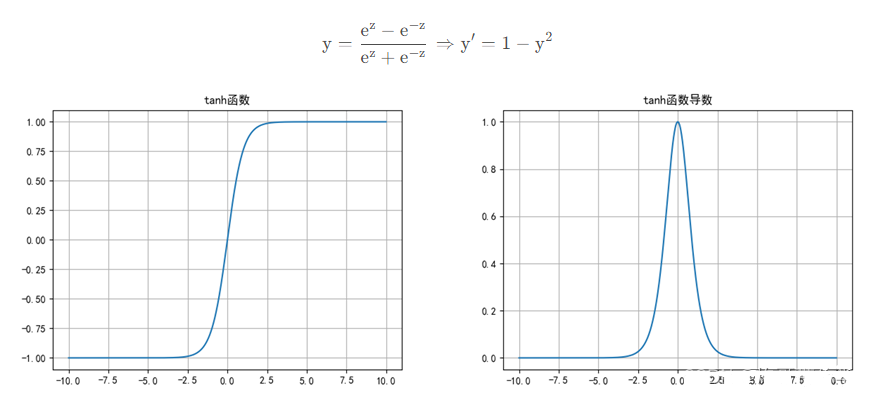
Tanh函数优点：
1、解决了Sigmoid函数输出值非0对称的问题；
2、训练比Sigmoid函数快，更容易收敛；
Tanh函数缺点：
1、反向传播训练时有梯度消失的问题；
2、Tanh函数和Sigmoid函数非常相似；

2.3、ReLU函数

ReLU函数是目前在神经网络使用最流行的激活函数。其函数表达式和其对应的导数非常简单：

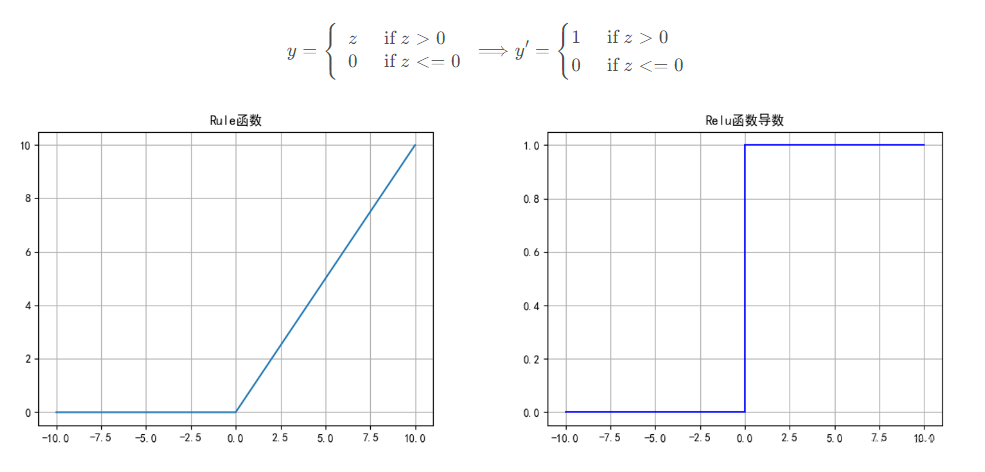
ReLU函数优点：
  1、解决了梯度消失的问题；
  2、计算更为简单，没有Sigmoid函数和Tanh函数的指数运算；
ReLU函数缺点：
  1、训练时可能出现神经元死亡；

2.4、Leaky ReLU函数

Leaky ReLU函数是ReLU函数的变体。其函数和对应导数的表达式为：

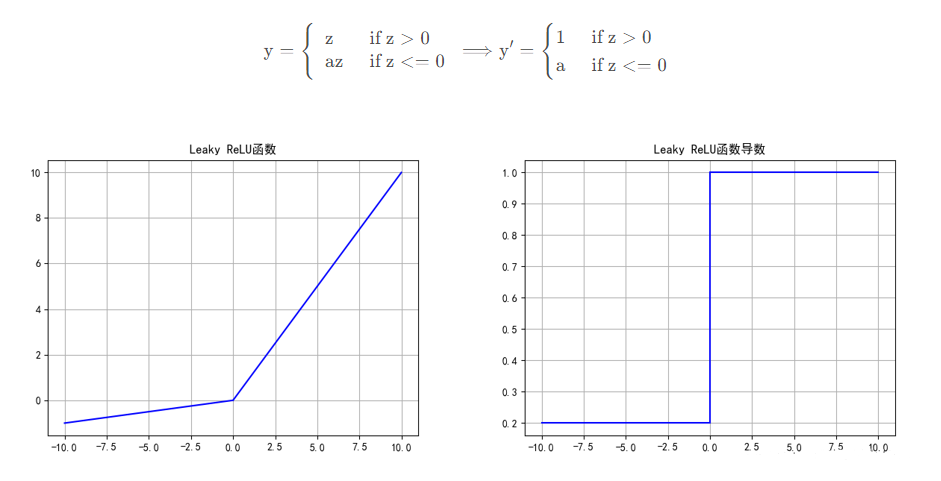
Leaky ReLU函数优点：
  1、解决了ReLU的神经元死亡问题；
Leaky ReLU函数缺点：
  1、无法为正负输入值提供一致的关系预测（不同区间函数不同）；

2.5、SoftMax激活函数

SoftMax函数通常被用在多分类网络模型中，其表达式如下：

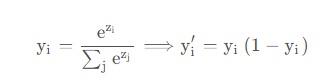
SoftMax函数的值域是在[0,1]之间的，并且存在多个输出，例如是一个5分类的任务，那么SoftMax函数最终的输出是对应每个类别的的概率，同时这5个类别对应的概率相加最终的结果为1。因此在多分类任务的场景下，神经网络的最后一层一般都是使用SoftMax函数来作为激活函数。

3、前向传播

神经网络的输出是通过前向传播最后输出的，前向传播是将数据特征作为输入，输入到隐藏层，将数据特征和对应的权重相乘同时再和偏置进行求和，将计算的结果通过激活函数进行激活，将激活函数输出值作为下一层神经网络层的输入再和对应的权重相乘同时和对应的偏置求和，再将计算的结果通过激活函数进行激活，不断重复上述的过程直到神经网络的输出层，最终得到神经网络的输出值。

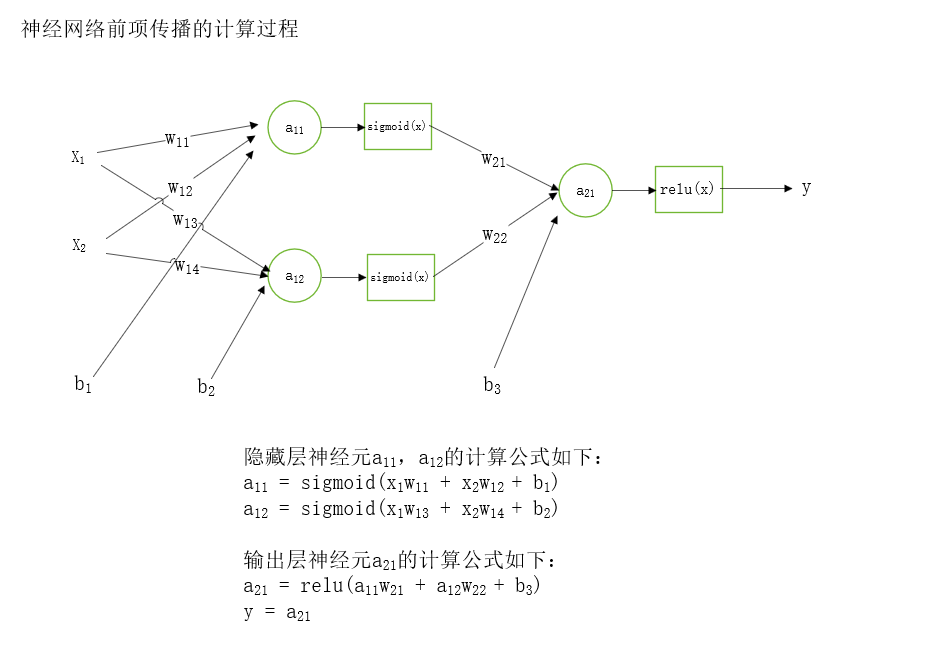
4、损失函数：

损失函数：我们要计算所有数据真实值和输出值之间的误差和并计算出平均值，这个函数称为均方误差函数，也是线性回归模型的损失函数；

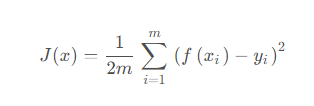
5、梯度下降法：

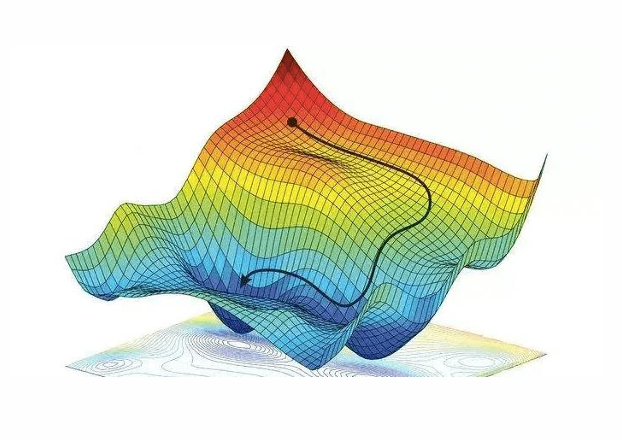
场景：在一个漆黑的夜晚，一个人要下山，但是他完全看不到周围的环境，只能通过手去感知。因此这个人就想到一个办法，朝着自己的四周去摸山体的坡度，如果摸到一个方法的坡度是向下的并且也是最陡峭的，那么就走到这个手摸到的位置，就是通过这样的方法不断一步一步的走，这个人终于走到了山底。具体可以想象成右图，那个黑点就是人。

6、反向传播：

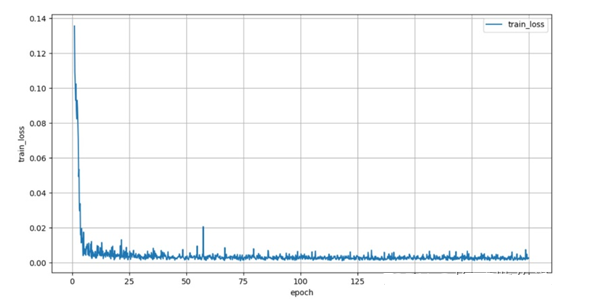
神经网络的反向传播不断更新神经网络的w和b，从而使得神经网络的输出和真实label不断的逼近，损失函数也不断的逼近0，所以我们常常将模型的训练轮次和损失值变化画图，显示出来，如果损失值在一定的轮次后趋于平缓不再下降，那么就认为模型的训练已经收敛了；

反向传播的作用，就是用来不断更新神经网络的w和b，从提高神经网络的预测准确率；

模型的训练轮次和损失值变化画图：

这篇关于全连接神经网络算法原理(激活函数、前向传播、梯度下降法、损失函数、反向传播)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---