本文主要是介绍【牛客面试必刷TOP101】Day25.BM38 在二叉树中找到两个节点的最近公共祖先和BM40 重建二叉树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者简介:大家好,我是未央;
博客首页:未央.303
系列专栏:牛客面试必刷TOP101
每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!!!
文章目录
- 前言
- 一、BM38 在二叉树中找到两个节点的最近公共祖先
- 题目描述
- 题目解析
- 二、BM40 重建二叉树
- 题目描述
- 题目解析
- 总结
前言
一、BM38 在二叉树中找到两个节点的最近公共祖先
题目描述
描述:
给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2,请找到 o1 和 o2 的最近公共祖先节点。
举例说明:
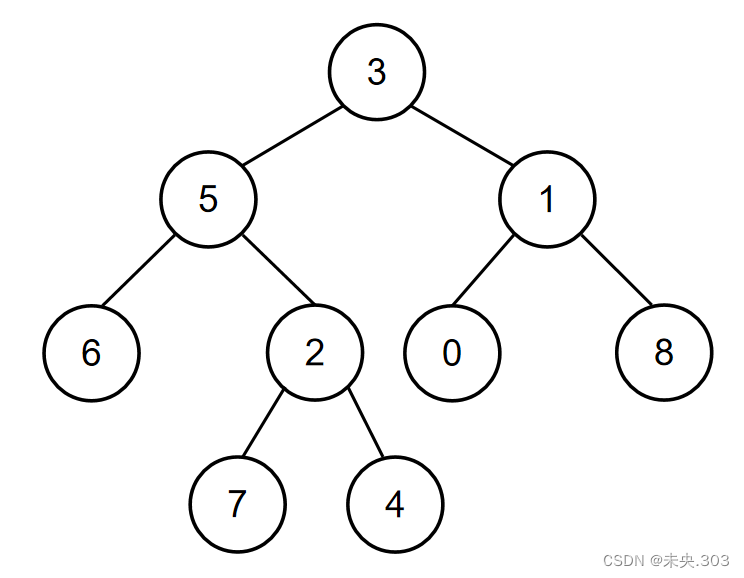
如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时,二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示:
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3,所以对应的输出为3。
节点本身可以视为自己的祖先.
示例1:
示例2:
题目解析
方法:递归
知识点:二叉树递归
二叉树的递归,则是将某个节点的左子树、右子树看成一颗完整的树,那么对于子树的访问或者操作就是对于原树的访问或者操作的子问题,因此可以自我调用函数不断进入子树。
思路:
我们也可以讨论几种情况:
- step 1:如果o1和o2中的任一个和root匹配,那么root就是最近公共祖先。
- step 2:如果都不匹配,则分别递归左、右子树。
- step 3:如果有一个节点出现在左子树,并且另一个节点出现在右子树,则root就是最近公共祖先.
- step 4:如果两个节点都出现在左子树,则说明最低公共祖先在左子树中,否则在右子树。
- step 5:继续递归左、右子树,直到遇到step1或者step3的情况。
二、BM40 重建二叉树
题目描述
描述:
给定节点数为 n 的二叉树的前序遍历和中序遍历结果,请重建出该二叉树并返回它的头结点。
举例说明:
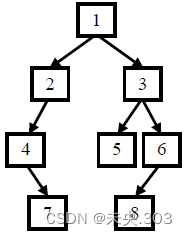
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建出如下图所示。
示例1:
示例2:
示例3:
题目解析
方法:递归
知识点:二叉树递归
二叉树的递归,则是将某个节点的左子树、右子树看成一颗完整的树,那么对于子树的访问或者操作就是对于原树的访问或者操作的子问题,因此可以自我调用函数不断进入子树。
思路:
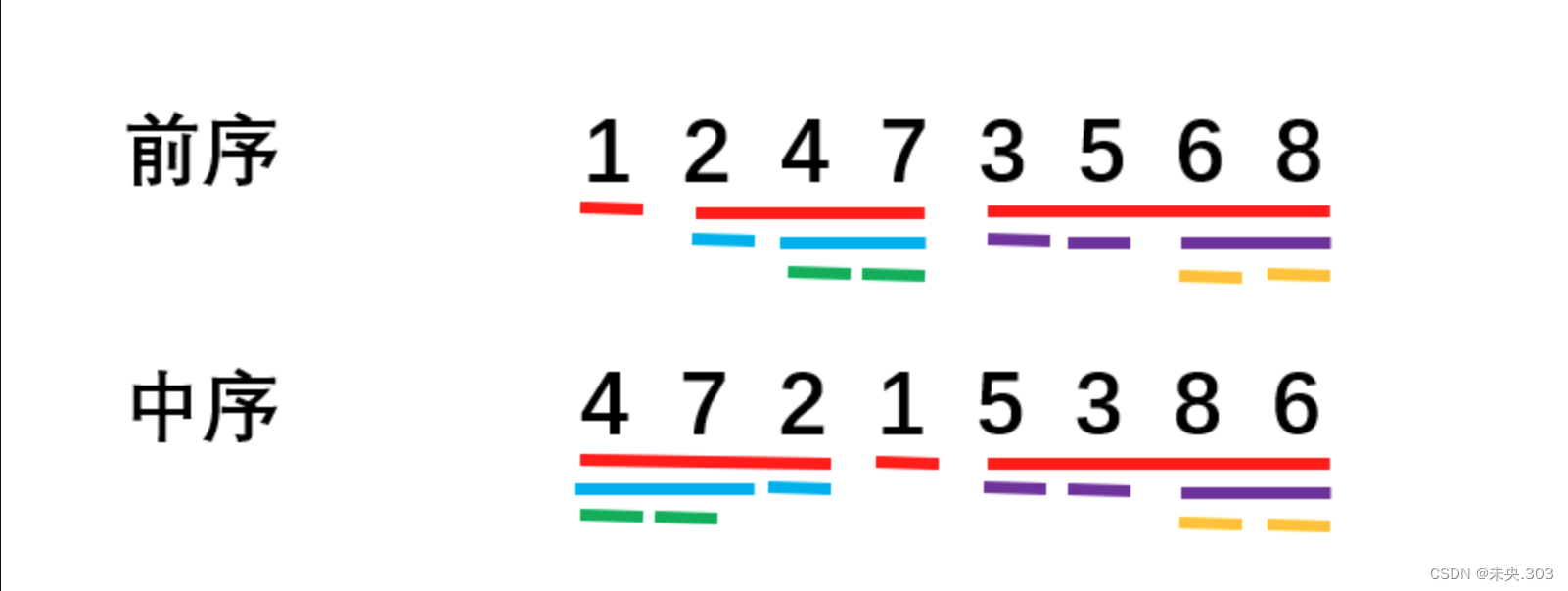
对于二叉树的前序遍历,我们知道序列的第一个元素必定是根节点的值,因为序列没有重复的元素,因此中序遍历中可以找到相同的这个元素,而我们又知道中序遍历中根节点将二叉树分成了左右子树两个部分,如下图所示:
我们可以发现,数字1是根节点,并将二叉树分成了(247)和(3568)两棵子树,而子树的的根也是相应前序序列的首位,比如左子树的根是数字2,右子树的根是数字3,这样我们就可以利用前序遍历序列找子树的根节点,利用中序遍历序列区分每个子树的节点数。
具体做法:
- step 1:先根据前序遍历第一个点建立根节点。
- step 2:然后遍历中序遍历找到根节点在数组中的位置。
- step 3:再按照子树的节点数将两个遍历的序列分割成子数组,将子数组送入函数建立子树。
- step 4:直到子树的序列长度为0,结束递归。
总结
这篇关于【牛客面试必刷TOP101】Day25.BM38 在二叉树中找到两个节点的最近公共祖先和BM40 重建二叉树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!