本文主要是介绍高维中介数据:基于贝叶斯推断的因果中介效应估计方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
摘要
该博客介绍一种基于贝叶斯推断的高维因果中介效应估计方法,适用于omics研究中的大量潜在中介变量分析。在贝叶斯框架下,利用连续收缩先验扩展了传统的因果中介分析技术,以处理高维数据。这种方法提高了全局中介分析的统计功效,并能有效地识别对路径中介效应有贡献的非零中介变量。此外,它有助于理解无活性中介变量的复合零情况结构
所需的识别假设
无测量混淆(unmeasured confounding)是指在分析因果效应时,假设没有未被观测到的变量能够同时影响暴露因素(例如,某种治疗或干预)和结果变量,从而导致估计的效应偏倚。在这个上下文中,假设(3) 表示对于暴露因素对所有中介变量的影响,不存在未测量的混淆变量。换句话说,没有未知的第三变量既影响暴露又影响中介变量。
时间顺序假设(temporal ordering assumption)是因果推理的基础,它要求暴露发生在中介变量之前,而中介变量又发生在结果之前。这确保了因果关系的方向性,即暴露导致中介变量的变化,接着中介变量的变化影响结果。在上述内容中,这一假设确保了暴露先于中介变量,中介变量再先于结果的发生,避免了反向因果关系或同时发生的误导。
条件模型,用于估计直接效应和间接效应
第一个模型是用于描述中介变量Y与暴露变量X以及可能的协变量Z之间的关系来估计平均自然直接效应
第二个模型是用于描述中介变量Y与暴露变量X在控制了其他变量(可能包括中介变量本身)情况下的关系来估计平均自然间接效应
全局间接效应的度量
全局间接效应的度量指的是通过整个高维中介变量集合的间接效应。在文中,作者提出了一种贝叶斯中介分析方法来描述这种效应,特别是在存在大量潜在中介变量,但可能只有少数真正起作用的情况下。通过在活跃系数上施加稀疏诱导先验,假设只有少量中介变量在暴露对结果的影响中起到媒介作用。这种方法允许扩展以前针对单个中介变量的分析方法,同时处理大量可能相关的中介变量,并估计它们的整体间接效应。
少量活跃的中介变量
在高维中介分析中,研究者假设只有少量的中介变量在整体集合中具有非零的间接效应,即它们对暴露-结果关系有实际的中介作用。为了识别这些活跃的中介变量,采用了一种基于贝叶斯的变量选择方法。这种方法利用了稀疏诱导先验(sparsity-inducing priors),这意味着只有少数中介变量的系数是非零的。通过这种方式,可以将识别活跃中介变量的问题转化为一个变量选择问题,并应用具有连续收缩先验的贝叶斯方法。
稀疏诱导先验
"稀疏诱导先验"(Bayesian sparse models)是一种统计建模方法,特别是在高维数据设置中,用于识别和估计那些对模型有显著影响的变量,同时处理或忽略大量可能不重要的变量。在因果中介分析的背景下,这种方法被用来通过连续收缩先验扩展之前的分析技术,以处理高维中介变量的情况。这样可以提高全球中介分析的效能,并帮助识别路径中对中介效应有真正非零贡献的变量。
贝叶斯稀疏线性混合模型(BSLMM)
贝叶斯稀疏线性混合模型(BSLMM)是一种统计模型,用于高维度中介分析。在基因组学关联研究中,这种模型被证明在检测相关协变量时具有更好的功效。BSLMM基于合理的稀疏假设,认为只有少量的中介变量在暴露与结果的关系中起作用。它同时假设所有潜在中介变量对暴露到结果的影响贡献了小但非零的效果,这与多基因和全基因模型的主要思想相一致。此外,BSLMM还假设存在一小部分中介变量具有额外或大的效果,这些被称为活跃中介变量,与全基因模型中的核心基因概念相对应。
BSLMM采用连续收缩先验,对效果进行连续性压缩,从而能够从数据中学习到潜在的中介结构,并在各种场景下表现出良好的性能。模型假设类似于连续收缩先验中的准稀疏概念。具体来说,对于第j个中介变量,预先假设其效果服从双正态分布的混合成分,即(θ_j) ∼ N(0, σ_j^2),其中σ_j^2有逆伽马先验。
该模型使用超参数来表示模型中的方差,如variances的超参数使用标准共轭先验,如inverse-gamma分布。通过设置这些超参数,可以编码关于系数稀疏性的先验信息。BSLMM通过贝叶斯推断方法自然地传播参数函数的不确定性,而不需要借助delta方法或两步法。
实现过程
library(bama)# 获取结局
Y <- bama.data$y
str(Y)
# 获取暴露
A <- bama.data$a
str(A)# 获取中介
M <- as.matrix(bama.data[, paste0("m", 1:100)], nrow(bama.data))
str(M)# 只包含截距项,没有协变量
C1 <- matrix(1, 1000, 1) C2 <- matrix(1, 1000, 1) # 初始化 beta.m 和 alpha.a 向量
beta.m <- rep(0, 100)
alpha.a <- rep(0, 100)# 设置随机种子
set.seed(12345) # 进行 fdr.bama 模型拟合
out <- fdr.bama(Y, A, M, C1, C2, beta.m, alpha.a, burnin = 100, ndraws = 120, npermutations = 10)
summary(out)# 使用 BSLMM 方法进行建模
out1 <- bama(Y = Y, A = A, M = M, C1 = C1, C2 = C2, method = "BSLMM", seed = 1234, burnin = 100, ndraws = 110, weights = NULL, inits = NULL, control = list(k = 2, lm0 = 1e-04, lm1 = 1, lma1 = 1, l = 1))
summary(out1)# 使用 PTG 方法进行建模
ptgmod = bama(Y = Y, A = A, M = M, C1 = C1, C2 = C2, method = "PTG", seed = 1234, burnin = 100, ndraws = 110, weights = NULL, inits = NULL, control = list(lambda0 = 0.04, lambda1 = 0.2, lambda2 = 0.2))# 输出相关指标的均值
mean(ptgmod$beta.a)
apply(ptgmod$beta.m, 2, mean)
apply(ptgmod$alpha.a, 2, mean)
apply(ptgmod$betam_member, 2, mean)
apply(ptgmod$alphaa_member, 2, mean)软件包介绍
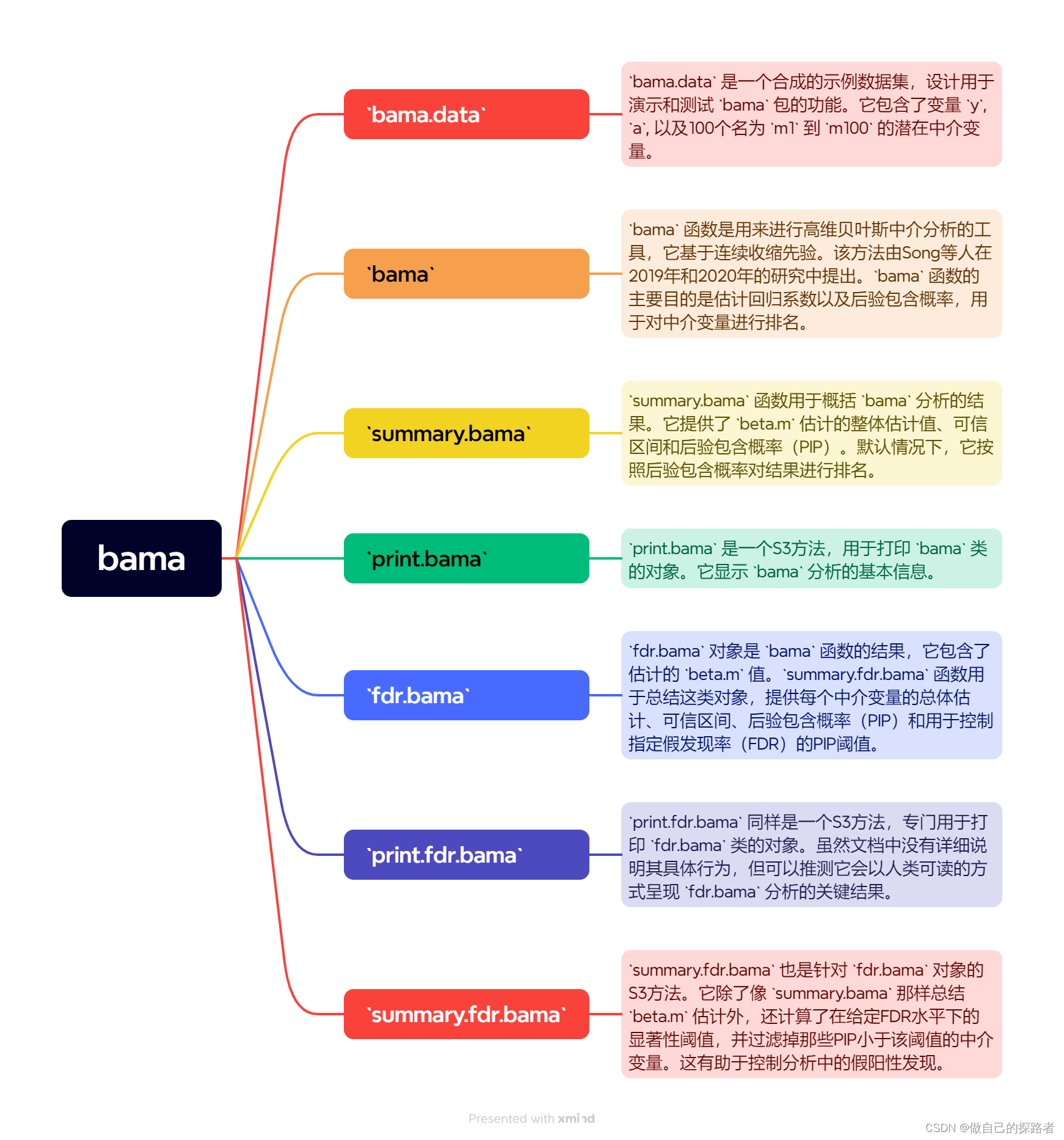
博主实操过程中总结的易错点:
C1、C2、beta.m、alpha.a的 定义与data、M维度的关系
C1 <- matrix(1, nrow(data), 1) C2 <- matrix(1, nrow(data), 1) beta.m <- rep(0, ncol(M))alpha.a <- rep(0, ncol(M))样本量大【大概超过4000的样本量】,容易出现以下错误
*** caught segfault ***
address 0x55bfdf7d6000, cause 'memory not mapped'Traceback:1: run_bama_mcmc(Y[sample(n)], A, M, C1, C2, beta.m, alpha.a, burnin, ndraws, k, lm0, lm1, lma1, l)2: FUN(X[[i]], ...)3: lapply(X = X, FUN = FUN, ...)4: sapply(seq(npermutations), permute.bama)5: fdr.bama(Y, A, M, C1, C2, beta.m, alpha.a, burnin = 100, ndraws = 200, npermutations = 10)Possible actions:
1: abort (with core dump, if enabled)
2: normal R exit
3: exit R without saving workspace
4: exit R saving workspace
Selection:npermutations 的默认值为200
`npermutations` 参数用于指定在估计零假设分布时生成的置换数量,默认值为200。这个参数在进行假发现率(FDR)控制的过程中很重要,因为它影响了对显著性阈值的估计。通过多次置换,可以构建零假设下的效应分布,进而计算出每个中介变量的显著性水平。
如果您看到这个,有钱的捧个钱场,没钱的捧个"赞"场。感谢支持!!
这篇关于高维中介数据:基于贝叶斯推断的因果中介效应估计方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




