sklearn初探（五）：自行实现朴素贝叶斯

本文主要是介绍sklearn初探（五）：自行实现朴素贝叶斯，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

sklearn初探（五）：自行实现朴素贝叶斯

前言

严格上说，这个与sklearn关系不大，不过既然都是预测问题，归于这个系列也无伤大雅。这次我实现一个朴素贝叶斯学习算法（上一篇文章中的贝叶斯是高斯分布的，与这个有点区别）。数据集链接及完整源代码在文末给出。

概述

朴素贝叶斯方法是基于贝叶斯定理的一组有监督学习算法，即“简单”地假设每对特征之间相互独立。给定一个类别 $y$ 和一个从 $x_1$ 到 $x_n$ 的相关的特征向量，贝叶斯定理阐述了以下关系:
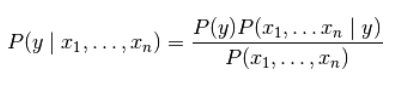
在这里插入图片描述
使用简单(naive)的假设-每对特征之间都相互独立:

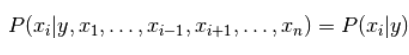
对于所有的 :i 都成立，这个关系式可以简化为

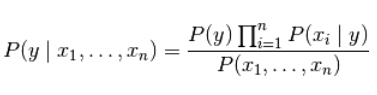
由于在给定的输入中 $P(x_1,...,x_n)$ 是一个常量，我们使用下面的分类规则:

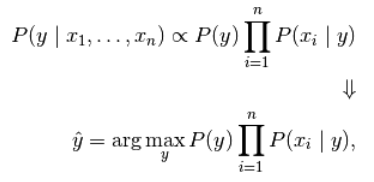
我们可以使用最大后验概率(Maximum A Posteriori, MAP) 来估计 $P (y)$ 和 $P(x_i|y)$ ; 前者是训练集中类别 $y$ 的相对频率。
各种各样的的朴素贝叶斯分类器的差异大部分来自于处理 $P(x_i|y)$ 分布时的所做的假设不同。
尽管其假设过于简单，在很多实际情况下，朴素贝叶斯工作得很好，特别是文档分类和垃圾邮件过滤。这些工作都要求一个小的训练集来估计必需参数。(至于为什么朴素贝叶斯表现得好的理论原因和它适用于哪些类型的数据，请参见下面的参考。)
相比于其他更复杂的方法，朴素贝叶斯学习器和分类器非常快。分类条件分布的解耦意味着可以独立单独地把每个特征视为一维分布来估计。这样反过来有助于缓解维度灾难带来的问题。
另一方面，尽管朴素贝叶斯被认为是一种相当不错的分类器，但却不是好的估计器(estimator)，所以不能太过于重视从 predict_proba 输出的概率。

参考资料:

H. Zhang (2004). The optimality of Naive Bayes. Proc. FLAIRS.

思路

将正例与反例各平均分为十份，然后每次各取九份为训练集，剩下的为测试集。

数据分割

还是用pandas

bank_data = pd.read_csv("../datas/train_set.csv")
marital_set = list(bank_data['marital'])
education_set = list(bank_data['education'])
default_set = list(bank_data['default'])
housing_set = list(bank_data['housing'])
y_set = list(bank_data['y'])
data_set = []

为了后续处理方便，这里将dataframe类型全部转为list

生成测试集与训练集

# divide the data set
train_set = []
test_set = []
base1 = int(i*(yes_count/10))
base2 = int((i+1)*(yes_count/10))
base3 = yes_count + int(i*(no_count/10))
base4 = yes_count + int((i+1)*(no_count/10))
for j in range(0, base1):train_set.append(data_set[j])
for j in range(base1, base2):test_set.append(data_set[j])
if base2 < yes_count:for j in range(base2, yes_count):train_set.append(data_set[j])
for j in range(yes_count, base3):train_set.append(data_set[j])
for j in range(base3, base4):test_set.append(data_set[j])
if base4 < yes_count+no_count:for j in range(base4, yes_count+no_count):train_set.append(data_set[j])

朴素贝叶斯概率计算并统计命中数

for k in test_set:yes_mar = 0yes_edu = 0yes_def = 0yes_hsg = 0no_mar = 0no_edu = 0no_def = 0no_hsg = 0for t in train_set:if t[-1] == 0:  # noif t[0] == k[0]:no_mar += 1if t[1] == k[1]:no_edu += 1if t[2] == k[2]:no_def += 1if t[3] == k[3]:no_hsg += 1else:  # yesif t[0] == k[0]:yes_mar += 1if t[1] == k[1]:yes_edu += 1if t[2] == k[2]:yes_def += 1if t[3] == k[3]:yes_hsg += 1p_yes = yes_mar/tmp_yes_count*yes_edu/tmp_yes_count*yes_def/tmp_yes_count*yes_hsg/tmp_yes_count*P_yes# print(p_yes)p_no = no_mar/tmp_no_count*no_edu/tmp_no_count*no_def/tmp_no_count*no_hsg/tmp_no_count*P_no# print(p_no)if p_yes > p_no:if k[-1] == 1:predict += 1else:if k[-1] == 0:predict += 1

评分

# print(predict)
score = predict/test_len
print(score)
with open("../output/scoresOfMyBayes.txt", "a") as sob:sob.write("The score of test "+str(i)+" is "+str(score)+'\n')

最后得分高的吓人，有八次命中率100%，看来喂数据很重要。

源代码

import pandas as pdbank_data = pd.read_csv("../datas/train_set.csv")
marital_set = list(bank_data['marital'])
education_set = list(bank_data['education'])
default_set = list(bank_data['default'])
housing_set = list(bank_data['housing'])
y_set = list(bank_data['y'])
data_set = []
for i in range(0, len(marital_set)):tmp = [marital_set[i], education_set[i], default_set[i], housing_set[i], y_set[i]]data_set.append(tmp)
label_set = bank_data['y']
label_set = list(label_set)
yes_count = 0
for i in label_set:if i == 1:yes_count += 1
no_count = len(marital_set)-yes_count
# 10-means cross validate
for i in range(0, 10):# divide the data settrain_set = []test_set = []base1 = int(i*(yes_count/10))base2 = int((i+1)*(yes_count/10))base3 = yes_count + int(i*(no_count/10))base4 = yes_count + int((i+1)*(no_count/10))for j in range(0, base1):train_set.append(data_set[j])for j in range(base1, base2):test_set.append(data_set[j])if base2 < yes_count:for j in range(base2, yes_count):train_set.append(data_set[j])for j in range(yes_count, base3):train_set.append(data_set[j])for j in range(base3, base4):test_set.append(data_set[j])if base4 < yes_count+no_count:for j in range(base4, yes_count+no_count):train_set.append(data_set[j])# calculate beginstrain_len = len(train_set)test_len = len(test_set)print(test_len)print(test_set)print(train_set)tmp_no_count = 0tmp_yes_count = 0for j in train_set:if j[-1] == 0:tmp_no_count += 1else:tmp_yes_count += 1P_yes = tmp_yes_count/train_lenP_no = tmp_no_count/train_lenpredict = 0for k in test_set:yes_mar = 0yes_edu = 0yes_def = 0yes_hsg = 0no_mar = 0no_edu = 0no_def = 0no_hsg = 0for t in train_set:if t[-1] == 0:  # noif t[0] == k[0]:no_mar += 1if t[1] == k[1]:no_edu += 1if t[2] == k[2]:no_def += 1if t[3] == k[3]:no_hsg += 1else:  # yesif t[0] == k[0]:yes_mar += 1if t[1] == k[1]:yes_edu += 1if t[2] == k[2]:yes_def += 1if t[3] == k[3]:yes_hsg += 1p_yes = yes_mar/tmp_yes_count*yes_edu/tmp_yes_count*yes_def/tmp_yes_count*yes_hsg/tmp_yes_count*P_yes# print(p_yes)p_no = no_mar/tmp_no_count*no_edu/tmp_no_count*no_def/tmp_no_count*no_hsg/tmp_no_count*P_no# print(p_no)if p_yes > p_no:if k[-1] == 1:predict += 1else:if k[-1] == 0:predict += 1# print(predict)score = predict/test_lenprint(score)with open("../output/scoresOfMyBayes.txt", "a") as sob:sob.write("The score of test "+str(i)+" is "+str(score)+'\n')