贝叶斯定理与条件独立假设：朴素贝叶斯分类方法深度解读

本文主要是介绍贝叶斯定理与条件独立假设：朴素贝叶斯分类方法深度解读，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

今天给大家分享的是朴素贝叶斯算法，这个算法在实际使用中不是很多，因为现在很多算法已经发展的很好，性能上也比朴素贝叶斯算法的好很多，因此在实际中我们其实看到在实际应用中朴素贝叶斯算法的使用已经比较少，即使出现，最终的效果也是不及其他算法的，但是作为简单、基础的算法之一，我们掌握该算法的原理还是非常有必要的，同时在实际论文研究中也经常会使用贝叶斯算法的改进版，所以大家可以多了解了解。

朴素贝叶斯算法是基于贝叶斯定理与特征条件独立假设的分类方法。基本的思路就是给定训练数据集，首先基于特征条件独立假设学习输入输出的联合概率分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。在介绍朴素贝叶斯算法之前，我们先做一些基础知识的铺垫——贝叶斯定理，该定理汇总比较重要的两个数学公式就是先验概率分布和条件概率分布，先验概率分布公式如下：

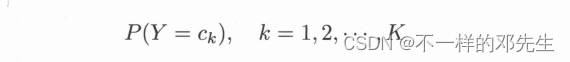
条件概率分布如下：

大家可以从公式中可以看出，先验概率分布其实就是训练数据中的不同类别数据占总体数据的比例（在实际中，频率近似概率），条件概率分布就是指在确定数据是某个类别的条件下，样本集X为指定值的概率，条件概率分布中的参数是非常多的，不仅涉及类别，还涉及特征以及特征的不同取值，假设 $X^{j}$ 表示第j个特征，该特征可能的取值有 $S_{j}$ ,j=1,2.....n,Y表示可取的类别，这样的类别有K个，那么参数个数为 $K\prod_{j=1}^{n}S_{j}$ ，因此在实际中是不可取的。从而产生了朴素贝叶斯算法中对条件概率分布做出的条件独立性假设，如果大家对独立性理解不了的话，请上网搜索答案，条件独立性假设如下：

大家可以将该公式和没有独立的公式进行对比，可以发现，独立之后的结果就是可特征进行了拆分，条件独立假设等于是说分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯算法变得简单，但是会损失一定的分类准确率。

根据训练数据，模型学习到了先验分布和条件独立概率分布，从而可以根据输入的X计算得出后验概率分布 $P(Y=c_{k}|X=x)$ ,该公式表示在知道特征X的情况下，类别为 $c_{k}$ 的概率，因此我们将该结果最大的类输出即可。后验概率公式为：

再结合特征条件独立性假设，公式变换为：

综上，朴素贝叶斯分类器可以表示为：

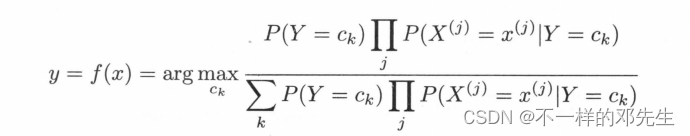
该公式表示我们将数据特征X使用朴素贝叶斯算法公式计算了在不同类别上的后验概率，最终选择这些概率中最大的一个概率，将其对应的类别输出，即判定为特征X对应的类别，在该公式中由于分母都是相同的，分母为什么是相同的，大家可以去网上查看简化版的好理解，实际在计算不同类别的时候，大家分母上的计算都是使用了所有的类别和所有的特征进行计算，因此在分母结果都是一样，从而该公式可以简化为：

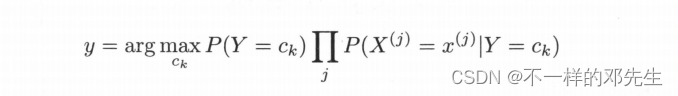
大家可能会比较好奇，为什么这里需要使用后验概率最大化来选择类结果，后验概率最大化代表类什么实际含义以及这个选择是怎么来的？大家如果学习过其他算法其实都了解，每一种算法都会有一个目标函数，朴素贝叶斯算法也不例外，假设存在一个0-1损失函数，表达式为：

期望风险函数为：

取条件期望得：

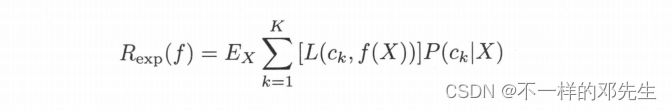
我们的目标就是追求期望损失最小话，从而可得 :

我相信大家对这几个等式应该还是比较好理解，可能稍微有难度就是第二等式，为什么直接将损失函数转换为类别不等的条件概率，是因为在上一个式子损失函数中，只有类别不等的时候我们才会存在损失函数同时损失函数为1，因此，我们下面直接转换成在确定样本X的条件下，类别不等的概率，最终的结果就转换成我们前面说的后验概率最大化，从而我们后验概率最大化是为了追求我们期望损失最小化得出来的。

朴素贝叶斯算法的总结如下：

我先使用简单直观的理解给大家讲解一下朴素贝叶斯算法的流程，后续将会使用一个实际案例给大家展示，我们首先计算先验概率，即不同类别在总数据中所占比例，接着，计算条件独立概率分布，即在不同类别下，不同特征取某个特征值的概率，遍历所有类别、所有特征以及所有特征取值，最后新的输入数据，计算其所有特征后验概率，将最大后验概率最大的类别作为该数据的类别。

fbs	restecg	output
1	0	1
0	1	1
0	0	0
0	1	0

以上是给出的训练数据，前两列代表特征，最后一列代表分类，我们将会给出测试集数据（1，1）作为案例用于算法测试，算法运行结果如下：

从计算数据可以看出，最终的结果判定为1类别。在这个实际计算过程中，大家看到了以上我们使用极大似然估计得出的概率可能为0，为了处理这种情况，于是对朴素贝叶斯算法进行了改进，得到了贝叶斯估计，条件概率的贝叶斯估计概率公式为：

和朴素贝叶斯算法相比就是在分子分母上加上了一个正数 $\lambda$ >=0,确保了计算出的概率不会等于0，当 $\lambda$ ==0时就是朴素贝叶斯使用的极大似然估计，当 $\lambda$ ==1时就是拉普拉斯平滑，贝叶斯估计的先验分布为：

大家也可以根据贝叶斯定理的前验分布和条件概率分布求出某个数据特征的后验概率，从而可以得出数据的类别，大家可以指定 $\lambda$ ==1，即拉普拉斯平滑系数计算一下上面的案例，这里我就不再计算结果了，以上就是贝叶斯算法相关全部内容，大家如果对其他内容感兴趣，关注公众号“明天科技屋”，更多精彩内容为您推荐！！！

这篇关于贝叶斯定理与条件独立假设：朴素贝叶斯分类方法深度解读的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！