Java玩转《啊哈算法》暴力枚举之坑爹奥数

2024-02-29 22:44
文章标签 java 算法 玩转 枚举 暴力 啊哈 之坑 奥数

本文主要是介绍Java玩转《啊哈算法》暴力枚举之坑爹奥数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

每个笨蛋都会随时准备杀了自己，这是最怯懦，也是最简单的出路。

路

  • 缘起
  • 代码地址
  • 枚举
    • 题1
    • 题2
    • 题2 - Plus
    • 完整代码

缘起

各位小伙伴们好呀！本人最近看了下《啊哈算法》，写的确实不错。

但稍显遗憾的是，书籍示例代码是c语言，而不是本人常用的Java。

那就弥补遗憾，说干就干，把这本书的示例语言用java写一遍， 顺带附上一些自己的理解！

今天这篇博客讲的是如何用枚举来解一些奥数题。
在这里插入图片描述

来不及买纸质书但又想尽快感受算法魅力的童鞋也甭担心，电子版的下载链接已经放到下方了，可尽情下载。

链接：https://pan.baidu.com/s/1imxiElcCorw2F-HJEnB-PA?pwd=jmgs
提取码：jmgs

代码地址

本文代码已开源：

git clone https://gitee.com/guqueyue/my-blog-demo.git

请切换到gitee分支，

然后查看aHaAlgorithm模块下的src/main/java/com/guqueyue/aHaAlgorithm/chapter_3_Enum即可！

枚举

按照惯例，首先我们来介绍一下枚举的概念：

枚举，又称穷举，说白了就是利用计算机的性能优势，暴力的穷尽每一种可能性，最后找到符合条件的情况。

在这里插入图片描述

这种思想很普遍、常用，反正遍历就对了！

下面，我们用三个奥数题，来揭开枚举的奥秘。

题1

小哼在数学课上遇到一道奥数题是这样的，口3x6528=30x8256,在两个口内填入相同的数字使得等式成立。

这一题很简单，直接遍历1-9这9个数字，看等式是否成立即可，轻松拿下：

   /*** @Description ：[]3 x 6528 = 3[] x 8256, 再两个[]内填入相同的数字使得等式成立* @Param []* @return void**/private static void test1() {for (int i = 1; i <= 9; i++) {if ((i * 10 + 3) * 6528 == (30 + i) * 8256) {System.out.println(i + "3 x 6528 = 3"+ i +" x 8256");}}}

运行得(完整代码已开源，或者在后面查看)：
在这里插入图片描述

题2

现在小哼又遇到一个稍微复杂一点的奥数题， 000+000-000,将数字1~9分别填入9个口中，每个数字只能使用一次使得等式成 立。例如173+286= 459就是一个合理的组合，请问一共有多少种合理的组合呢?注意: 173+286= 459 与286+173= 459是同一种组合 !

在这里插入图片描述
那么，这个题怎么做呢？

我们直接声明9个变量分别表示每个数，然后再采用9个for循环来暴力穷举每种情况，看看是否符合条件，并统计：

	/*** @Description ：[][][] + [][][] = [][][], 分别填入 1-9，有多少种填法？*                a b c    d e f    g h i* @Param []* @return void**/private static void test2() {int a, b, c, d, e, f, g, h, i, total = 0;for (a = 1; a <= 9; a++) {for (b = 1; b <= 9; b++) {for (c = 1; c <= 9; c++) {for (d = 1; d <= 9; d++) {for (e = 1; e <= 9; e++) {for (f = 1; f <= 9; f++) {for (g = 1; g <= 9; g++) {for (h = 1; h <= 9; h++) {for (i = 1; i <= 9; i++) {if (a != b && a != c && a != d && a != e && a != f && a != g && a != h && a != i&& b != c && b != d && b != e && b != f && b != g && b != h && b != i&& c != d && c != e && c != f && c != g && c != h && c != i&& d != e && d != f && d != g && d != h && d != i&& e != f && e != g && e != h && e != i&& f != g && f != h && f != i&& g != h && g != i&& h != i&& a * 100 + b * 10 + c + d * 100 + e * 10 + f == g * 100 + h * 10 + i) {System.out.println("" + a + b + c + " + " + d + e + f + " = " + g + h + i);total++;}}}}}}}}}}System.out.println("情况为（种）：" + total/2);}

运行得(完整代码已开源，或者在后面查看)：

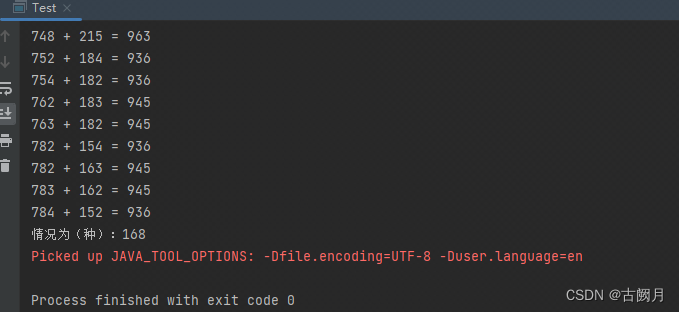
在这里插入图片描述

题2 - Plus

看了上文的代码，估计大家会觉得很恐怖，毕竟我打都打了半天。
如果要用一句歇后语来形容，那就是：封建社会老太太的裹脚布 —— 又臭又长。

在这里插入图片描述

上文的代码主要有两个问题：

  1. 声明变量太多容易让人搞错。
  2. 确定每个数互不相等的逻辑太过于冗长，简直让人崩溃。

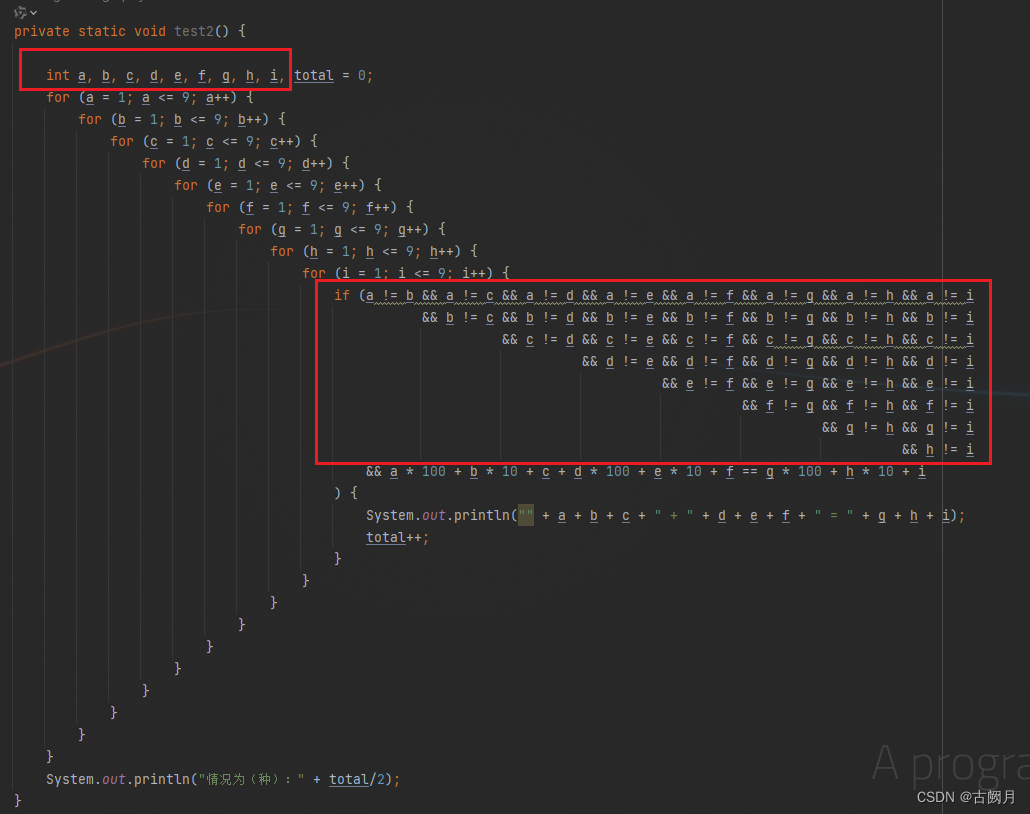
在这里插入图片描述
那么，要怎么优化呢？我这里就不卖关子了，直接给出解决方案：

  1. 变量的话可以直接声明一个数组，不同的索引位置来存放不同数，清晰明了方便。
  2. 确定每个数互不相等的部分，可以采用一个标记数组：如果有这个数，标记为1；无，则标记为0。最后，将标记数组相加，若和为9，则每个数都互不相同。

优化代码如下：

	/*** @Description ：[][][] + [][][] = [][][], 分别填入 1-9，有多少种填法？*                a b c    d e f    g h i* @Param []* @return void**/private static void test2Plus() {int[] a = new int[9]; // 用于存储int[] book = new int[10]; // 用于标记数字int total = 0;for (a[0] = 1; a[0] <= 9; a[0]++) {for (a[1] = 1; a[1] <= 9; a[1]++) {for (a[2] = 1; a[2] <= 9; a[2]++) {for (a[3] = 1; a[3] <= 9; a[3]++) {for (a[4] = 1; a[4] <= 9; a[4]++) {for (a[5] = 1; a[5] <= 9; a[5]++) {for (a[6] = 1; a[6] <= 9; a[6]++) {for (a[7] = 1; a[7] <= 9; a[7]++) {for (a[8] = 1; a[8] <= 9; a[8]++) {// 初始化 book 数组for (int i = 1; i < 10; i++) {book[i] = 0;}// 标记for (int i = 0; i < 9; i++) {book[a[i]] = 1;}int sum = 0;for (int i = 1; i <= 9; i++) {sum += book[i];}if (sum == 9&& a[0] * 100 + a[1] * 10 + a[2] + a[3] * 100 + a[4] * 10 + a[5] == a[6] * 100 + a[7] * 10 + a[8]) {System.out.println("" + a[0] + a[1] + a[2] + " + " + a[3] + a[4] + a[5] + " = " + a[6] + a[7] + a[8]);total++;}}}}}}}}}}System.out.println("情况为（种）：" + total/2);}

是不是好很多呢？运行，可得(完整代码已开源，或者在后面查看)：

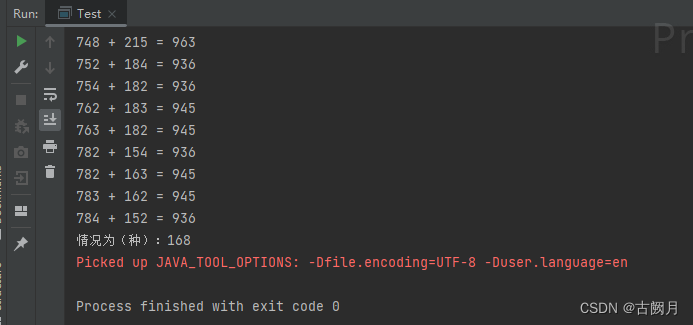
在这里插入图片描述

完整代码

package com.guqueyue.aHaAlgorithm.chapter_3_Enum;/*** @Author: guqueyue* @Description: 枚举求奥数题* @Date: 2024/1/16**/
public class Test {public static void main(String[] args) {//        test1();
//        test2();test2Plus();}/*** @Description ：[]3 x 6528 = 3[] x 8256, 再两个[]内填入相同的数字使得等式成立* @Param []* @return void**/private static void test1() {for (int i = 1; i <= 9; i++) {if ((i * 10 + 3) * 6528 == (30 + i) * 8256) {System.out.println(i + "3 x 6528 = 3"+ i +" x 8256");}}}/*** @Description ：[][][] + [][][] = [][][], 分别填入 1-9，有多少种填法？*                a b c    d e f    g h i* @Param []* @return void**/private static void test2() {int a, b, c, d, e, f, g, h, i, total = 0;for (a = 1; a <= 9; a++) {for (b = 1; b <= 9; b++) {for (c = 1; c <= 9; c++) {for (d = 1; d <= 9; d++) {for (e = 1; e <= 9; e++) {for (f = 1; f <= 9; f++) {for (g = 1; g <= 9; g++) {for (h = 1; h <= 9; h++) {for (i = 1; i <= 9; i++) {if (a != b && a != c && a != d && a != e && a != f && a != g && a != h && a != i&& b != c && b != d && b != e && b != f && b != g && b != h && b != i&& c != d && c != e && c != f && c != g && c != h && c != i&& d != e && d != f && d != g && d != h && d != i&& e != f && e != g && e != h && e != i&& f != g && f != h && f != i&& g != h && g != i&& h != i&& a * 100 + b * 10 + c + d * 100 + e * 10 + f == g * 100 + h * 10 + i) {System.out.println("" + a + b + c + " + " + d + e + f + " = " + g + h + i);total++;}}}}}}}}}}System.out.println("情况为（种）：" + total/2);}/*** @Description ：[][][] + [][][] = [][][], 分别填入 1-9，有多少种填法？*                a b c    d e f    g h i* @Param []* @return void**/private static void test2Plus() {int[] a = new int[9]; // 用于存储int[] book = new int[10]; // 用于标记数字int total = 0;for (a[0] = 1; a[0] <= 9; a[0]++) {for (a[1] = 1; a[1] <= 9; a[1]++) {for (a[2] = 1; a[2] <= 9; a[2]++) {for (a[3] = 1; a[3] <= 9; a[3]++) {for (a[4] = 1; a[4] <= 9; a[4]++) {for (a[5] = 1; a[5] <= 9; a[5]++) {for (a[6] = 1; a[6] <= 9; a[6]++) {for (a[7] = 1; a[7] <= 9; a[7]++) {for (a[8] = 1; a[8] <= 9; a[8]++) {// 初始化 book 数组for (int i = 1; i < 10; i++) {book[i] = 0;}// 标记for (int i = 0; i < 9; i++) {book[a[i]] = 1;}int sum = 0;for (int i = 1; i <= 9; i++) {sum += book[i];}if (sum == 9&& a[0] * 100 + a[1] * 10 + a[2] + a[3] * 100 + a[4] * 10 + a[5] == a[6] * 100 + a[7] * 10 + a[8]) {System.out.println("" + a[0] + a[1] + a[2] + " + " + a[3] + a[4] + a[5] + " = " + a[6] + a[7] + a[8]);total++;}}}}}}}}}}System.out.println("情况为（种）：" + total/2);}
}

这篇关于Java玩转《啊哈算法》暴力枚举之坑爹奥数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/760348。

相关文章

Java中流式并行操作parallelStream的原理和使用方法

Java中流式并行操作parallelStream的原理和使用方法

《Java中流式并行操作parallelStream的原理和使用方法》本文详细介绍了Java中的并行流（parallelStream）的原理、正确使用方法以及在实际业务中的应用案例,并指出在使用并行流... 目录Java中流式并行操作parallelStream0. 问题的产生1. 什么是parallelS
阅读更多...
Java中Redisson 的原理深度解析

Java中Redisson 的原理深度解析

《Java中Redisson的原理深度解析》Redisson是一个高性能的Redis客户端,它通过将Redis数据结构映射为Java对象和分布式对象,实现了在Java应用中方便地使用Redis,本文... 目录前言一、核心设计理念二、核心架构与通信层1. 基于 Netty 的异步非阻塞通信2. 编解码器三、
阅读更多...
SpringBoot基于注解实现数据库字段回填的完整方案

SpringBoot基于注解实现数据库字段回填的完整方案

《SpringBoot基于注解实现数据库字段回填的完整方案》这篇文章主要为大家详细介绍了SpringBoot如何基于注解实现数据库字段回填的相关方法,文中的示例代码讲解详细,感兴趣的小伙伴可以了解... 目录数据库表pom.XMLRelationFieldRelationFieldMapping基础的一些代
阅读更多...
一篇文章彻底搞懂macOS如何决定java环境

一篇文章彻底搞懂macOS如何决定java环境

《一篇文章彻底搞懂macOS如何决定java环境》MacOS作为一个功能强大的操作系统,为开发者提供了丰富的开发工具和框架,下面：本文主要介绍macOS如何决定java环境的相关资料,文中通过代码... 目录方法一：使用 which命令方法二：使用 Java_home工具（Apple 官方推荐）那问题来了，
阅读更多...
Java HashMap的底层实现原理深度解析

Java HashMap的底层实现原理深度解析

《JavaHashMap的底层实现原理深度解析》HashMap基于数组+链表+红黑树结构,通过哈希算法和扩容机制优化性能,负载因子与树化阈值平衡效率,是Java开发必备的高效数据结构,本文给大家介绍... 目录一、概述：HashMap的宏观结构二、核心数据结构解析1. 数组（桶数组）2. 链表节点（Node
阅读更多...
Java AOP面向切面编程的概念和实现方式

Java AOP面向切面编程的概念和实现方式

《JavaAOP面向切面编程的概念和实现方式》AOP是面向切面编程,通过动态代理将横切关注点（如日志、事务）与核心业务逻辑分离,提升代码复用性和可维护性,本文给大家介绍JavaAOP面向切面编程的概... 目录一、AOP 是什么？二、AOP 的核心概念与实现方式核心概念实现方式三、Spring AOP 的关
阅读更多...
详解SpringBoot+Ehcache使用示例

详解SpringBoot+Ehcache使用示例

《详解SpringBoot+Ehcache使用示例》本文介绍了SpringBoot中配置Ehcache、自定义get/set方式,并实际使用缓存的过程,文中通过示例代码介绍的非常详细,对大家的学习或者... 目录摘要概念内存与磁盘持久化存储：配置灵活性：编码示例引入依赖：配置ehcache.XML文件：配置
阅读更多...
Java 虚拟线程的创建与使用深度解析

Java 虚拟线程的创建与使用深度解析

《Java虚拟线程的创建与使用深度解析》虚拟线程是Java19中以预览特性形式引入,Java21起正式发布的轻量级线程,本文给大家介绍Java虚拟线程的创建与使用,感兴趣的朋友一起看看吧... 目录一、虚拟线程简介1.1 什么是虚拟线程？1.2 为什么需要虚拟线程？二、虚拟线程与平台线程对比代码对比示例：三
阅读更多...
一文解析C#中的StringSplitOptions枚举

一文解析C#中的StringSplitOptions枚举

《一文解析C#中的StringSplitOptions枚举》StringSplitOptions是C#中的一个枚举类型,用于控制string.Split()方法分割字符串时的行为,核心作用是处理分割后... 目录C#的StringSplitOptions枚举1.StringSplitOptions枚举的常用
阅读更多...
Java中的.close()举例详解

Java中的.close()举例详解

《Java中的.close()举例详解》.close()方法只适用于通过window.open()打开的弹出窗口,对于浏览器的主窗口,如果没有得到用户允许是不能关闭的,：本文主要介绍Java中的.... 目录当你遇到以下三种情况时，一定要记得使用 .close()：用法作用举例如何判断代码中的 input
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2