本文主要是介绍2024年新提出的算法|鹦鹉优化器(Parrot optimizer):算法及其在医疗问题中的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本期介绍一种基于训练后鹦鹉关键行为的高效优化方法——鹦鹉优化器(Parrot Optimizer, PO)。该成果于2024年2月发表在中科院2区top SCI期刊Computers in Biology and Medicine(IF=7.7)

1、简介
鹦鹉优化器(PO)是一种受训练有素的Pyrrhura Molinae鹦鹉观察到的关键行为启发的高效优化方法。该研究以定性分析和综合实验为特色,展示了鹦鹉优化器在处理各种优化问题时的独特特征。性能评估包括在35个函数上对所提出的PO进行基准测试,包括来自IEEE CEC 2022测试集的经典案例和问题,并将其与八种流行算法进行比较。结果生动地突出了PO在其探索性和开发性特征方面的竞争优势。此外,参数敏感性实验探索了所提出的PO在不同配置下的适应性。开发的PO在应用于工程设计问题时展示了有效性和优越性。为了进一步将评估扩展到现实世界的应用,我们将PO应用于疾病诊断和医学图像分割问题,这些问题在医学领域具有高度相关性和重要性。
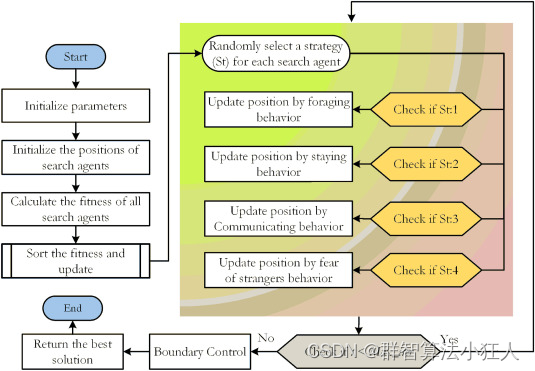
2、数学建模
2.1 种群初始化(随机)
X i 0 = l b + r a n d ( 0 , 1 ) ⋅ ( u b − l b ) X_{i}^{0}=l b+r a n d\left(0,1\right)\cdot\left(u b-l b\right) Xi0=lb+rand(0,1)⋅(ub−lb)
2.2 觅食行为
在PO的觅食行为中,它们主要通过观察食物的位置或考虑主人的位置来估计食物的大致位置,然后向各自的位置飞行。位置运动遵循以下方程:
X i t + 1 = ( X i t − X b e s t ) ⋅ L e v y ( d i m ) + r a n d ( 0 , 1 ) ⋅ ( 1 − t M a x i n v ) u M a x i n v ⋅ X m e a n t X_{i}^{t+1}=\left(X_{i}^{t}-X_{b e s t}\right)\cdot L e v y\left(d i m\right)+r a n d\left(0,1\right)\cdot\left(1-\frac{t}{M a x_{i n v}}\right)^{\frac{u}{M a x_{i n v}}}\cdot X_{m e a n}^{t} Xit+1=(Xit−Xbest)⋅Levy(dim)+rand(0,1)⋅(1−Maxinvt)Maxinvu⋅Xmeant
2.3 停留行为
Pyrrhura Molinae是一种高度社会化的生物,它的停留行为主要包括突然逃到主人身体的任何部位,在那里它保持静止一段时间。这个过程如图所示。这个过程可以表示为:
X i t + 1 = X i t + X b e s t ⋅ L e v y ( d i m ) + r a n d ( 0 , 1 ) ⋅ o n e s ( 1 , d i m ) X_{i}^{t+1}=X_{i}^{t}+X_{b e s t}\cdot L e v y(d i m)+r a n d(0,1)\cdot o n e s\left(1,d i m\right) Xit+1=Xit+Xbest⋅Levy(dim)+rand(0,1)⋅ones(1,dim)
o n e s ( 1 , d i m ) ones(1,dim) ones(1,dim)表示随机停在宿主身体某一部位的过程。

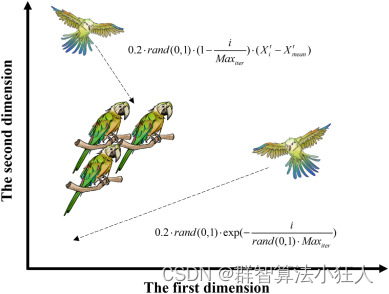
2.4 沟通行为
Pyrrhura Molinae鹦鹉是天生的群居动物,其特点是在群体内进行密切的交流。这种交流行为包括飞向羊群和不飞向羊群进行交流。在PO中,假设这两种行为发生的概率相等,并使用当前群体的平均位置来表示群体的中心。这个过程如图所示。这个过程可以表示为:
X i t + 1 = { 0.2 ⋅ r a n d ( 0 , 1 ) ⋅ ( 1 − t M a x i e r ) ⋅ ( X i t − X m e a n t ) , P ≤ 0.5 0.2 ⋅ r a n d ( 0 , 1 ) ⋅ e x p ( − t r a n d ( 0 , 1 ) ⋅ M a x i e r ) , P > 0.5 X_{i}^{t+1}=\left\{\begin{array}{c}{{0.2\cdot r a n d\left(0,1\right)\cdot\left(1-\frac t{M a x_{i e r}}\right)\cdot\left(X_{i}^{t}-X_{m e a n}^{t}\right),P\leq0.5}}\\ {{0.2\cdot r a n d\left(0,1\right)\cdot ex p\left(-\frac t{r a n d(0,1)\cdot M a x_{i e r}}\right),P\gt 0.5}}\end{array}\right. Xit+1=⎩ ⎨ ⎧0.2⋅rand(0,1)⋅(1−Maxiert)⋅(Xit−Xmeant),P≤0.50.2⋅rand(0,1)⋅exp(−rand(0,1)⋅Maxiert),P>0.5
2.5 害怕陌生人的行为
一般来说,鸟类对陌生人表现出天生的恐惧,Pyrrhura Molinae鹦鹉也不例外。它们与不熟悉的个体保持距离,并与主人一起寻求安全环境的行为如图5所示,如下所述:
X i t + 1 = X i t + r a n d ( 0 , 1 ) ⋅ c o s ( 0.5 π ⋅ t M a x i e r ) ⋅ ( X b e s t − X i t ) − c o s ( r a n d ( 0 , 1 ) ⋅ π ) ⋅ ( t M a x i e r ) 2 M a x i e r ⋅ ( X i t − X b e s t ) X_{i}^{t+1}\,=\,X_{i}^{t}\,+\,r a n d\,(0,1)\cdot c o s\,\left(0.5\pi\cdot{\frac{t}{M a x_{i e r}}}\right)\,\cdot\,\left(X_{b e s t}\,-\,X_{i}^{t}\right)-\,c o s\left(r a n d\left(0,1\right)\cdot\pi\right)\cdot\left(\frac{t}{M a x_{i e r}}\right)^{\frac{2}{M a x_{i e r}}}\,\cdot\left(X_{i}^{t}-X_{b e s t}\right) Xit+1=Xit+rand(0,1)⋅cos(0.5π⋅Maxiert)⋅(Xbest−Xit)−cos(rand(0,1)⋅π)⋅(Maxiert)Maxier2⋅(Xit−Xbest)
3.Matlab源代码下载
(1)2024年新提出的算法|鹦鹉优化器(PO)跑CEC2005数据集
(2)2024年新提出的算法|鹦鹉优化器(PO)跑CEC2017数据集
(2)2024年新提出的算法|鹦鹉优化器(PO)跑CEC2022数据集
Junbo Lian, Guohua Hui, Ling Ma, Ting Zhu, Xincan Wu, Ali Asghar Heidari, Yi Chen, Huiling Chen,Parrot optimizer: Algorithm and applications to medical problems,Computers in Biology and Medicine,2024, https://doi.org/10.1016/j.compbiomed.2024.108064.
这篇关于2024年新提出的算法|鹦鹉优化器(Parrot optimizer):算法及其在医疗问题中的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






