推荐系统 - FM模型原理和实践

本文主要是介绍推荐系统 - FM模型原理和实践，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文收录在推荐系统专栏，专栏系统化的整理推荐系统相关的算法和框架，并记录了相关实践经验，所有代码都已整理至推荐算法实战集合(hub-recsys)。

目录

一. FM概述

二. FM原理

2.1 模型推导

2.2 模型求解

三. FM实战

---

一. FM概述

FM（Factorization Machines，因子分解机），简称FM模型，由Steffen Rendle于2010年在ICDM上提出。FM模型是一种通用的预测方法，主要有以下的特点和优势，基于此在推荐系统和计算广告领域[如: CTR预估(click-through rate)]具备良好的表现。

1. 特征组合：FM实现了二阶特征交叉，无需人工也非像MLP结构是种低效率地捕获特征组合的结构。
2. 引入隐向量：极大地减少模型参数，增强模型泛化能力，稀疏数据可学习。
3. 线性复杂度：通过公式的转化，实现线性计算复杂度。

二. FM原理

2.1 模型推导

在正式引入FM之前，LR模型是CTR预估领域早期最成功的模型 —“线性模型+人工特征组合引入非线性”的模式。具有简单方便易解释容易上规模等诸多好处。

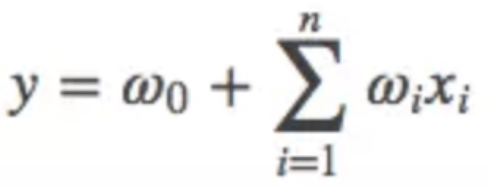
实际应用的场景中，大量的特征是关联的。然而线性模型是假设特征相互独立，并没有考虑到特征与特征之间的相互关系，LR中只能依靠人工特征交叉，效率不高，能否在模型层面引入特征组合的能力？

我们采用多项式模型，用来表述特征间的相关性，在多项式模型中，特征xi与xj的组合用xixj表示。为了简单起见，我们讨论二阶多项式模型。具体的模型表达式如上所示，n表示样本的特征数量，xi表示第i个特征。然而上述的多项式模型存在以下缺点：

• 参数规模复杂，组合部分的特征相关参数共有n(n−1)/2个。
• 由于数据稀缺，满足xi,xj都不为0的情况非常少，这样将导致ωij无法通过训练得出。

为了解决上述的多项式模型的缺点，可以对二阶项参数施加某种限制，减少模型参数的自由度。FM 施加的限制是要求二阶项系数矩阵是低秩的，能够分解为低秩矩阵的乘积：

以上就是FM模型的表达式。k是超参数，即lantent vector的维度，可以设置较少的k值（一般设置在100以内，k<<n），就将参数个数减少到 kn，极大地减少模型参数，增强模型泛化能力。然而上式如果要计算的话，时间复杂度是O(kn2), 可以通过如下方式化简。

上式为FM的最终结果，接下来我们需要对FM的模型参数求解。

 

2.2 模型求解

在获得FM的模型方程后，根据不同的应用，FM可以采用不同的损失函数loss function来作为优化目标：

• 如回归Regression：y^(x)直接作为预测值，损失函数可以采用least square error；
• 二值分类Binary Classification：y^(x)需转化为二值标签，如0,1。损失函数可以采用hinge loss或logit loss；
• 排序Rank：x可能需要转化为pair-wise的形式如(X^a,X^b)，损失函数可以采用pairwise loss。

然后对模型进行训练，目前FM的学习算法主要包括以下三种：

1. 随机梯度下降法（Stochastic Gradient Descent, SGD）
2. 交替最小二乘法（Alternating Least Square Method，ALS）
3. 马尔科夫链蒙特卡罗法（Markov Chain Monte Carlo，MCMC）

随机梯度下降的方法来求解，如下：

最终的模型求解和得带如下所示，主要超参数有：初始化参数、学习率、正则化稀疏

FM和MF的关系？

本质上，MF模型是FM模型的特例，MF可以被认为是只有User ID 和Item ID这两个特征Fields的FM模型，MF将这两类特征通过矩阵分解，来达到将这两类特征embedding化表达的目的。而FM则可以看作是MF模型的进一步拓展，除了User ID和Item ID这两类特征外，很多其它类型的特征，都可以进一步融入FM模型里，它将所有这些特征转化为embedding低维向量表达，并计算任意两个特征embedding的内积，就是特征组合的权重。

FM继承了MF的特征embedding化表达这个优点，同时引入了更多Side information作为特征，将更多特征及Side information embedding化融入FM模型中。所以很明显FM模型更灵活，能适应更多场合的应用范围。

 

三. FM实战

利用movieLen和基于随机梯度下降的方法来实现FM算法，梯度下降的关键代码如下所示。

def _sgd_theta_step(self, x_data_ptr, x_ind_ptr, xnnz, y):mult = 0.0w0 = self.w0w = self.wv = self.vgrad_w = self.grad_wgrad_v = self.grad_vlearning_rate = self.learning_ratereg_0 = self.reg_0reg_w = self.reg_wreg_v = self.reg_vp = self._predict_instance(x_data_ptr, x_ind_ptr, xnnz)if self.task == "regression":p = min(self.max_target, p)p = max(self.min_target, p)mult = 2 * (p - y);else:mult = y * ((1.0 / (1.0 + math.exp(-y * p))) - 1.0)# Update global biasif self.k0:grad_0 = multw0 -= learning_rate * (grad_0 + 2 * reg_0 * w0)# Update feature biasesif self.k1:for i in range(xnnz):feature = x_ind_ptr[i]grad_w[feature] = mult * x_data_ptr[i]w[feature] -= learning_rate * (grad_w[feature]+ 2 * reg_w * w[feature])# Update feature factor vectorsfor f in range(self.num_factors):for i in range(xnnz):feature = x_ind_ptr[i]grad_v[f, feature] = mult * (x_data_ptr[i] * (self.sum[f] - v[f, feature] * x_data_ptr[i]))v[f, feature] -= learning_rate * (grad_v[f, feature] + 2 * reg_v[f] * v[f, feature])

完整的实现代码：https://github.com/hxyue/hub-recsys

 

这篇关于推荐系统 - FM模型原理和实践的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---