左神的算法课笔记整理

简介：本文包含了 递归行为时间复杂度、快速排序的空间复杂度、堆排序、排序算法稳定性、工程中的综合排序算法、有关排序小知识

递归行为 递归行为时间复杂度

快速排序的空间复杂度

O(logN) ←原因是储存断点，二分再释放的过程，有多少个二分点，就需要多少的存储空间

堆排序

堆：完全二叉树

大根堆：任何一个子树的最大值都是这个子树的头部

插入操作：按照从左到右顺序构建大根堆，每插入一个数都与其父节点作比较，若比父节点大则交换，还比父节点大则继续交换…

若数组中某值变小：与两个孩子中最大值交换，重复此过程，一直到不必交换或者到叶节点

删除操作：先把堆顶弹出来，再把最后一个位置的数放在堆顶，再用上个算法调整

堆排序算法：大根堆堆顶与最后一个数交换，堆size--，然后heapify，堆顶继续交换……直到堆剩下最后一个数，那么就排好啦

排序算法稳定性

            桶排序、 计数排序、 基数排序的介绍

• 非基于比较的排序， 与被排序的样本的实际数据状况很有关系， 所以实际中并不经常使用
• 时间复杂度O(N)， 额外空间复杂度O(N)
• 稳定的排序

工程中的综合排序算法

• 如果数组很长，会先判断是基础类型还是你定义的class

                基础类型：快排（因为不要求稳定）

                自己定义的class：归并排序（希望稳定）

• 数组长度很短：插入排序（因为常数项很低，小样本会很快）（数组长度小于60）

有关排序小知识：

1. 归并排序的额外空间复杂度可以变成O(1)， 但是非常难， 不需要掌握， 可以搜“归并排序 内部缓存法”
2. 快速排序可以做到稳定性问题， 但是非常难， 不需要掌握，可以搜“01 stable sort”
3. 有一道题目， 是奇数放在数组左边， 偶数放在数组右边，且要求稳定，要求时间复杂O(N)，空间复杂O(1)，那么这是很难做到的，因为这属于0，1的稳定问题，相当于快排的partition过程，快排的partition可以做到时间O(N)，空间O(1)，但不是稳定的，“01 stable sort”可以做到但非常复杂。

认识哈希函数和哈希表

1. 同一个数一定映射到固定的数，不同的数可能映射到相同的数（因为是大集合映射到小集合）
2. 映射后在值域均匀分布
3. 映后的值域膜某个数也是均匀分布
4. 如何通过一个哈希函数创造无数个哈希函数？比如映射后是16位，记前8位为h1,后8位为h2，这样创造新的哈希函数：

• h1+1*h2=h3
• h1+2*h2=h41
• h1+3*h2=h5

1. 哈希值映射到同一个数怎么办？用链表。并且链表的长度也是均匀的。
2. 链太长就要扩容: 重新计算哈希值，放入新的容器（可以离线扩容）
3. 在java里：性能是O(logN)，每个桶里是个红黑树

一个应用：

给100T的大文件，每行是一个字符串，找出所有相同字符串

主动问：给几台机器？答：1000

那就输入哈希函数得到数字再模1000，那么相同的必被分到同一个机器，同一个机器可以再用哈希，并行处理。

认识布隆过滤器

应用：黑名单里有100亿个url，每个url64字节（640G），判断是否在黑名单里

相比于哈希表的完全正确，布隆过滤器有失误率。

准备m个比特位的数组（int数组m/32个值），把url输入k个哈希函数，输出k个哈希值，膜m，把映射到的位置标记为false；

验证的时候：看看这个url的k个值是否都为false

1. 数组长度取决于：url个数，预期失误率

n样本量，p预期失误率

当n=100亿，p=0.0001时，需要22.3G

1. 确定哈希函数的个数

1. 真实失误率

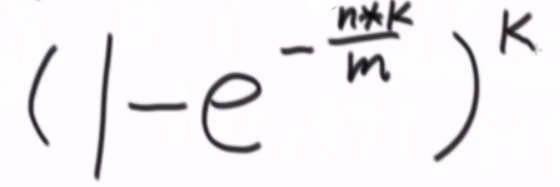
*怎么抗压：前端抗压集群，设置缓存

认识一致性哈希

一种服务器的设计

服务器迁移代价变得很低，同时负载均衡

如何让节点均匀？虚拟节点技术

将整个哈希值空间组织成一个虚拟的圆环，如假设某哈希函数H的值空间为0-2^32-1

每一个物理节点，创造1000个虚拟节点给它，比如：

M1创造出M1-1，M1-2，M1-3……M1-1000

M2创造出M2-1，M2-2，M2-3……M2-1000

M3创造出M3-1，M3-2，M3-3……M3-1000

创造这3000个节点哈希值的排序后数组arr

每加一个键值对的哈希值进去，就用二分在arr中找最近一个大于它的数，并分给这个服务器。

这样一来可以保证分给各服务器的键值对数量是均匀的。

新增物理节点（服务器）时，也创造1000个虚拟节点，并把每个虚拟节点它下一个虚拟节点的数据拿到自己这里来。此时它们又是平均分配的了

并查集结构

非常快的检查两个元素是否属于一个集合

合并两个集合时，把少的头节点挂在多的头节点下面。

优化:查找时沿途所有节点改为直接连到头节点。

（非递归版findhead）

只要保证头结点的size（集合大小）是正确的就可以了

查询次数+合并次数达到O(n), 那么单次操作时间复杂度为O(1)

应用：岛问题