【算法与数据结构】684、685、LeetCode冗余连接I II

2024-02-24 06:44
文章标签 leetcode 算法 连接 数据结构 ii 冗余 685 684

本文主要是介绍【算法与数据结构】684、685、LeetCode冗余连接I II，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

  • 一、684、冗余连接 I
  • 二、685、冗余连接 II
  • 三、完整代码

所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、684、冗余连接 I

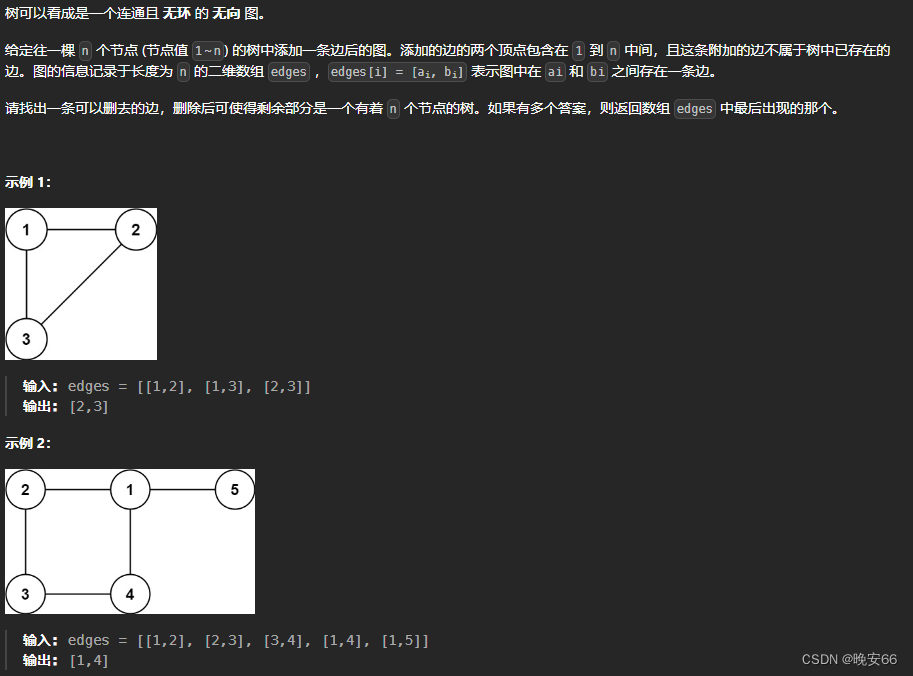
在这里插入图片描述
在这里插入图片描述

  思路分析：题目给出一个无向有环图，要求去掉一个边以后构成一个树（多叉树）。那么我们根据并查集理论，将所有的边加入到并查集中，前面的边先连上，边上的两个节点如果不在同一个集合中，就加入集合。如果两个节点已经出现在同一集合里，说明这两个节点已经连接在一起了，再加入一条后来的边就会构成环。因此去掉后来的这条边即可。

  程序如下：

class Solution {
private:int n = 200005;		// 节点数量 200000vector<int> father = vector<int>(n, 0);	// C++里面的一种数据结构// 并查集初始化void init() {for (int i = 0; i < n; ++i) {father[i] = i;}}// 并查集里寻根的过程int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);    // 路径压缩}// 判断 u 和 v是否找到同一个根bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;}// 将v->u 这条边加入并查集void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回father[v] = u;      // 根不同，则令v的父节点为u}
public:vector<int> findRedundantConnection(vector<vector<int>>& edges) {init();for (int i = 0; i < edges.size(); i++) {if (isSame(edges[i][0], edges[i][1])) return edges[i];else join(edges[i][0], edges[i][1]);}return { };}
};

复杂度分析：

  • 时间复杂度： O ( n l o g n ) O(nlogn) O(nlogn)，其中 n n n是图中边的个数，即edges数组的大小。需要遍历图中的 n n n条边，对于每条边，需要对两个节点查找祖先，如果两个节点的祖先不同则需要进行合并，需要进行2次查找和最多1次合并。一共需要进行 2 n 2n 2n次查找和最多 n n n次合并，因此总时间复杂度是 O ( 2 n log ⁡ ⁡ n ) = O ( n log ⁡ n ) O(2n \log ⁡n)=O(n \log n) O(2nlog⁡n)=O(nlogn)。
  • 空间复杂度： O ( n ) O(n) O(n)，主要开销用于father数组。

二、685、冗余连接 II

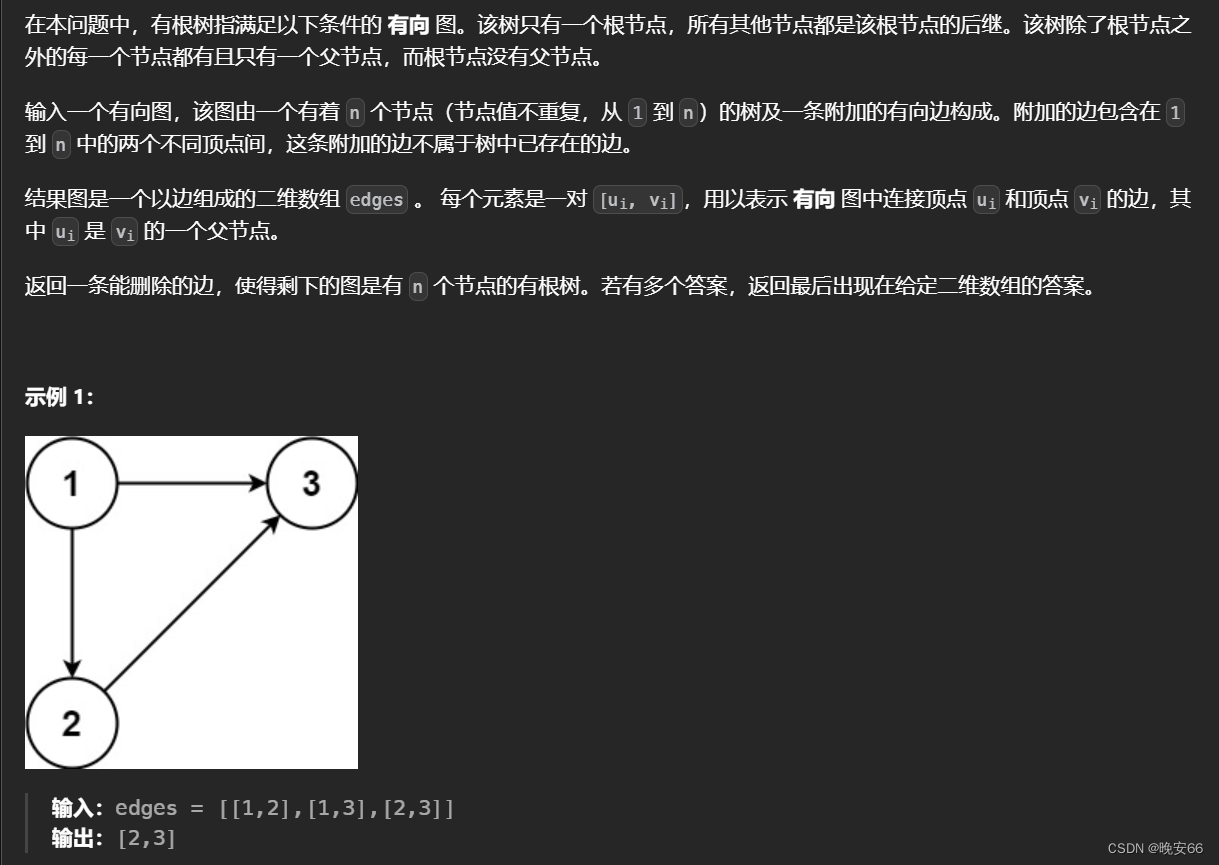
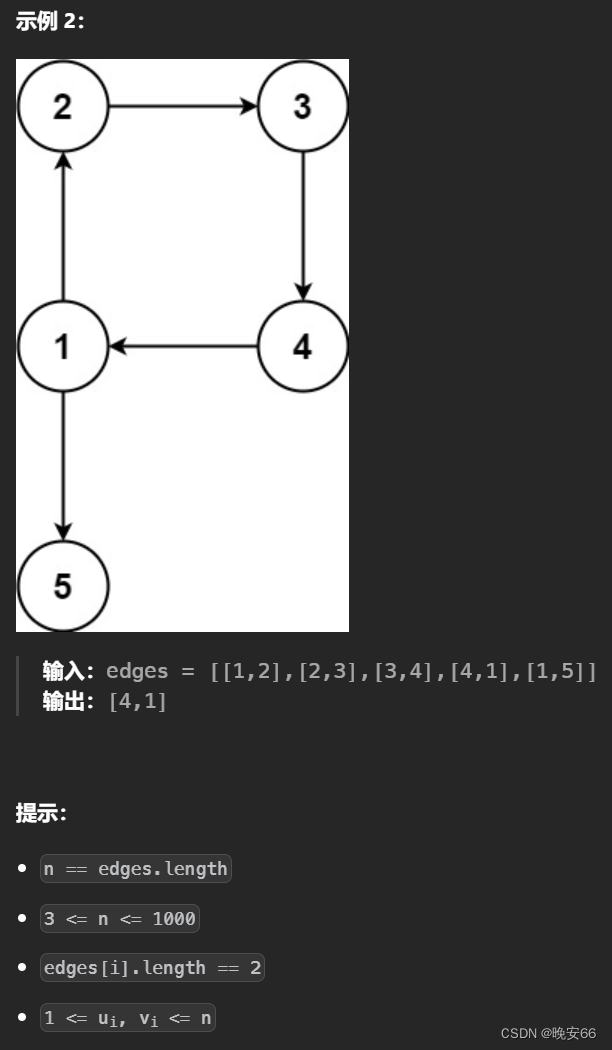
在这里插入图片描述
在这里插入图片描述

  思路分析：题目说明，图原本是一棵树，只不过在不增加节点的情况下多了一条额外的边，我们需要把多出来的这一条边去除。与684题区别在于本题是有向图，684题是无向图。关于有向图有出度和入度的说法。出度是指节点发出的箭头数量，入度是指指向节点的箭头数量。根节点没有父节点，其他节点有且只有一个父节点，那么多出来的一条边就会改变了节点的入度数量，而出度的数量无法成为判断标准（一个父节点可以由多个子节点，出度数量不唯一）。出现入度为2的节点有以下两种情况：

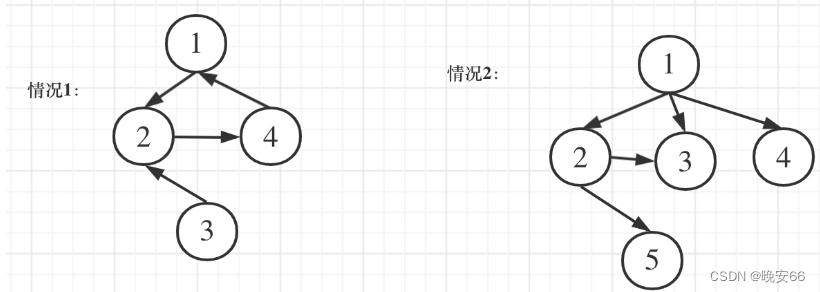
在这里插入图片描述

  如果加入的这条边形成了有向环，那么入度不会改变：
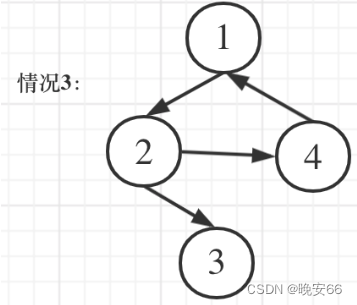
在这里插入图片描述
  统计节点入度：

int inDegree[N] = {0}; // 记录节点入度
n = edges.size(); // 边的数量
for (int i = 0; i < n; i++) {inDegree[edges[i][1]]++; // 统计入度
}

  前两种入度为2的情况一定是删除入度为2的节点的两条边其中一条。题目还要求返回最后出现在二维数组的答案，也就是说要从后往前遍历，删除以后判断剩下的图是否构成树。如果说两条边都可以构成树，就删除最后一条边。

vector<int> vec; // 记录入度为2的边（如果有的话就两条边）
// 找入度为2的节点所对应的边，注意要倒序，因为优先返回最后出现在二维数组中的答案
for (int i = n - 1; i >= 0; i--) {if (inDegree[edges[i][1]] == 2) {vec.push_back(i);}
}
// 处理图中情况1 和 情况2
// 如果有入度为2的节点，那么一定是两条边里删一个，看删哪个可以构成树
if (vec.size() > 0) {if (isTreeAfterRemoveEdge(edges, vec[0])) {return edges[vec[0]];} else {return edges[vec[1]];}
}

  情况三，明确没有入度为2的情况，一定是有环，我们从后往前遍历，找到删除以后的那个可以构成树的边。那么如何判断一个图是否为树，应该应用到并查集了。因为如果两个点所在的边在添加图之前如果就可以在并查集里找到了相同的根，那么这条边添加上之后 这个图一定不是树了。

// 情况三：在有向图里找到删除的那条边，使其变成树vector<int> getRemoveEdge(const vector<vector<int>>& edges) {init(); // 初始化并查集for (int i = 0; i < n; i++) { // 遍历所有的边if (isSame(edges[i][0], edges[i][1])) { // 构成有向环了，就是要删除的边return edges[i];}join(edges[i][0], edges[i][1]);}return {};}

  程序如下：

// 685、冗余连接II-并查集
class Solution2 {
private:static const int N = 1005;		// 节点数量 1005int father[N];int n;                          // 边的数量// 并查集初始化void init() {for (int i = 0; i < n; i++) {father[i] = i;}}// 并查集里寻根的过程int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);    // 路径压缩}// 判断 u 和 v是否找到同一个根bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;}// 将v->u 这条边加入并查集void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回father[v] = u;      // 根不同，则令v的父节点为u}// 情况三：在有向图里找到删除的那条边，使其变成树vector<int> getRemoveEdge(const vector<vector<int>>& edges) {init(); // 初始化并查集for (int i = 0; i < n; i++) { // 遍历所有的边if (isSame(edges[i][0], edges[i][1])) { // 构成有向环了，就是要删除的边return edges[i];}join(edges[i][0], edges[i][1]);}return {};}// 删一条边之后判断是不是树bool isTreeAfterRemoveEdge(const vector<vector<int>>& edges, int deleteEdge) {init(); // 初始化并查集for (int i = 0; i < n; i++) {if (i == deleteEdge) continue;if (isSame(edges[i][0], edges[i][1])) { // 构成有向环了，一定不是树return false;}join(edges[i][0], edges[i][1]);}return true;}
public:vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {int inDegree[N] = { 0 }; // 记录节点入度n = edges.size(); // 边的数量for (int i = 0; i < n; i++) {inDegree[edges[i][1]]++; // 统计入度}vector<int> vec; // 记录入度为2的边（如果有的话就两条边）// 找入度为2的节点所对应的边，注意要倒序，因为优先返回最后出现在二维数组中的答案for (int i = n - 1; i >= 0; i--) {if (inDegree[edges[i][1]] == 2) {vec.push_back(i);}}// 情况一和情况二：如果有入度为2的节点，那么一定是两条边里删一个，看删哪个可以构成树if (vec.size() > 0) {if (isTreeAfterRemoveEdge(edges, vec[0])) {return edges[vec[0]];}else {return edges[vec[1]];}}// 情况三：明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了return getRemoveEdge(edges);}
};

复杂度分析：

  • 时间复杂度： O ( n log ⁡ n ) O(n \log n) O(nlogn)。
  • 空间复杂度： O ( n ) O(n) O(n)。

三、完整代码

# include <iostream>
# include <vector>
using namespace std;// 684、冗余连接I-并查集
class Solution {
private:int n = 200005;		// 节点数量 200000vector<int> father = vector<int>(n, 0);	// C++里面的一种数据结构// 并查集初始化void init() {for (int i = 0; i < n; i++) {father[i] = i;}}// 并查集里寻根的过程int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);    // 路径压缩}// 判断 u 和 v是否找到同一个根bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;}// 将v->u 这条边加入并查集void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回father[v] = u;      // 根不同，则令v的父节点为u}
public:vector<int> findRedundantConnection(vector<vector<int>>& edges) {init();for (int i = 0; i < edges.size(); i++) {if (isSame(edges[i][0], edges[i][1])) return edges[i];else join(edges[i][0], edges[i][1]);}return { };}
};// 685、冗余连接II-并查集
class Solution2 {
private:static const int N = 1005;		// 节点数量 1005int father[N];int n;                          // 边的数量// 并查集初始化void init() {for (int i = 0; i < n; i++) {father[i] = i;}}// 并查集里寻根的过程int find(int u) {return u == father[u] ? u : father[u] = find(father[u]);    // 路径压缩}// 判断 u 和 v是否找到同一个根bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;}// 将v->u 这条边加入并查集void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回father[v] = u;      // 根不同，则令v的父节点为u}// 情况三：在有向图里找到删除的那条边，使其变成树vector<int> getRemoveEdge(const vector<vector<int>>& edges) {init(); // 初始化并查集for (int i = 0; i < n; i++) { // 遍历所有的边if (isSame(edges[i][0], edges[i][1])) { // 构成有向环了，就是要删除的边return edges[i];}join(edges[i][0], edges[i][1]);}return {};}// 删一条边之后判断是不是树bool isTreeAfterRemoveEdge(const vector<vector<int>>& edges, int deleteEdge) {init(); // 初始化并查集for (int i = 0; i < n; i++) {if (i == deleteEdge) continue;if (isSame(edges[i][0], edges[i][1])) { // 构成有向环了，一定不是树return false;}join(edges[i][0], edges[i][1]);}return true;}
public:vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {int inDegree[N] = { 0 }; // 记录节点入度n = edges.size(); // 边的数量for (int i = 0; i < n; i++) {inDegree[edges[i][1]]++; // 统计入度}vector<int> vec; // 记录入度为2的边（如果有的话就两条边）// 找入度为2的节点所对应的边，注意要倒序，因为优先返回最后出现在二维数组中的答案for (int i = n - 1; i >= 0; i--) {if (inDegree[edges[i][1]] == 2) {vec.push_back(i);}}// 情况一和情况二：如果有入度为2的节点，那么一定是两条边里删一个，看删哪个可以构成树if (vec.size() > 0) {if (isTreeAfterRemoveEdge(edges, vec[0])) {return edges[vec[0]];}else {return edges[vec[1]];}}// 情况三：明确没有入度为2的情况，那么一定有有向环，找到构成环的边返回就可以了return getRemoveEdge(edges);}
};int main() {//   // 684、冗余连接I-并查集-测试案例//vector<vector<int>> edges = { {1, 2}, {1, 3}, {2, 3} };//Solution s1;//vector<int> result = s1.findRedundantConnection(edges);// 685、冗余连接II-并查集-测试案例vector<vector<int>> edges = { {1, 2}, {1, 3}, {2, 3} };Solution2 s2;vector<int> result = s2.findRedundantDirectedConnection(edges);for (vector<int>::iterator it = result.begin(); it < result.end(); it++) {cout << *it << ' ';}cout << endl;system("pause");return 0;
}

end

这篇关于【算法与数据结构】684、685、LeetCode冗余连接I II的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/741271。

相关文章

SQL 中多表查询的常见连接方式详解

SQL 中多表查询的常见连接方式详解

《SQL中多表查询的常见连接方式详解》本文介绍SQL中多表查询的常见连接方式,包括内连接（INNERJOIN）、左连接（LEFTJOIN）、右连接（RIGHTJOIN）、全外连接（FULLOUTER... 目录一、连接类型图表（ASCII 形式）二、前置代码（创建示例表）三、连接方式代码示例1. 内连接（I
阅读更多...
Go语言中三种容器类型的数据结构详解

Go语言中三种容器类型的数据结构详解

《Go语言中三种容器类型的数据结构详解》在Go语言中,有三种主要的容器类型用于存储和操作集合数据：本文主要介绍三者的使用与区别,感兴趣的小伙伴可以跟随小编一起学习一下... 目录基本概念1. 数组（Array）2. 切片（Slice）3. 映射（Map）对比总结注意事项基本概念在 Go 语言中，有三种主要
阅读更多...
java如何通过Kerberos认证方式连接hive

java如何通过Kerberos认证方式连接hive

《java如何通过Kerberos认证方式连接hive》该文主要介绍了如何在数据源管理功能中适配不同数据源（如MySQL、PostgreSQL和Hive）,特别是如何在SpringBoot3框架下通过... 目录Java实现Kerberos认证主要方法依赖示例续期连接hive遇到的问题分析解决方式扩展思考总
阅读更多...
Python中连接不同数据库的方法总结

Python中连接不同数据库的方法总结

《Python中连接不同数据库的方法总结》在数据驱动的现代应用开发中,Python凭借其丰富的库和强大的生态系统,成为连接各种数据库的理想编程语言,下面我们就来看看如何使用Python实现连接常用的几... 目录一、连接mysql数据库二、连接PostgreSQL数据库三、连接SQLite数据库四、连接Mo
阅读更多...
oracle如何连接登陆SYS账号

oracle如何连接登陆SYS账号

《oracle如何连接登陆SYS账号》在Navicat12中连接Oracle11g的SYS用户时,如果设置了新密码但连接失败,可能是因为需要以SYSDBA或SYSOPER角色连接,解决方法是确保在连接... 目录oracle连接登陆NmOtMSYS账号工具问题解决SYS用户总结oracle连接登陆SYS账号
阅读更多...
VScode连接远程Linux服务器环境配置图文教程

VScode连接远程Linux服务器环境配置图文教程

《VScode连接远程Linux服务器环境配置图文教程》：本文主要介绍如何安装和配置VSCode,包括安装步骤、环境配置（如汉化包、远程SSH连接）、语言包安装（如C/C++插件）等,文中给出了详... 目录一、安装vscode二、环境配置1.中文汉化包2.安装remote-ssh，用于远程连接2.1安装2
阅读更多...
关于rpc长连接与短连接的思考记录

关于rpc长连接与短连接的思考记录

《关于rpc长连接与短连接的思考记录》文章总结了RPC项目中长连接和短连接的处理方式,包括RPC和HTTP的长连接与短连接的区别、TCP的保活机制、客户端与服务器的连接模式及其利弊分析,文章强调了在实... 目录rpc项目中的长连接与短连接的思考什么是rpc项目中的长连接和短连接与tcp和http的长连接短
阅读更多...
Python中的随机森林算法与实战

Python中的随机森林算法与实战

《Python中的随机森林算法与实战》本文详细介绍了随机森林算法,包括其原理、实现步骤、分类和回归案例,并讨论了其优点和缺点,通过面向对象编程实现了一个简单的随机森林模型,并应用于鸢尾花分类和波士顿房... 目录1、随机森林算法概述2、随机森林的原理3、实现步骤4、分类案例：使用随机森林预测鸢尾花品种4.1
阅读更多...
Xshell远程连接失败以及解决方案

Xshell远程连接失败以及解决方案

《Xshell远程连接失败以及解决方案》本文介绍了在Windows11家庭版和CentOS系统中解决Xshell无法连接远程服务器问题的步骤,在Windows11家庭版中,需要通过设置添加SSH功能并... 目录一.问题描述二.原因分析及解决办法2.1添加ssh功能2.2 在Windows中开启ssh服务2
阅读更多...
Redis连接失败：客户端IP不在白名单中的问题分析与解决方案

Redis连接失败：客户端IP不在白名单中的问题分析与解决方案

《Redis连接失败：客户端IP不在白名单中的问题分析与解决方案》在现代分布式系统中,Redis作为一种高性能的内存数据库,被广泛应用于缓存、消息队列、会话存储等场景,然而,在实际使用过程中,我们可能... 目录一、问题背景二、错误分析1. 错误信息解读2. 根本原因三、解决方案1. 将客户端IP添加到Re
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2