「一本通入门 2.3」踩方格（典型的递推题目，值得一看）

本文主要是介绍「一本通入门 2.3」踩方格（典型的递推题目，值得一看），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【题目描述】

有一个方格矩阵，矩阵边界在无穷远处。我们做如下假设：

a、每走一步时，只能从当前方格移动一格，走到某个相邻的方格上；

b、走过的格子立即塌陷无法再走第二次；

c、只能向北、东、西三个方向走；

请问：如果允许在方格矩阵上走n步，共有多少种不同的方案。2种走法只要有一步不一样，即被认为是不同的方案。

【输入】

允许在方格上行走的步数n(n≤20)。

【输出】

计算出的方案数量。

【输入样例】

【输出样例】

乍一看，是不是完全没有思路？没事，我们慢慢来理

错误一：方格中走到(i,j)位置的方案数等于走到方格中(i,j-1),(i,j+1),(i-1,j)的方案数之和。

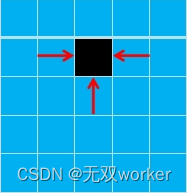f[i][j]=f[i-1][j]+f[i][j-1]+f[i][j+1]; ✘ 按照递推的规则，比如我们按照行列都从1开始推，在我们求f[i][j]位置的方案数之前，我们只知道f[i-1][j]和 f[i][j-1]的方案数，而不知道f[i][j+1]的方案数。

错误二： f[i][j]=f[i-1][j]+f[i][j-1]+f[i][j+1];✘

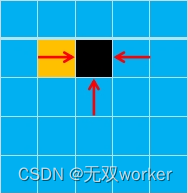陷阱：只能向左，上，右移动，并且移动过的方格马上就会塌陷，当上一步到达(i.j-1)的时候，他可以从(i,j)过来，即从右边过来，但是如果他从右边过来，那么下一步就不能再往左边走了，因为该方格已经塌陷了。即并不是走到 (i,j-1),(i,j+1)的方案都可以走到走到(i,j).所以递推公式错误

所以

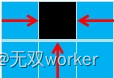我们分情况讨论：设走k步，最后一次向右走的方案数为r[k]；设走k步，最后一次向左走的方案数为l[k]; 设走k步，最后一次向上走的方案数为t[k]; 我们可以得到递推公式为： r[k]=t[k-1]+r[k-1];//上一步不可以向左走到达 l[k]=t[k-1]+l[k-1];//上一步不可以向右走到达 t[k]=t[k-1]+r[k-1]+l[k-1];//所有方案都可以

初始化： r[1]=1; l[1]=1; t[1]=1;

最终：f[k]=r[k]+l[k]+t[k];

我们可以把上面的等式化简：

r[k]=t[k-1]+r[k-1];//上一步不可以向左走到达

l[k]=t[k-1]+l[k-1];//上一步不可以向右走到达

t[k]=t[k-1]+r[k-1]+l[k-1];//所有方案都可以

r[k]+l[k]+t[k]=2*(t[k-1]+r[k-1]+t[k-1])+t[k-1];

f[k]=2*f[k-1]+t[k-1];

t[k-1]=t[k-2]+r[k-2]+l[k-2]=f[k-2];

最终得到：f[k]=2*f[k-1]+f[k-2]

初始值：f[0]=1; f[1]=3;

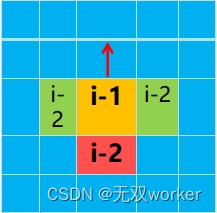其实把上文说人话就是当第i-1步走到表格中黄色的区域的位置的时候，方案数为f[i-1]; 第一种情况：无论是从哪个方向到达该位置，如果下一次(第i步)向上 (北)走,那么走i步的方案数是f[i-1] 第二种情况：如果上一次是从下方（红色)往上(北)走到达黄色位置，说明下一步(第k步)左边和右边都可以走，往上走的情况，第一种情况已经考虑了就不在重复计算了，方案数是f[i-2]*2. 第三种情况，如果上一次是从左边或者右边(绿色)到达黄色方格,说明下一次只可以往右或者左走(方向不变，向上已经考虑了。)，到达黄色方格的所有方案数是f[i-1]，再减去从下方到达黄色方格的方案数f[i-2]，即f[i-1] - f[i-2]

听懂了吗？没听懂再看一遍，一遍不行就两遍，我就不信你看不懂。

ACcode

#include<bits/stdc++.h>
using namespace std;
int f[25]={1,3,7};
int main(){int n;cin>>n;if (n==1||n==2){cout<<f[n];return 0;}for(int i=3;i<=n;i++){f[i]=f[i-1]*2+f[i-2];}cout<<f[n]<<endl;return 0;}

看了这么久，作者也写了这么久，能不能点一个赞，在收藏一下呢？最好的话在点个关注吧

谢谢啦！