本文主要是介绍具体数学之二项式系数2,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
又是一大堆公式来袭~~
二项级数的部分和另一种有意思的关系式子:
∑ k ⩽ m ( m + r k ) x k y m − k = ∑ k ≤ m ( − r k ) ( − x ) k ( x + y ) m − k , m 是 整 数 \sum_{k \leqslant m} \left( \begin{array}{c}{m+r} \\ {k}\end{array}\right) x^{k} y^{m-k}=\sum_{k \leq m} \left( \begin{array}{c}{-r} \\ {k}\end{array}\right)(-x)^{k}(x+y)^{m-k}, \quad m是整数 ∑k⩽m(m+rk)xkym−k=∑k≤m(−rk)(−x)k(x+y)m−k,m是整数
当m小于0时,两边均为0;当m=0时,两边都是1。
令左边部分为Sm,右边部分为Tm
S m = ∑ k ≤ m ( m − 1 + r k ) x k y m − k + ∑ k ⩽ m ( m − 1 + r k − 1 ) x k y m − k S_{m}=\sum_{k \leq m} \left( \begin{array}{c}{m-1+r} \\ {k}\end{array}\right) x^{k} y^{m-k}+\sum_{k \leqslant m} \left( \begin{array}{c}{m-1+r} \\ {k-1}\end{array}\right) x^{k} y^{m-k} Sm=∑k≤m(m−1+rk)xkym−k+∑k⩽m(m−1+rk−1)xkym−k
其中,
∑ k ⩽ m ( m − 1 + r k ) x k y m − k = ( m − 1 + r m ) x m + ∑ k ⩽ m − 1 ( m + 1 + r k ) x k y m − k = y S m − 1 + ( m − 1 + r m ) x m \sum_{k \leqslant m} \left( \begin{array}{c}{m-1+r} \\ {k}\end{array}\right) x^{k} y^{m-k}=\left( \begin{array}{c}{m-1+r} \\ {m}\end{array}\right) x^{m}+ \sum_{k \leqslant m-1} \left( \begin{array}{c}{m+1+r} \\ {k}\end{array}\right) x^{k} y^{m-k}=y S_{m-1}+\left( \begin{array}{c}{m-1+r} \\ {m}\end{array}\right) x^{m} ∑k⩽m(m−1+rk)xkym−k=(m−1+rm)xm+∑k⩽m−1(m+1+rk)xkym−k=ySm−1+(m−1+rm)xm
∑ k ≤ m ( m − 1 + r k − 1 ) x k y m − k = x ∑ k ≤ m ( m − 1 + r k − 1 ) x k − 1 y ( m − 1 ) − ( k − 1 ) = x S m − 1 \sum_{k \leq m} \left( \begin{array}{c}{m-1+r} \\ {k-1}\end{array}\right) x^{k} y^{m-k}=x\sum_{k \leq m} \left( \begin{array}{c}{m-1+r} \\ {k-1}\end{array}\right) x^{k-1} y^{(m-1)-(k-1)}=x S_{m-1} ∑k≤m(m−1+rk−1)xkym−k=x∑k≤m(m−1+rk−1)xk−1y(m−1)−(k−1)=xSm−1
因此, S m = ( x + y ) S m − 1 + ( − r m ) ( − x ) m S_{m}=(x+y) S_{m-1}+\left( \begin{array}{c}{-r} \\ {m}\end{array}\right)(-x)^{m} Sm=(x+y)Sm−1+(−rm)(−x)m

因此,可证明Sm和Tm是相等的!
∑ k ⩽ m ( m + r k ) ( − 1 ) k = ( − r m ) \sum_{k \leqslant m} \left( \begin{array}{c}{m+r} \\ {k}\end{array}\right)(-1)^{k}=\left( \begin{array}{c}{-r} \\ {m}\end{array}\right) ∑k⩽m(m+rk)(−1)k=(−rm),整数 m ⩾ 0 m \geqslant 0 m⩾0
相当于(5.16)
( r m ) ( m k ) = ( r k ) ( r − k m − k ) , m , k 是 整 数 \left( \begin{array}{c}{r} \\ {m}\end{array}\right) \left( \begin{array}{l}{m} \\ {k}\end{array}\right)=\left( \begin{array}{l}{r} \\ {k}\end{array}\right) \left( \begin{array}{l}{r-k} \\ {m-k}\end{array}\right), \quad m, k是整数 (rm)(mk)=(rk)(r−km−k),m,k是整数
( r m ) ( m k ) = r ! m ! ( r − m ) ! m ! k ! ( m − k ) ! = r ! k ! ( m − k ) ! ( r − m ) ! = r ! k ! ( r − k ) ! ( r − k ) ! k ! ( r − k ) ! ( r − k ) ! ( m − k ) ! ( r − m ) ! = ( r k ) ( r − k m − k ) \begin{aligned} \left( \begin{array}{c}{r} \\ {m}\end{array}\right) \left( \begin{array}{l}{m} \\ {k}\end{array}\right) &=\frac{r !}{m !(r-m) !} \frac{m !}{k !(m-k) !} \\ &=\frac{r !}{k !(m-k) !(r-m) !} \\ &=\frac{r !}{k !(r-k) !} \frac{(r-k) !}{k !(r-k) !} \frac{(r-k) !}{(m-k) !(r-m) !}=\left( \begin{array}{l}{r} \\ {k}\end{array}\right) \left( \begin{array}{l}{r-k} \\ {m-k}\end{array}\right) \end{aligned} (rm)(mk)=m!(r−m)!r!k!(m−k)!m!=k!(m−k)!(r−m)!r!=k!(r−k)!r!k!(r−k)!(r−k)!(m−k)!(r−m)!(r−k)!=(rk)(r−km−k)
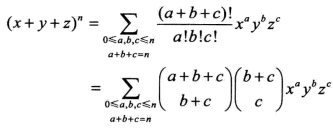
( a + b + c a , b , c ) = ( a + b + c ) ! a ! b ! c ! \left( \begin{array}{c}{a+b+c} \\ {a, b, c}\end{array}\right)=\frac{(a+b+c) !}{a ! b ! c !} (a+b+ca,b,c)=a!b!c!(a+b+c)!
多项式系数:
( a 1 + a 2 + ⋯ + a m a 1 , a 2 , ⋯   , a m ) = ( a 1 + a 2 + ⋯ + a m ) ! a 1 ! a 2 ! ⋯ a m ! \left( \begin{array}{c}{a_{1}+a_{2}+\cdots+a_{m}} \\ {a_{1}, a_{2}, \cdots, a_{m}}\end{array}\right)=\frac{\left(a_{1}+a_{2}+\cdots+a_{m}\right) !}{a_{1} ! a_{2} ! \cdots a_{m} !} (a1+a2+⋯+ama1,a2,⋯,am)=a1!a2!⋯am!(a1+a2+⋯+am)! = ( a 1 + a 2 + ⋯ + a m ! a 2 + ⋯ + a m ) ⋅ ( a m − 1 + a m a m ) =\left( \begin{array}{c}{a_{1}+a_{2}+\cdots+a_{m} !} \\ {a_{2}+\cdots+a_{m}}\end{array}\right) \cdot \left( \begin{array}{c}{a_{m-1}+a_{m}} \\ {a_{m}}\end{array}\right) =(a1+a2+⋯+am!a2+⋯+am)⋅(am−1+amam)

例子: ∑ k ( r m + k ) ( s n − k ) \sum_{k} \left( \begin{array}{c}{r} \\ {m+k}\end{array}\right) \left( \begin{array}{c}{s} \\ {n-k}\end{array}\right) ∑k(rm+k)(sn−k)
令 k 1 = m + k k_{1}=m+k k1=m+k
= ∑ k 1 − m ( r k 1 ) ( s n + m + k 1 ) \sum_{k_{1}-m} \left( \begin{array}{c}{r} \\ {k_{1}}\end{array}\right) \left( \begin{array}{c}{s} \\ {n+m+k1}\end{array}\right) ∑k1−m(rk1)(sn+m+k1)= ∑ k 1 − m ( r k 1 ) ( S n − ( k 1 − m ) ) \sum_{k1-m} \left( \begin{array}{l}{r} \\ {k_{1}}\end{array}\right) \left( \begin{array}{c}{S} \\ {n-(k1-m)}\end{array}\right) ∑k1−m(rk1)(Sn−(k1−m))
令 K 2 = n − k K_{2}=n-k K2=n−k
∑ n − k 2 ( r m + n − k 2 ) ( S k 2 ) \sum_{n-k_{2}} \left( \begin{array}{c}{r} \\ {m+n-k_{2}}\end{array}\right) \left( \begin{array}{l}{S} \\ {k_{2}}\end{array}\right) ∑n−k2(rm+n−k2)(Sk2)
上述表中的式子根本记不住的,其实就是范德蒙德卷积:
∑ k ( r k ) ( s n − k ) = ( r + s n ) , n 是 整 数 \sum_{k} \left( \begin{array}{c}{r} \\ {k}\end{array}\right) \left( \begin{array}{c}{s} \\ {n-k}\end{array}\right)=\left( \begin{array}{c}{r+s} \\ {n}\end{array}\right), \quad n是整数 ∑k(rk)(sn−k)=(r+sn),n是整数

这篇关于具体数学之二项式系数2的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



