【C++】分披萨

(为了调试程序方便，程序中放了很多输出，可以适当删掉)

题目描述及分析

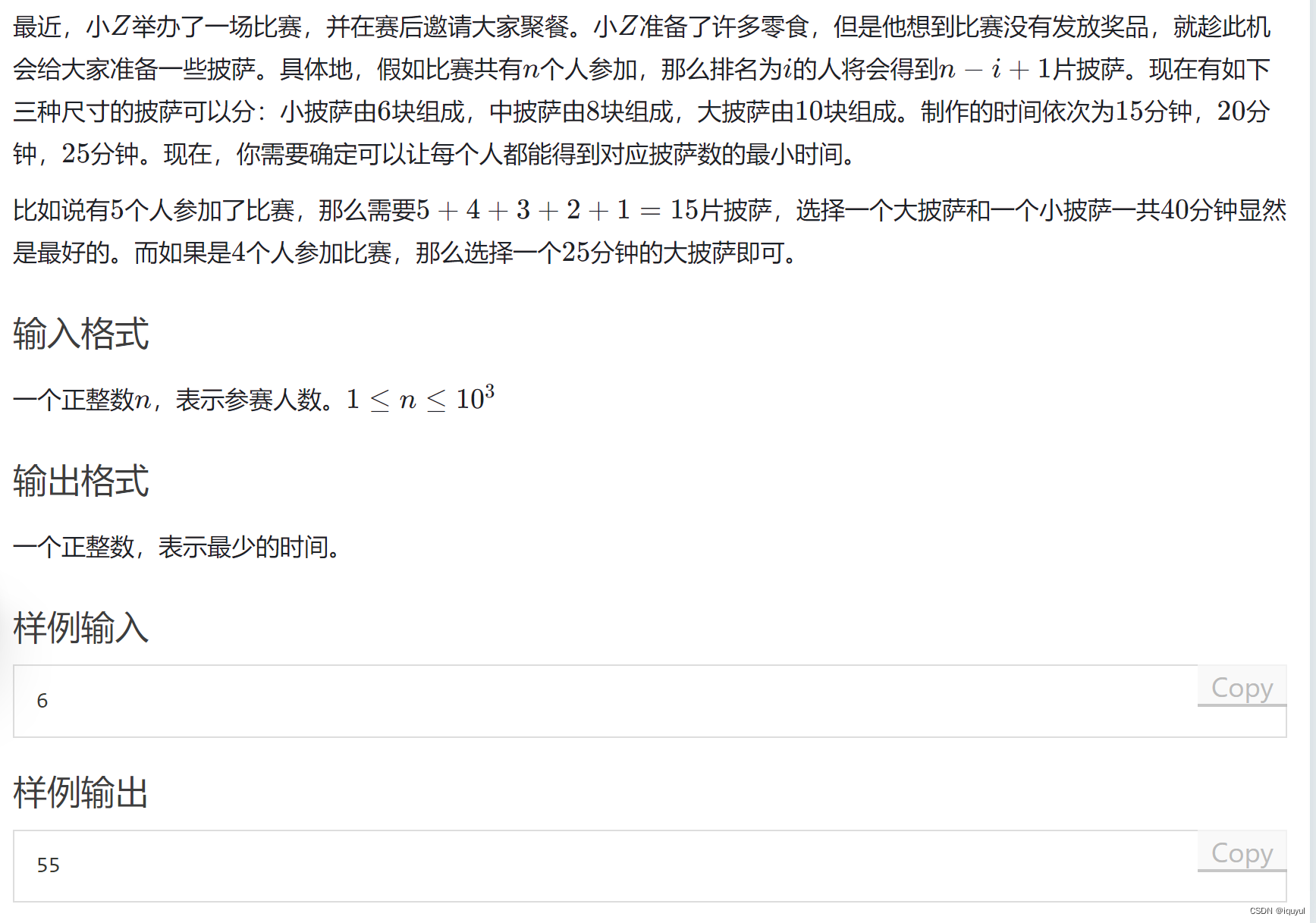  这个问题主要分为两部分。
  首先是计算n个人一共需要多少块蛋糕，只需要对等差数列求和。
  接下来是选择时间最少的方案，制作足够数量的披萨。这里有数量和时间两个约束条件，但是如果用制作的时间除以披萨的数量我们可以发现，三种披萨对应的结果都是2.5，也就是说制作每一种披萨的效率都是一样的。或者说，披萨制作的时间与数量成正比，约束条件可以改成“选择能制作足够数量并数量最少的方案”。

题解1

  首先想到的办法，就是像乌鸦喝水一样，先扔大石子，再扔小石子，提高瓶子的利用率。这里也是一样，首先求出至少需要多少块大披萨，再逐渐将大披萨换成其他种类的小披萨。换成小披萨时，判定条件设为题目的约束条件，循环判定即可。

#include<iostream>
#include<cstring>
using namespace std;int m;	//变量m表示全部用大披萨需要的数量
int n, cnt = 0;//n表示人数
int Time, Num;//最终需要的时间和数量
int v[3] = { 10,8,6 }, w[3] = { 25,20,15 };// v[]表示披萨型号对应的块数，w[]表示披萨型号对应的时间int main() {cout << "请输入获奖人数：" << endl;cin >> n;for (int i = 1; i <= n; i++)	cnt += i;cout << "一共需要的块数为：" << cnt << "块" << endl;m = (cnt % v[0]) ? (cnt / v[0] + 1) : (cnt / v[0]);// 先用大披萨满足数量条件Time = m * w[0];Num = m * v[0];cout << "至少需要大披萨" << m << "块" << endl;for (int i = 1; i < 3; i++) {// 这里只要考虑剩下两种while ((Num - v[i - 1] + v[i] >= cnt) && (Time - w[i - 1] + w[i] <= Time)) { // 两个判断，数量是否足够，时间是否更少Num = Num - v[i - 1] + v[i];Time = Time - w[i - 1] + w[i];cout << "取出" << v[i - 1] << "块" << endl;cout << "加入" << v[i] << "块" << endl;cout << "所需要的时间为：" << Time << "分钟" << endl;}}cout << "所需要的最短时间为：" << Time << "分钟" << endl;return 0;
}

题解2

  题解1的约束条件依然是时间和空间，可以都改为时间，优化掉一个变量。

#include<iostream>
#include<cstring>
using namespace std;int n, m;
int cnt = 0;
double Time;
int v[3] = { 10,8,6 }, w[3] = { 25,20,15 };int main() {cout << "请输入获奖人数：" << endl;cin >> n;for (int i = 1; i <= n; i++)	cnt += i;cout << "一共需要的块数为：" << cnt << "块" << endl;m = (cnt % v[0]) ? (cnt / v[0] + 1) : (cnt / v[0]);// 先用大披萨满足数量条件Time = m * w[0];cout << "至少需要大披萨" << m << "块" << endl;for (int i = 1; i < 3; i++) {// 这里只要考虑剩下两种while ((Time - w[i - 1] + w[i] >= cnt * 2.5) && (Time - w[i - 1] + w[i] <= Time)) { // 两个判断，数量是否足够，时间是否更少Time = Time - w[i - 1] + w[i];cout << "减少" << w[i - 1] << "分钟" << endl;cout << "增加" << w[i] << "分钟" << endl;cout << "所需要的时间为：" << Time << "分钟" << endl;}}cout << "所需要的最短时间为：" << Time << "分钟" << endl;return 0;
}

题解3

  观察题解2的代码可以发现

while ((Time - w[i - 1] + w[i] >= cnt * 2.5) && (Time - w[i - 1] + w[i] <= Time)) {Time = Time - w[i - 1] + w[i];……
}

  这里的判断条件和赋值语句有重复，可以用min（）函数稍微优化一下。

#include<iostream>
#include<cstring>
using namespace std;const int N = 1010;
int n, m;
int cnt = 0;
double Time;
int v[3] = { 10,8,6 }, w[3] = { 25,20,15 };int main() {cout << "请输入获奖人数：" << endl;cin >> n;for (int i = 1; i <= n; i++)	cnt += i;cout << "一共需要的块数为：" << cnt << "块" << endl;m = (cnt % v[0]) ? (cnt / v[0] + 1) : (cnt / v[0]);// 先用大披萨满足数量条件Time = m * w[0];cout << "至少需要大披萨" << m << "块" << endl;for (int i = 1; i < 3; i++) {// 这里只要考虑剩下两种while (Time - w[i - 1] + w[i] >= cnt * 2.5) {Time = min(Time, Time - w[i - 1] + w[i]);cout << "减少" << w[i - 1] << "分钟" << endl;cout << "增加" << w[i] << "分钟" << endl;cout << "所需要的时间为：" << Time << "分钟" << endl;}}cout << "所需要的最短时间为：" << Time << "分钟" << endl;return 0;
}

题解4

  这里我们先看一下，n=10时题解3的运行结果。

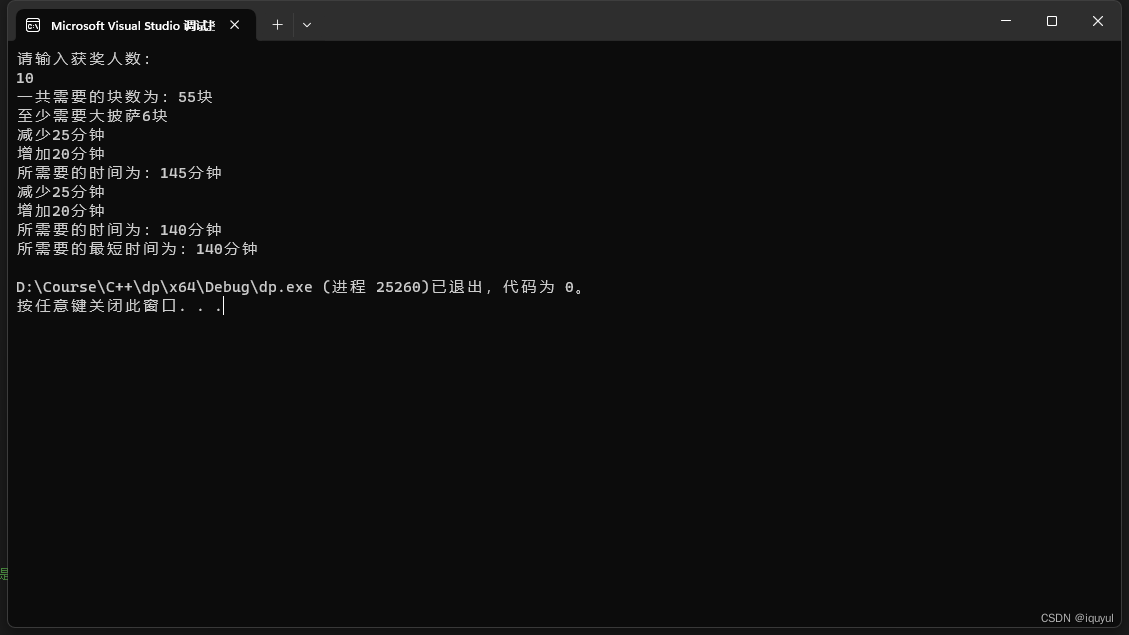
  我们发现，每一次对披萨型号的调整，实际都是将一块大披萨换成中披萨，时间减少5分钟，直到刚好满足时间条件。
  于是，循环可以再一次修改,直接判断是否可以继续更改披萨型号，即时间减少五分钟后是否还能够满足最低要求。
  同时，也不需要再考虑中披萨和小披萨所需要的具体时间，相关数组可以删掉。

#include<iostream>
#include<cstring>
using namespace std;int n, m;
int cnt = 0;
double Time;
int j = 0;int main() {cout << "请输入获奖人数：" << endl;cin >> n;for (int i = 1; i <= n; i++)	cnt += i;cout << "一共需要的块数为：" << cnt << "块" << endl;m = (cnt % 10) ? (cnt / 10 + 1) : (cnt / 10);// 先用大披萨满足数量条件Time = m * 25;cout << "至少需要大披萨" << m << "块" << endl;while (Time - 5 > cnt * 2.5) {Time -= 5;j++;cout << "调整" << j << "次型号" << endl;}cout << "所需要的最短时间为：" << Time << "分钟" << endl;return 0;
}