【优化求解】基于Levy飞行的飞蛾扑火优化算法(LMFO)求解单目标优化问题附matlab代码

1 简介

由于飞蛾扑火优化 （ＭＦＯ）算法收敛速度和计算精度还有待提高，提出一种改进的基于 Ｌéｖｙ飞行轨迹的飞蛾扑火优化 （ＬＭＦＯ）算法。增强局部搜索能力，大幅度提升收敛速度和求解精度。对１２个无约束基准函数进行实验测试，测试结果表明，改进后的 ＬＭＦＯ 是有效可行的。群智能算法一般来源于对自然界中一些生物群体行为的模仿，因其具有传统优化方法所不具有的优点，已 发展成为优化问题中的研究热点。飞蛾扑火优化 （ｍｏｔｈ－ｆｌａｍｅｏｐｔｉｍｉｚａｔｉｏｎ，ＭＦＯ算法是由 Ｍｉｒｊａｌｉｌｉ提出的一种启发式优化算法，此算法的灵感来源于飞蛾在夜间一种奇特的导航方式。夜间飞蛾以月亮为参考物来辨别方向，当 飞 蛾 迷失方向的时候，只需根据月光来自己调整身体的方位，便能找到之前的 方 向。因其与月亮相距甚远，所 以 此 机 制 能确保沿直线运 动。在 现 实 世 界 里，飞蛾常常把人造光误 认为是月亮所发出 的 光，于是飞蛾便会绕着人造光作螺旋状盘旋，这就是时常会看到飞蛾绕着人造光作螺旋形移动的原因，同时也说明了横向定位的低效性。

在基本 ＭＦＯ 算 法 中，假设飞蛾是候选解，矩 阵 Ｍ 表示飞蛾的集合，数组ＯＭ 用于存储相应的适应度值。该 算法的另外一个核心组件是火焰，火 焰 矩 阵 用 Ｆ 表 示，且 数组 Ｍ 和Ｆ 的 维 数 相 等，数 组 ＯＦ 用来存储相应的适应度值。在这里，飞蛾和火焰都是解。它 们 之 间 不 同 之 处 就 是在每一次迭代过程中对待和更新它们的方式不同。飞 蛾 是在搜索空间里移动的实际搜索主体，而火焰是飞蛾到目前为止获取的 最 佳 位 置。因 此，倘 若 找 到 一 个 更 好 的 解，每只飞蛾便在标记附近搜索并更新它。通 过 此 机 制，飞 蛾 永远不会错过它的最优解。

2 部分代码

%______________________________________________________________________________________________

%  Moth-Flame Optimization Algorithm (MFO) toolbox                                                            

%  Source codes demo version 1.0                                                                      

%                                                                                                     

%  Developed in MATLAB R2011b(7.13)                                                                   

%                                                                                                     

%  Author and programmer: Seyedali Mirjalili                                                          

%                                                                                                     

%         e-Mail: ali.mirjalili@gmail.com                                                             

%                 seyedali.mirjalili@griffithuni.edu.au                                               

%                                                                                                     

%       Homepage: http://www.alimirjalili.com                                                         

%                                                                                                     

%  Main paper:                                                                                        

%  S. Mirjalili, Moth-Flame Optimization Algorithm: A Novel Nature-inspired Heuristic Paradigm, 

%  Knowledge-Based Systems, DOI: http://dx.doi.org/10.1016/j.knosys.2015.07.006

%_______________________________________________________________________________________________

% You can simply define your cost in a seperate file and load its handle to fobj 

% The initial parameters that you need are:

%__________________________________________

% fobj = @YourCostFunction

% dim = number of your variables

% Max_iteration = maximum number of generations

% SearchAgents_no = number of search agents

% lb=[lb1,lb2,...,lbn] where lbn is the lower bound of variable n

% ub=[ub1,ub2,...,ubn] where ubn is the upper bound of variable n

% If all the variables have equal lower bound you can just

% define lb and ub as two single number numbers

% To run MFO: [Best_score,Best_pos,cg_curve]=MFO(SearchAgents_no,Max_iteration,lb,ub,dim,fobj)

%______________________________________________________________________________________________

function [Best_flame_score,Best_flame_pos,Convergence_curve]=MFO(N,Max_iteration,lb,ub,dim,fobj,handles,value)

display('MFO is optimizing your problem');

%Initialize the positions of moths

Moth_pos=initialization(N,dim,ub,lb);

Convergence_curve=zeros(1,Max_iteration);

Iteration=1;

% Main loop

while Iteration<Max_iteration+1

    

    % Number of flames Eq. (3.14) in the paper

    Flame_no=round(N-Iteration*((N-1)/Max_iteration));

    

    for i=1:size(Moth_pos,1)

        

        % Check if moths go out of the search spaceand bring it back

        Flag4ub=Moth_pos(i,:)>ub;

        Flag4lb=Moth_pos(i,:)<lb;

        Moth_pos(i,:)=(Moth_pos(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;  

        

        % Calculate the fitness of moths

        Moth_fitness(1,i)=fobj(Moth_pos(i,:));

        All_fitness(1,i)=Moth_fitness(1,i);

        

    end

       

    if Iteration==1

        % Sort the first population of moths

        [fitness_sorted I]=sort(Moth_fitness);

        sorted_population=Moth_pos(I,:);

        

        % Update the flames

        best_flames=sorted_population;

        best_flame_fitness=fitness_sorted;

    else

        

        % Sort the moths

        double_population=[previous_population;best_flames];

        double_fitness=[previous_fitness best_flame_fitness];

        

        [double_fitness_sorted I]=sort(double_fitness);

        double_sorted_population=double_population(I,:);

        

        fitness_sorted=double_fitness_sorted(1:N);

        sorted_population=double_sorted_population(1:N,:);

        

        % Update the flames

        best_flames=sorted_population;

        best_flame_fitness=fitness_sorted;

    end

    

    % Update the position best flame obtained so far

    Best_flame_score=fitness_sorted(1);

    Best_flame_pos=sorted_population(1,:);

      

    previous_population=Moth_pos;

    previous_fitness=Moth_fitness;

    

    % a linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)

    a=-1+Iteration*((-1)/Max_iteration);

    

    for i=1:size(Moth_pos,1)

        

        for j=1:size(Moth_pos,2)

            if i<=Flame_no % Update the position of the moth with respect to its corresponsing flame

                

                % D in Eq. (3.13)

                distance_to_flame=abs(sorted_population(i,j)-Moth_pos(i,j));

                b=1;

                t=(a-1)*rand+1;

                

                % Eq. (3.12)

                Moth_pos(i,j)=distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(i,j);

            end

            

            if i>Flame_no % Upaate the position of the moth with respct to one flame

                

                % Eq. (3.13)

                distance_to_flame=abs(sorted_population(i,j)-Moth_pos(i,j));

                b=1;

                t=(a-1)*rand+1;

                

                % Eq. (3.12)

                Moth_pos(i,j)=distance_to_flame*exp(b.*t).*cos(t.*2*pi)+sorted_population(Flame_no,j);

            end

            

        end

        

    end

    

    Convergence_curve(Iteration)=Best_flame_score;

    

     if Iteration>2

        line([Iteration-1 Iteration], [Convergence_curve(Iteration-1) Convergence_curve(Iteration)],'Color','b')

        xlabel('Iteration');

        ylabel('Best score obtained so far');        

        drawnow

    end

    

    set(handles.itertext,'String', ['The current iteration is ', num2str(Iteration)])

    set(handles.optimumtext,'String', ['The current optimal value is ', num2str(Best_flame_score)])

    if value==1

        hold on

        scatter(Iteration*ones(1,N),All_fitness,'.','k')

    end

    

    Iteration=Iteration+1; 

end

3 仿真结果

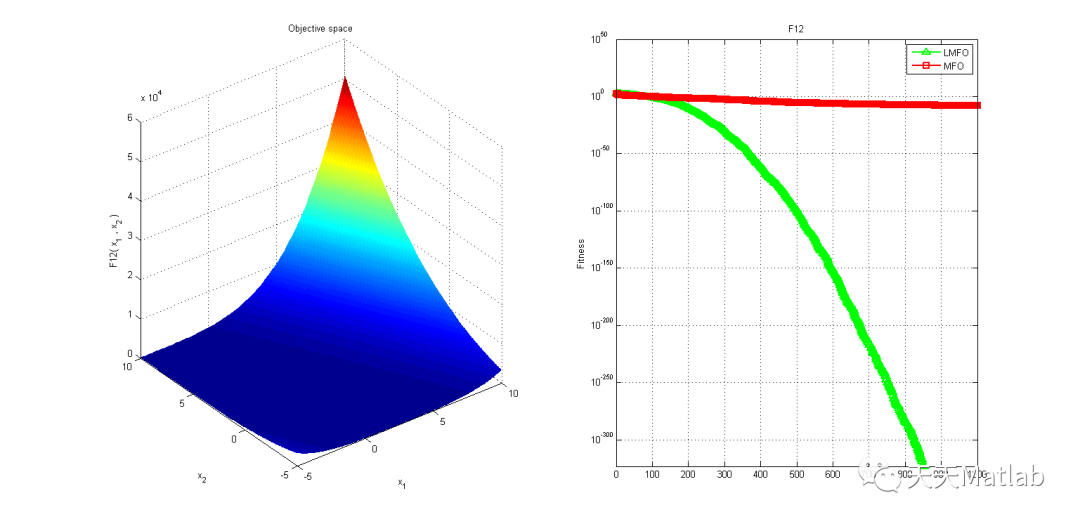
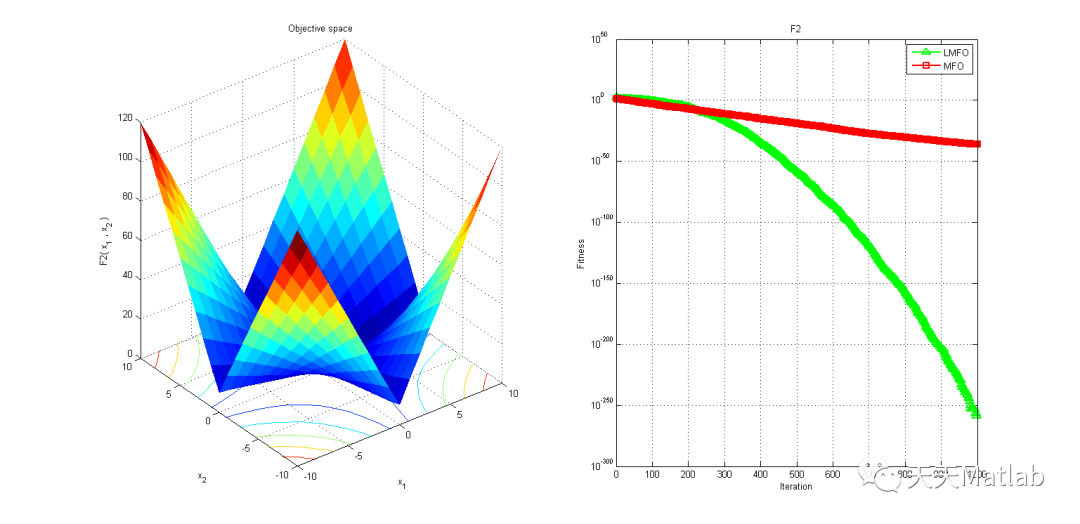
4 参考文献

[1]李志明,莫愿斌.基于Lévy飞行的飞蛾扑火优化算法[J].计算机工程与设计,2017,38(03):807-813.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。