本文主要是介绍【数据结构】二叉查找树和平衡二叉树，以及二者的区别，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
目录
1、二叉查找树
1.1、定义
1.2、查找二叉树的优点
1.2、查找二叉树的弊端
2、平衡二叉树
2.1、定义
2.2、 实现树结构平衡的方法（旋转机制）
2.2.1、左旋
2.2.2、右旋
3、总结
1、二叉查找树
二叉查找树又名二叉排序树，亦称二叉搜索树。是每个结点最多有两个子树的树结构，通常子树被称作“左子树”和“右子树”。
1.1、定义
二叉查找树的定义：
- 若左子树不空，则左子树上所有节点的值均小于它的根节点的值；
- 若右子树不空，则右子树上所有节点的值均大于它的根节点的值；
- 左、右子树也分别为二叉排序树；
- 没有键值相等的节点。
1.2、查找二叉树的优点
普通二叉树和二叉查找树示例图如下所示：
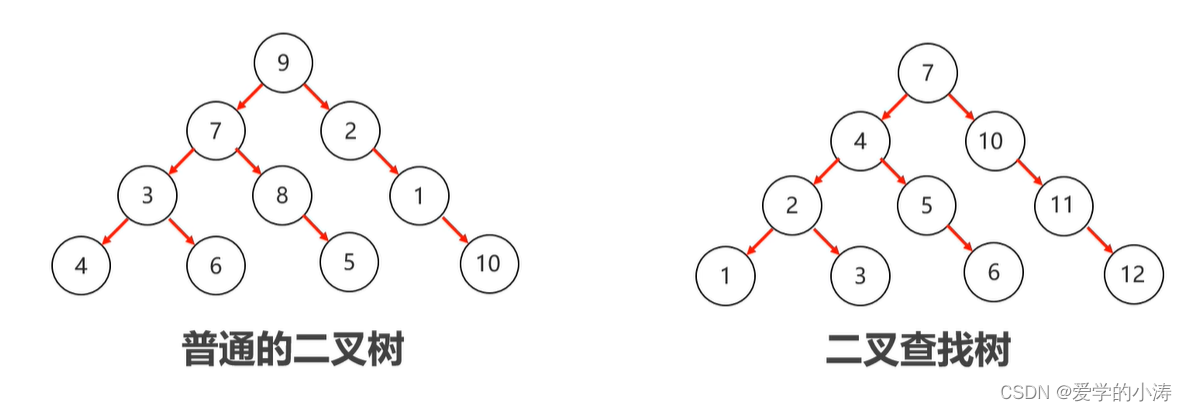
上图中左边为普通二叉树，它的弊端是对数据的插入没有要求，在进行数据的查找时就非常的麻烦，因为它里面的数据没有什么规律让我们进行查找。普通的二叉树如果想要查找数据的话就只能进行遍历，查找的效率非常的低。
所以就有了上图中右边的二叉查找树，因为二叉查找树插入数据的时的规律是：小的存左边；大的存右边；一样的不存，并且它在查找数据的时候也是按照这个规律来进行查找的
1.2、查找二叉树的弊端
现有数字{ 3，6，7，9，10，11，12 } ，基于这些数字生成二叉查找树如下：
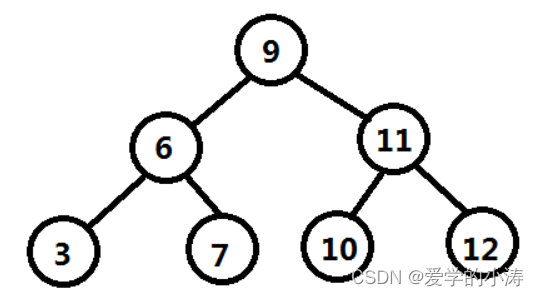
这时候看起来二叉树的结构是很均匀的排列的，但是当依次插入13,14数据后，如下图：
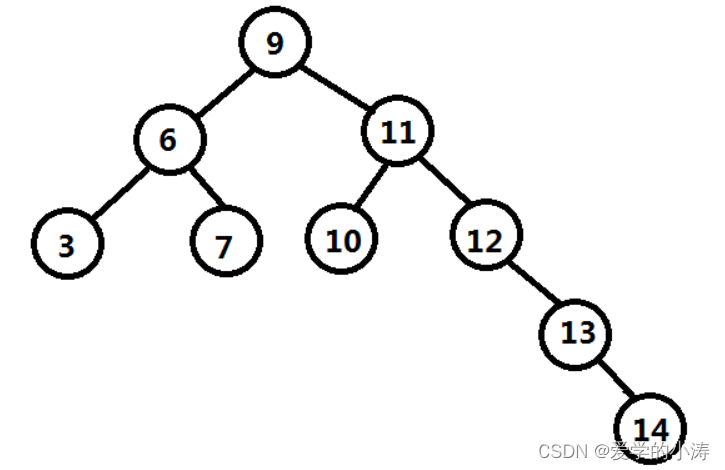
这时候发现，由于二叉树的根节点是确定不变的，所以当调整数据的插入或删除顺序，会造成二叉树朝着单项链表的方向发展（张歪了，变成歪脖子树了），大大降低了数据的查询效率。一棵树要提高查询效率，左右的高度要差不多才可以。那问题是在添加节点的时候，如何保证把它变成左右高度差不多长的这种树呢？这时候就出现了下面的平衡二叉树。
2、平衡二叉树
平衡二叉树是基于二叉查找树优化而来的。
2.1、定义
非叶子结点最多只能有两个子结点，且左边子结点点小于当前结点值，右边子结点大于当前结点树，并且为保证查询性能增增删结点时要保证左右两边结点层级相差不大于1，具体实现有AVL、Treap、红黑树等。Java中TreeMap就是基于红黑树实现的。
也就是说平衡二叉树是在二叉查找树的基础上又多了一个规则：任意节点左右子树高度差不超过1。
判断是否为平衡二叉树示例：
示例1：
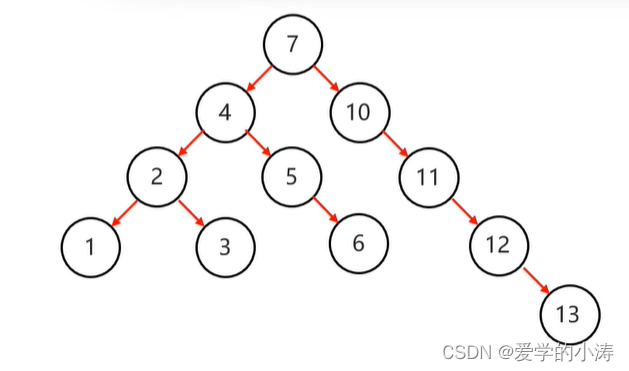
上图中的二叉树是一个查找二叉树，但不是平衡二叉树。虽然根节点7的左子树高度为3，右子树高度为4，左右子树高度差不超过1。但平衡二叉树是需要任意节点都满足这个规则，比如节点10就不满足这个规则，节点10的左子树高度为0，右子树高度为3，左右子树高度差明显超过1了，所以它不是平衡二叉树。
示例2：
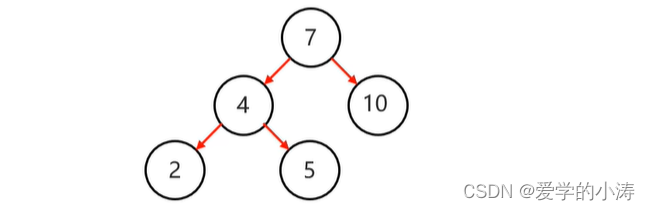
上图中的二叉树是一个平衡二叉树，因为它满足查找二叉树的同时还满足了规则：任意节点左右子树高度差不超过1。
2.2、 实现树结构平衡的方法（旋转机制）
旋转机制右两种，分别是左旋和右旋。旋转机制的触发时机为：当添加一个节点之后，该树不再是一颗平衡二叉树时
2.2.1、左旋
左旋的步骤
先确定支点：从添加的节点开始，不断的往父节点找不平衡的节点
找到不平衡的节点后：
（1）若不平衡的节点没有左子树，以不平衡的点作为支点，把支点左旋降级，变成左子节点，晋升原来的右子节点
（2）若不平衡的节点有左子树，以不平衡的点作为支点，将根节点的右侧往左拉，原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右子节点
左旋示例
示例1：
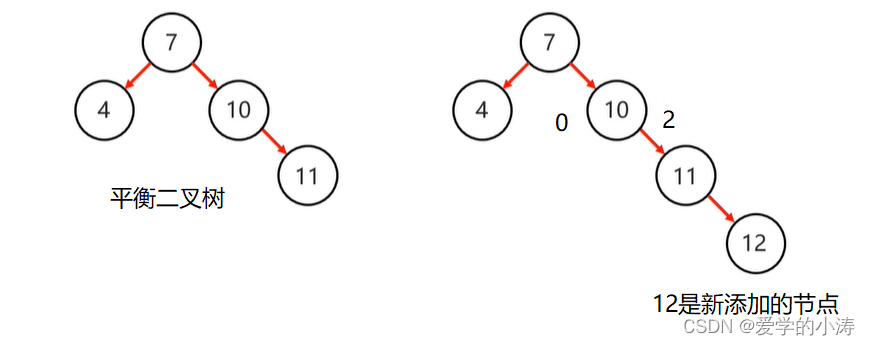
上图中左边的平衡二查树添加了节点12后，变成了右边的结构，这时候平衡被破坏了，所以要进行旋转。
先确定支点：从添加的节点12开始，不断的往父节点找不平衡的节点。我们发现节点10的左子树高度为0，右子树高度为2，所以找到不平衡的节点10。
找到不平衡的节点：不平衡的节点10没有左子树，以不平衡的点作为支点，把支点左旋降级，变成左子节点，晋升原来的右子节点
如下图所示：
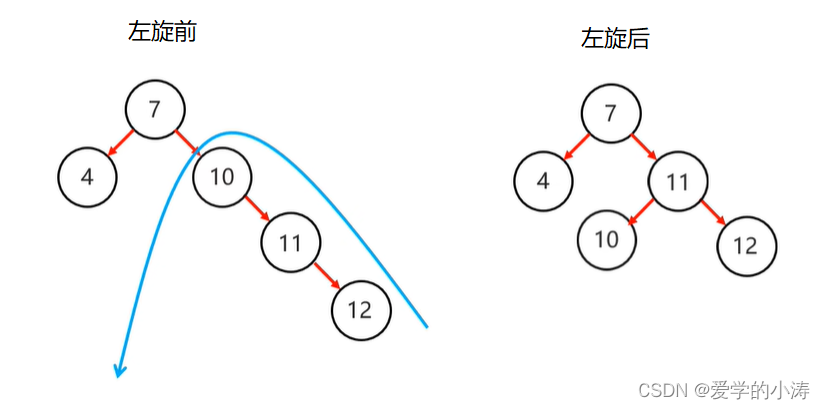
通过左旋后就保持平衡了，还是一个平衡二叉树
示例2：
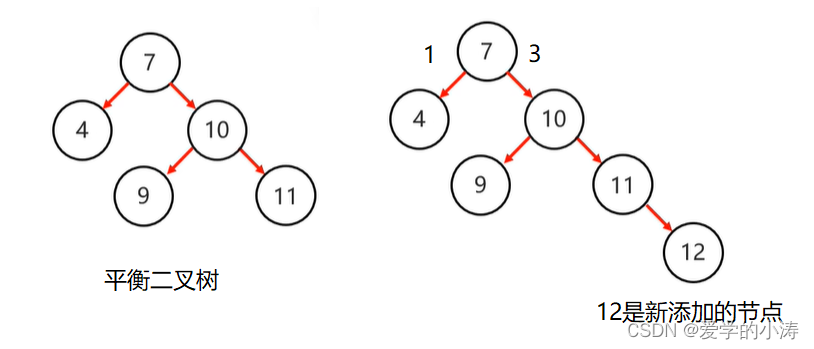
上图中左边的平衡二查树添加了节点12后，变成了右边的结构，这时候平衡被破坏了，所以要进行旋转。
先确定支点：从添加的节点12开始，不断的往父节点找不平衡的节点。我们发现节点7的左子树高度为1，右子树高度为3，所以找到不平衡的节点7。
找到不平衡的节点：不平衡的节点7有左子树，以不平衡的点作为支点，将根节点的右侧往左拉，原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右子节点
如下图所示：
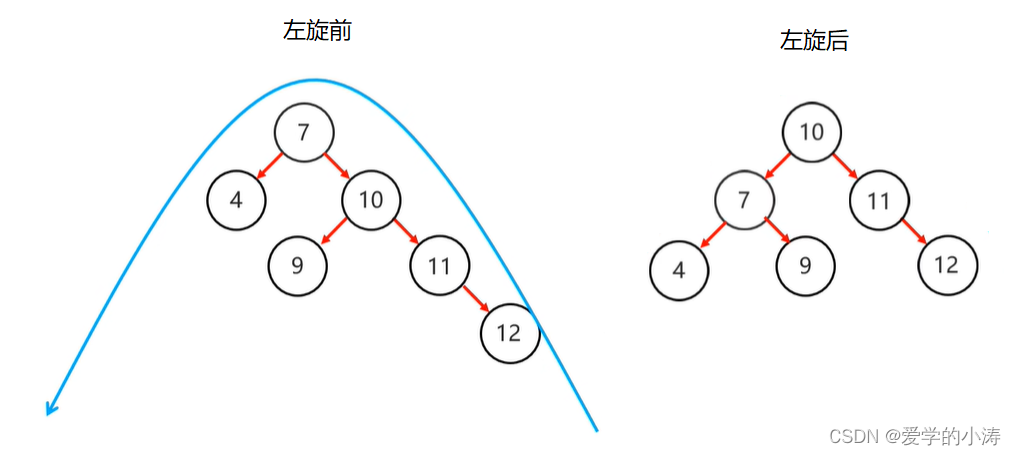
通过左旋后就保持平衡了，还是一个平衡二叉树
2.2.2、右旋
右旋的步骤
先确定支点：从添加的节点开始，不断的往父节点找不平衡的节点
找到不平衡的节点后：
（1）若不平衡的节点没有右子树，以不平衡的点作为支点，把支点右旋降级，变成右子节点，晋升原来的左子节点
（2）若不平衡的节点有左子树，以不平衡的点作为支点，将根节点的左侧往右拉，原先的左子节点变成新的父节点，并把多余的右子节点出让，给已经降级的根节点当左子节点
右旋示例
示例1：
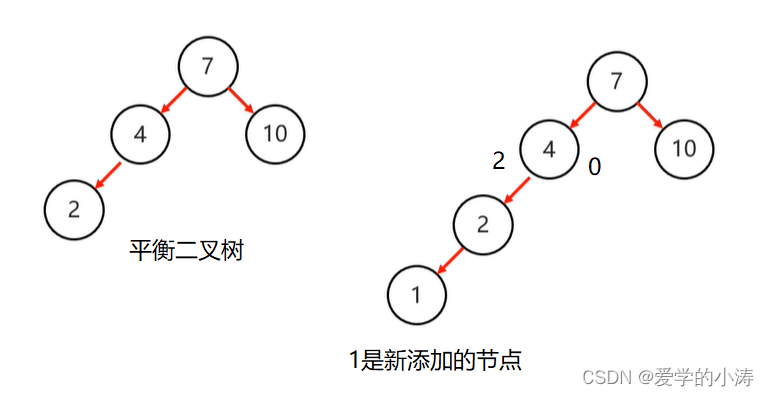
上图中左边的平衡二查树添加了节点1后，变成了右边的结构，这时候平衡被破坏了，所以要进行旋转。
先确定支点：从添加的节点1开始，不断的往父节点找不平衡的节点。我们发现节点4的左子树高度为2，右子树高度为0，所以找到不平衡的节点4。
找到不平衡的节点：不平衡的节点4有左子树，以不平衡的点作为支点，将根节点的右侧往左拉，原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右子节点
如下图所示：
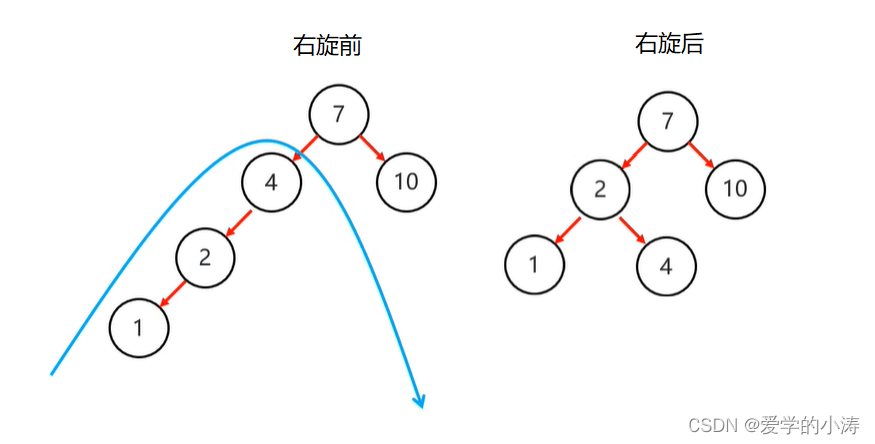
通过右旋后就保持平衡了，还是一个平衡二叉树
示例2：
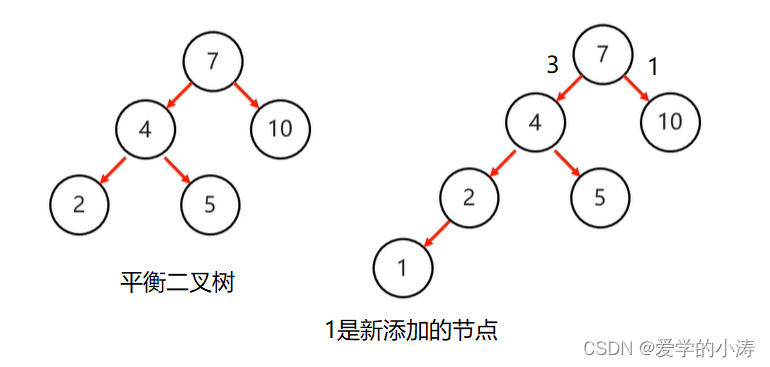
上图中左边的平衡二查树添加了节点1后，变成了右边的结构，这时候平衡被破坏了，所以要进行旋转。
先确定支点：从添加的节点1开始，不断的往父节点找不平衡的节点。我们发现节点7的左子树高度为3，右子树高度为1，所以找到不平衡的节点7。
找到不平衡的节点：不平衡的节点7有左子树，以不平衡的点作为支点，将根节点的右侧往左拉，原先的右子节点变成新的父节点，并把多余的左子节点出让，给已经降级的根节点当右子节点
如下图所示：
通过右旋后就保持平衡了，还是一个平衡二叉树
3、总结
相同点：都是基于分治思想采用二分法的策略提高数据查找速度的二叉树结构。
不同点：
- 二叉查找树的根节点是不可变的，左右两边结点层级差没有限制；
- 平衡二叉树左右两边结点层级相差不大于1，通过旋转实现根节点可变，达到自平衡。
相对于二叉查找树，平衡二叉树的查询效率高，但由于增加和删除节点时，为了保证自平衡会做连续的旋转操作，平衡二叉树的额外开销比较大，耗时相对较长。
推荐：
【数据结构】前缀树的模拟实现-CSDN博客
https://blog.csdn.net/m0_65277261/article/details/136086068?spm=1001.2014.3001.5501
【计算机组成原理】存储器知识-CSDN博客https://blog.csdn.net/m0_65277261/article/details/134770339?spm=1001.2014.3001.5501
java数据结构（哈希表—HashMap）含LeetCode例题讲解_leetcode hashmap.values()-CSDN博客https://blog.csdn.net/m0_65277261/article/details/134712832?spm=1001.2014.3001.5501
这篇关于【数据结构】二叉查找树和平衡二叉树，以及二者的区别的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
