本文主要是介绍时间序列预测模型:ARIMA模型,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. ARIMA模型原理介绍
ARIMA模型,全称为自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model),是一种常用的时间序列预测方法。ARIMA模型通过对时间序列数据的差分化处理,使非平稳时间序列数据变得平稳,进而利用自回归(AR) 和滑动平均(MA) 模型对其进行建模和预测。ARIMA模型可以表示为ARIMA(p, d, q),其中:
p:自回归项的阶数,表示预测值与过去值之间的关系。
d:差分次数,使序列平稳所需的差分次数。
q:移动平均项的阶数,表示预测误差与过去误差之间的关系。
2. 实例分析
接下来我们使用一个销售数据来进行ARIMA预测,数据第1列为日期,第2列为销量,利用现有数据预测未来10天的销量数据。
(1)首先读取数据,如何绘制历史数据变化趋势图。
clc,clear
T = readtable('arima_data.xls');
T.Properties.VariableNames
dates=T.x__
sales=T.x___1
plot(dates, sales);
xlabel('日期');
ylabel('销量');
title('销量随时间的变化');
结果如下:

(2)进行平稳性检验、ACF检验、PACF检验,然后确定最合适的p、d、q组合。
% 使用 adftest 检查平稳性
isStationary = adftest(sales);
if ~isStationary% 如果非平稳,进行一阶差分salesDiff = diff(sales);% 重新检查差分后序列的平稳性isStationary = adftest(salesDiff);% 如果还是非平稳,可能需要进行更多的差分操作
end
% 绘制ACF和PACF图
figure;
subplot(2,1,1);
autocorr(salesDiff); % 对差分后的序列绘制ACF图
subplot(2,1,2);
parcorr(salesDiff); % 对差分后的序列绘制PACF图
% 尝试多个p和q的组合
minBIC = Inf;
bestModel = [];
for p = 0:3 % 假设测试p的范围为0到3for q = 0:3 % 假设测试q的范围为0到3model = arima(p,1,q);[fit,~,logL] = estimate(model, sales, 'Display', 'off');[aic,bic] = aicbic(logL, p+q+1, length(sales));if bic < minBICminBIC = bic;bestModel = fit;endend
end
bestModel
平稳性检验: 非平稳
ACF检验和PACF检验:
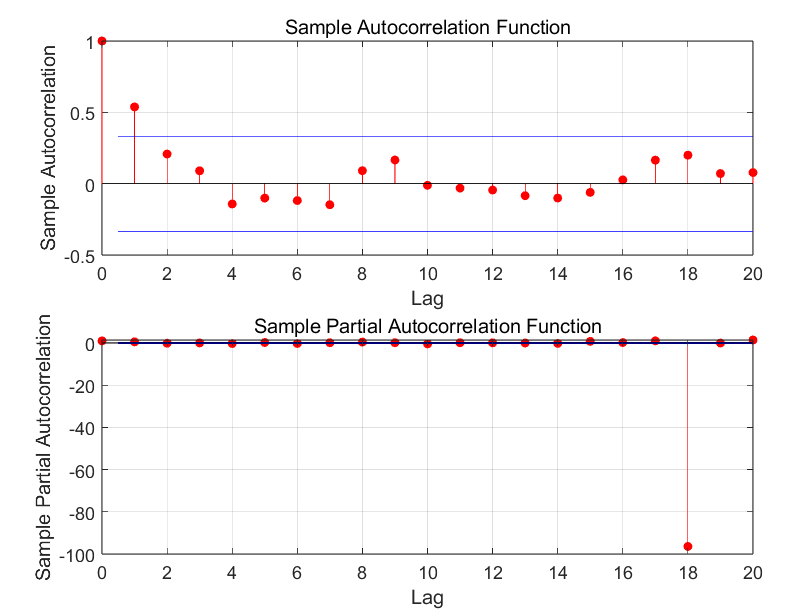
最优模型:

(3)建立模型进行预测
model = arima(1,1,0); % ARIMA(1,1,0)模型
fitModel = estimate(model, sales);
numPeriods = 10; % 预测未来10个时间点
[forecast, ~, ~] = forecast(fitModel, numPeriods, 'Y0', sales)
futureDates = dates(end) + (1:numPeriods)' % 生成未来日期
figure;
plot([dates;futureDates(1)], [sales;forecast(1)], 'b', futureDates, forecast, 'r'); % 绘制实际销量和预测销量
xlabel('日期');
ylabel('销量');
legend({'实际销量', '预测销量'}, 'Location', 'best');
title('销量预测');
ARIMA(1,1,0)模型:
ARIMA(1,1,0) Model (Gaussian Distribution):Value StandardError TStatistic PValue _______ _____________ __________ __________Constant 23.116 13.829 1.6716 0.094607
AR{1} 0.54589 0.11588 4.711 2.465e-06
Variance 5389.9 1084.4 4.9705 6.6791e-07
预测结果图:
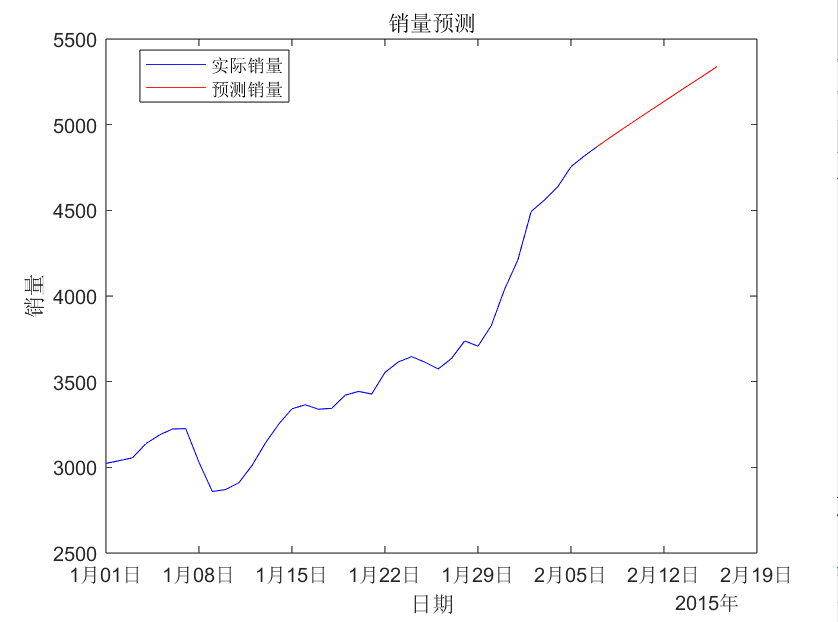
这篇关于时间序列预测模型:ARIMA模型的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





