本文主要是介绍特征模型仿真例1:参数辨识,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
摘要 多种不同信号输入一个稳定的4阶系统,根据系统的输入和输出信号建立参考特征模型并使用最小二乘法辨识参数,比较多种输入信号下的辨识结果。
专栏全部文章见 基于特征模型的全系数自适应控制。
题目
考虑被控对象
G ( s ) = 3 s + 4 s 4 + 5 s 3 + 10 s 2 + 6 s + 4 G(s)=\frac{3 s+4}{s^{4}+5 s^{3}+10 s^{2}+6 s+4} G(s)=s4+5s3+10s2+6s+43s+4
和特征模型
y ( k ) = ϕ T ( k − 1 ) θ ( k ) y(k)=\boldsymbol{\phi}^{\mathrm{T}}(k-1)\boldsymbol{\theta}(k) y(k)=ϕT(k−1)θ(k)
其中
ϕ ( k − 1 ) = [ y ( k − 1 ) y ( k − 2 ) u ( k − 1 ) ] T θ ( k ) = [ f 1 ( k ) f 2 ( k ) g 0 ( k ) ] T \begin{aligned} \phi(k-1) =& [\begin{matrix} y(k-1) & y(k-2) & u(k-1) \end{matrix}]^{\mathrm{T}} \\ \theta(k) =& [\begin{matrix} f_{1}(k) & f_{2}(k) & g_{0}(k) \end{matrix}]^{\mathrm{T}} \end{aligned} ϕ(k−1)=θ(k)=[y(k−1)y(k−2)u(k−1)]T[f1(k)f2(k)g0(k)]T
控制输入 u u u 取如下四种形式:
- 阶跃信号 u ( k ) = 10 u(k)=10 u(k)=10;
- 经 “平滑” 的阶跃信号 u ( k ) = 0.97 u ( k − 1 ) + 0.3 u(k)=0.97u(k-1)+0.3 u(k)=0.97u(k−1)+0.3;
- 周期为 1 1 1 的正弦信号 u ( k ) = 10 cos ( 2 π k T ) u(k)=10\cos(2\pi kT) u(k)=10cos(2πkT);
- 周期为 1 1 1 的方波信号 u ( k ) = 10 sign ( cos ( 2 π k T ) ) u(k)=10\operatorname{sign}(\cos(2\pi kT)) u(k)=10sign(cos(2πkT))。
采样周期取 Δ t = 0.05 \Delta t=0.05 Δt=0.05。
仿真
下面的所有仿真都使用了 simucpp。
原系统阶跃响应结果
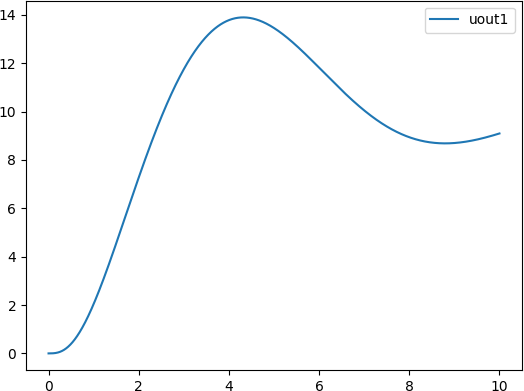
原系统阶跃响应程序
# include "simucpp.hpp"
using namespace simucpp;
using namespace zhnmat;
using namespace std;
int main() {Simulator sim1;FUInput(uin1, &sim1);FUOutput(uout1, &sim1);auto *tf1 = new TransferFcn(&sim1, vecdble{3, 4}, vecdble{1, 5, 10, 6, 4});sim1.connectU(uin1, tf1, 0);sim1.connectU(tf1, 0, uout1);uin1->Set_Function([](double t){return 10;});sim1.Initialize();sim1.Simulate(10);sim1.Plot();return 0;
}
- 阶跃信号 u ( k ) = 10 u(k)=10 u(k)=10
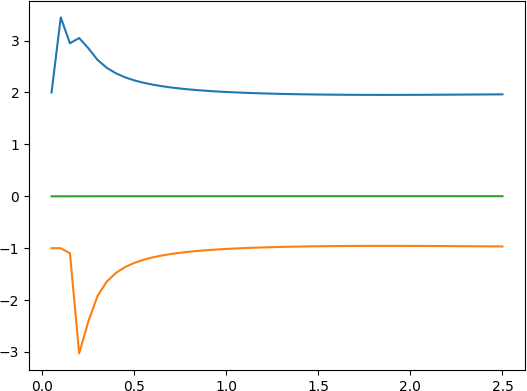
- 经 “平滑” 的阶跃信号 u ( k ) = 0.97 u ( k − 1 ) + 0.3 u(k)=0.97u(k-1)+0.3 u(k)=0.97u(k−1)+0.3
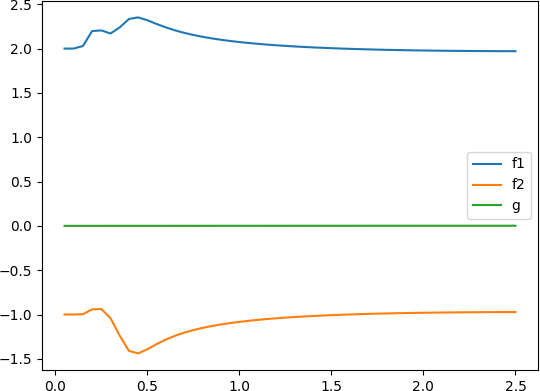
- 周期为 1 1 1 的正弦信号 u ( k ) = 10 cos ( 2 π k T ) u(k)=10\cos(2\pi kT) u(k)=10cos(2πkT)
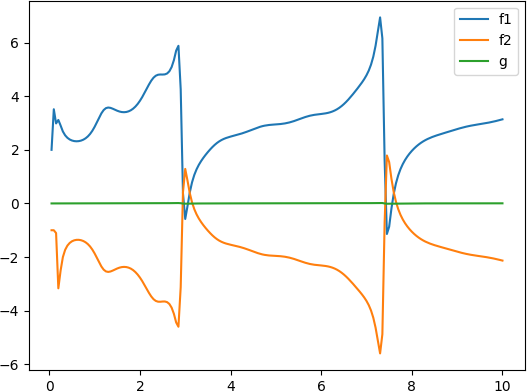
- 周期为 1 1 1 的方波信号 u ( k ) = 10 sign ( cos ( 2 π k T ) ) u(k)=10\operatorname{sign}(\cos(2\pi kT)) u(k)=10sign(cos(2πkT))
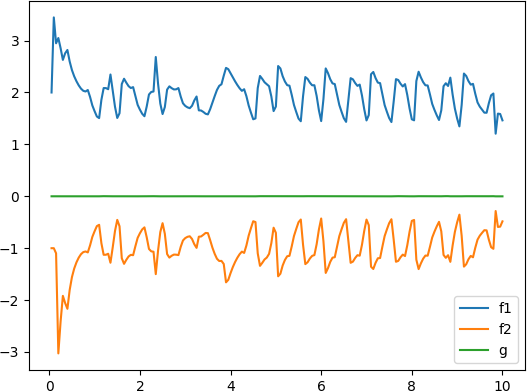
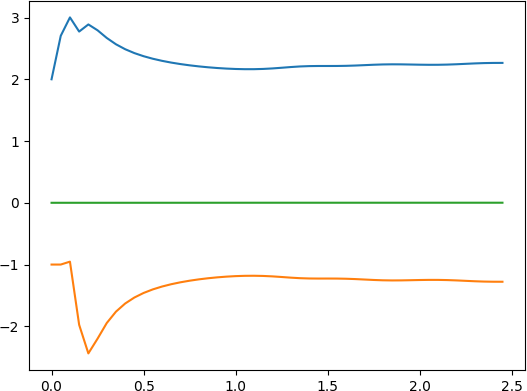
注意到最后两个正弦信号的辨识结果不准,把遗忘因子改大即可,例如改成0.99时,第3个信号的辨识结果为
代码
全部使用C++
把最小二乘法封装成一个类,主程序使用 simucpp 仿真。
/**************************************************************
// 特征模型仿真例1:参数辨识
simucpp版本:2.1.12
**************************************************************/
#include <cmath>
#include "simucpp.hpp"
#include "matplotlibcpp.h"
namespace plt = matplotlibcpp;
using namespace simucpp;
using namespace zhnmat;
using namespace std;
constexpr double LIMIT(double x, double min, double max) {return x<=min ? min : (x>=max ? max : x);}
constexpr double SIGN(double x) {return x<0 ? -1 : (x>0 ? 1 : 0);}class ParamIdentifier {
public:ParamIdentifier(double sigma=0) {_P = eye(3) * 1e6;_theta = Mat(vecdble{2, -1, 0});_lambda = 0.5;};Mat Update(double u, double y) {Mat x(vecdble{_yk1, _yk2, u});Mat K = 1/(_lambda + (x.T()*_P*x).at(0, 0)) * _P * x;_P = (eye(3) - K*x.T()) * _P / _lambda;_theta += K * (y - (x.T()*_theta).at(0, 0));_yk2 = _yk1; _yk1 = y;return _theta;}Mat _P; // P矩阵Mat _theta; // 特征模型参数(f1, f2, g)double _lambda; // 遗忘因子double _yk1=0, _yk2=0; // y(k-1)
};int main() {Simulator sim1;FUConstant(uin1, &sim1);FUOutput(uout1, &sim1);auto *tf1 = new TransferFcn(&sim1, vecdble{3, 4}, vecdble{1, 5, 10, 6, 4});ParamIdentifier idf;sim1.connectU(uin1, tf1, 0);sim1.connectU(tf1, 0, uout1);sim1.Initialize();Mat theta(3, 1);vecdble plott, plotf1, plotf2, plotg;double outValue = 0;for (uint32_t i = 0; i < 50; i++) { // 周期0.05仿真50次为2.5秒// outValue = 10;outValue = 0.97*outValue + 0.3;// outValue = 10*cos(0.1*i*M_PI);// outValue = 10*SIGN(cos(0.1*i*M_PI));uin1->Set_OutValue(outValue);for (uint32_t j = 0; j < 50; j++) // 步长0.001秒仿真50次为T=0.05秒sim1.Simulate_OneStep();theta = idf.Update(uin1->Get_OutValue(), uout1->Get_OutValue());plott.push_back(0.05*(i+1));plotf1.push_back(theta.at(0, 0));plotf2.push_back(theta.at(1, 0));plotg.push_back(theta.at(2, 0));}plt::named_plot("f1", plott, plotf1);plt::named_plot("f2", plott, plotf2);plt::named_plot("g", plott, plotg);plt::legend();plt::show();// sim1.Plot();return 0;
}
c++与python混合
被控对象使用 simucpp 并封装成动态链接库供python调用(见 Python通过SWIG调用C++),调试起来更方便。
下面为python主函数,完整代码见 https://gitee.com/xd15zhn/character_example
from plants import Plant
import numpy as np
import matplotlib.pyplot as pltplant = Plant()
plott, plotf1, plotf2, plotg = [], [], [], []
theta = np.array([[2.], [-1.], [-0.]])
P = np.eye(3)*1e6
lamb = 0.99
u = 0.
yk1, yk2 = 0, 0
for n in range(50):# u = 10.u = 0.97*u + 0.3# u = 10*np.cos(0.1*n*np.pi)# u = 10*np.sign(np.cos(0.1*n*np.pi))plant.Set_Input(u)plant.Simulate(50)y = plant.Get_Output()x = np.array([[yk1], [yk2], [u]])K = np.matmul(P, x) / (lamb + np.matmul(x.T, np.matmul(P, x)))P = 1/lamb * np.matmul((np.eye(3) - np.matmul(K, x.T)), P)theta += K*(y - np.matmul(x.T, theta))yk2, yk1 = yk1, yplott.append(n*0.05)plotf1.append(theta[0, 0])plotf2.append(theta[1, 0])plotg.append(theta[2, 0])
print('finished')
plt.plot(plott, plotf1)
plt.plot(plott, plotf2)
plt.plot(plott, plotg)
plt.show()
这篇关于特征模型仿真例1:参数辨识的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



