无人驾驶控制算法LQR和MPC的仿真实现

本文主要是介绍无人驾驶控制算法LQR和MPC的仿真实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. LQR控制器

1.1 问题陈述

考虑一个质量为 $m$ 的滑块在光滑的一维地面上运动。初始时，滑块的位置和速度均为 $0$ 。我们的目标是设计一个控制器，基于传感器测得的滑块位置 $x$ ，为滑块提供外力 $u$ ，使其能够跟随参考点 $x_r$ 运动。

在这里插入图片描述

为建立动力学模型，我们采用以下微分方程：

$\ddot x = \frac{u}{m}$

定义状态向量 $\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} =\begin{bmatrix} x \\\dot x \end{bmatrix}$ ，其中 $x_1$ 表示位移， $x_2$ 表示速度。系统的状态方程为：

$\dot x= Ax+Bu$

其中：

$A=\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix}, \quad B=\begin{bmatrix} 0 \\ \frac{1}{m} \end{bmatrix}$

系统的开环矩阵 $A$ 决定了系统是否稳定。若没有控制器，物块在光滑地面上将无法自行停止。

1.2 控制器设计

引入控制器，我们考虑以下形式：

$u=-kx=-\begin{bmatrix} k_1,k_2,\cdots \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \\ \vdots \end{bmatrix}$

从而得到新的闭环矩阵：

$\dot x = (A-Bk)x = A_{cl}x$

通过选择 $k$ ，我们可以改变 $A_{cl}$ 的特征值，从而控制系统的行为。因此，关键问题是如何选择最优的 $k$ 。

1.3 LQR控制器

引入线性二次调节器（LQR）的思想，我们定义代价函数：

$\int_0^\infty{(x^TQx+u^TRu)}dt$

其中 $Q$ 和 $R$ 是权重矩阵。通过调整权重，LQR 在保持系统稳定性的同时，寻找使代价函数最小化的控制策略。

在这里插入图片描述

1.4 仿真建模

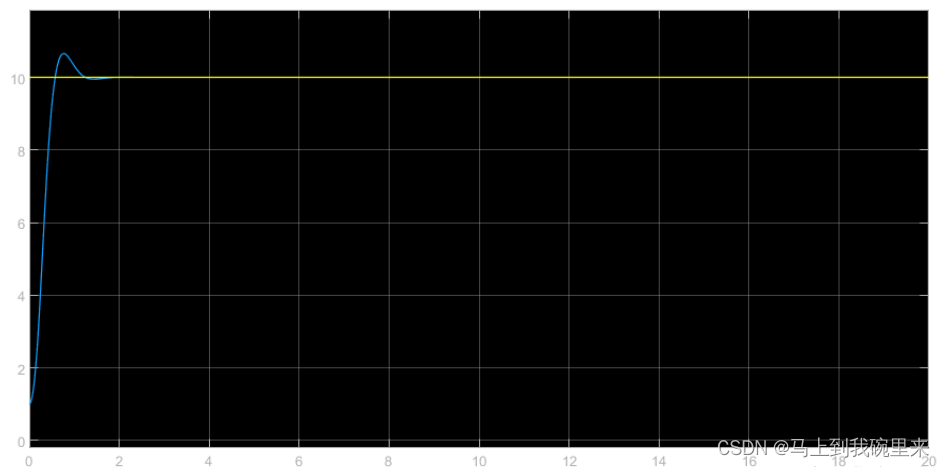
进行简单的仿真建模，通过设定初始值和目标值，LQR 控制系统能够有效地使小物块按照预设轨迹运动。

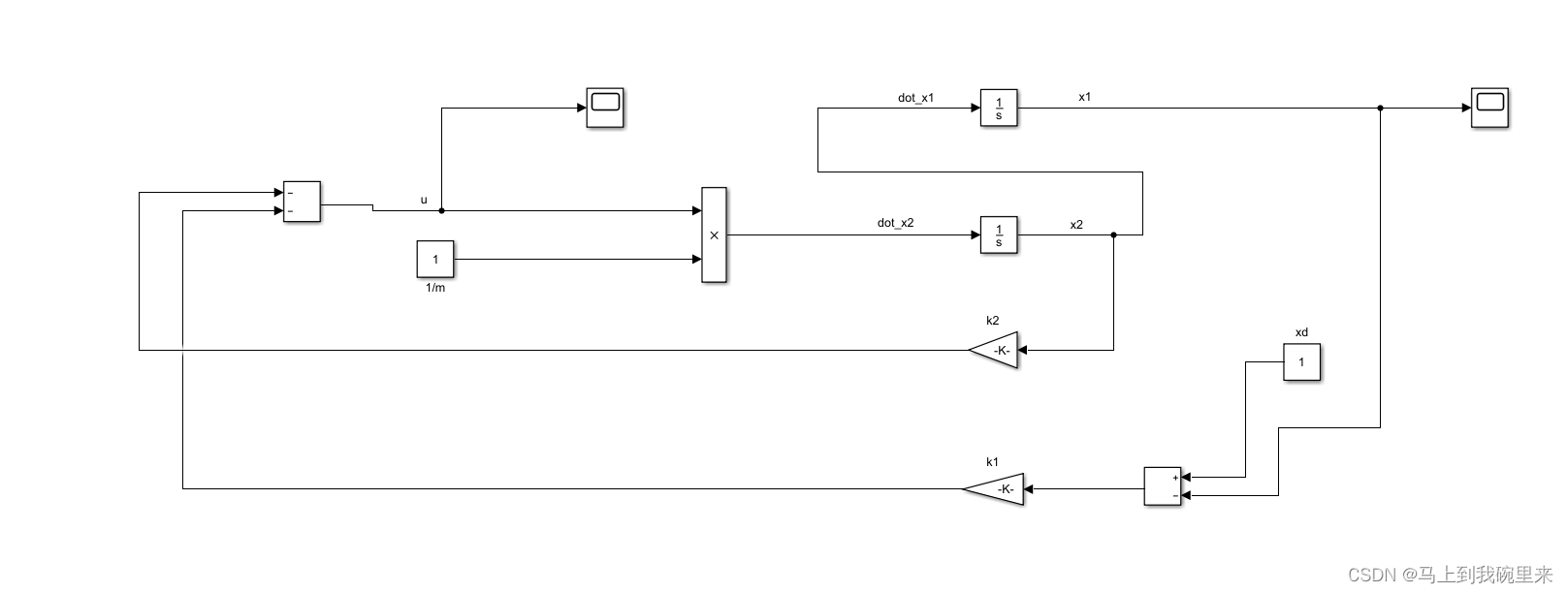
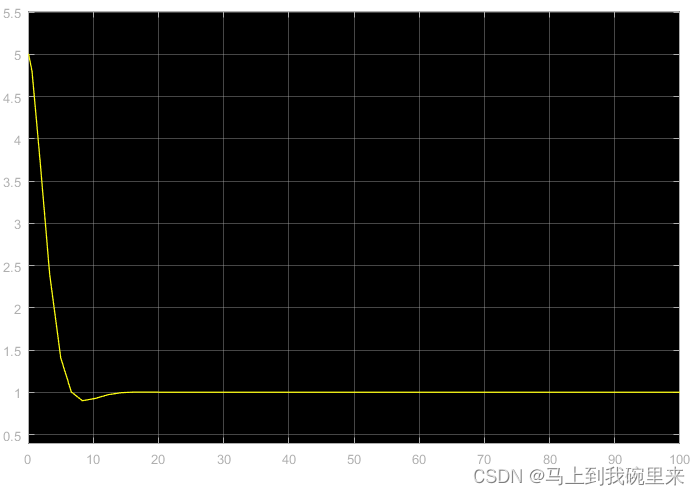
在这里插入图片描述
我们将初始值设在5，目标值设在1，最后得到

2. MPC控制器

2.1 模型的离散化

考虑同样的控制对象 $\dot x= Ax+Bu$ ，使用前向欧拉法将状态方程离散化：

$=\bar Ax(k) + \bar B u(k)$

其中

$\bar A=\begin{bmatrix} 1 & T \\ 0 & 1 \end{bmatrix},\quad \bar B=\begin{bmatrix} 0 \\ \frac{T}{m} \end{bmatrix}$

这里的 $T$ 是控制周期。

2.2 预测

MPC 的特点之一是需要对未来系统状态进行预测。在 $k$ 时刻，我们预测未来 $p$ 个控制周期内的系统状态，并定义预测时域内的控制量：

$X_k= \begin{bmatrix} x(k+1|k)^T & x(k+2|k)^T &\cdots& x(k+p|k)^T \end{bmatrix}^T$

2.3 优化

我们希望找到最佳的控制量 $U_k$ ，使预测时域内的状态向量与参考值越接近越好。这导致一个开环最优控制问题，其数学描述为：

$\min J(U_k) = U_k^T (\Theta^T Q \Theta + W) U_k +2(E^TQ\Theta) U_k +E^TQE$

其中， $\Theta$ 和 $E$ 分别为预测模型和误差。

在这里插入图片描述

2.4 仿真

对动力学方程进行拉普拉斯变换，得到传递函数 $G(s)=\frac{1}{ms^2}$ 。通过仿真，可以验证 MPC 控制系统在固定值和正弦波输入情况下能够有效跟踪目标。

$s^2X(s)=\frac{1}{m}F(s)$
得到传递函数为：
$G(s)=\frac{X(s)}{F(s)}=\frac{1}{ms^2}$
建立仿真：

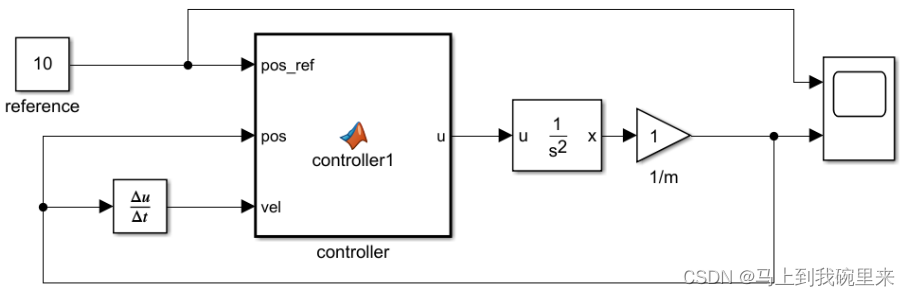
在这里插入图片描述

我们得到在固定值和sinwave的情况下基本都可以跟踪的比较好（参数还可继续优化）

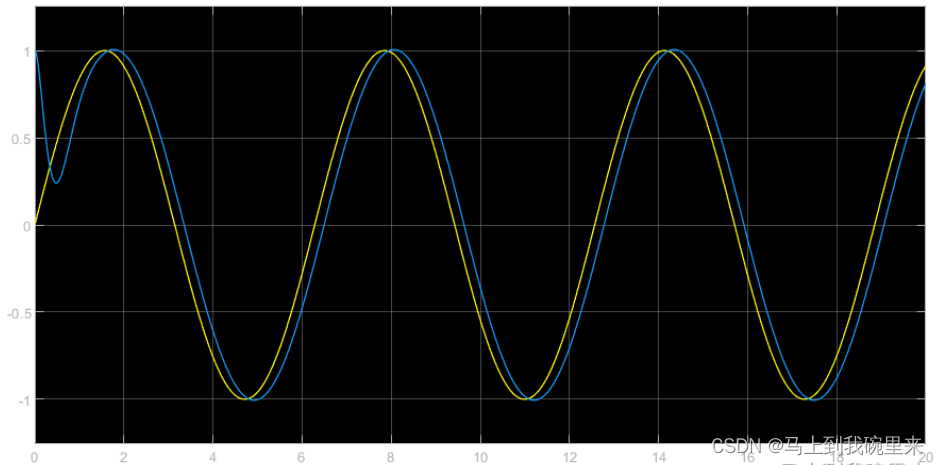
在这里插入图片描述

其中MPC代码为：

function u = Controller(pos_ref, pos, vel)
%参数设置
m    = 1.05;                %滑块质量,增加了5%作为建模误差
T    = 0.01;                %控制周期10ms
p    = 40;                  %控制时域（预测时域）
Q    = 10*eye(2*p);         %累计误差权重
W    = 0.0001*eye(p);       %控制输出权重
umax = 100;                 %控制量限制，即最大的力
Rk   = zeros(2*p,1);        %参考值序列
Rk(1:2:end) = pos_ref;    
Rk(2:2:end) = vel;          %参考速度跟随实际速度
%构建中间变量
xk    = [pos;vel];          %xk
A_    = [1 T;0 1];          %离散化预测模型参数A
B_    = [0;T/m];            %离散化预测模型参数B
psi   = zeros(2*p,2);       %psi
for i=1:1:ppsi(i*2-1:i*2,1:2)=A_^i;
end
theta = zeros(2*p,p);       %theta
for i=1:1:pfor j=1:1:itheta(i*2-1:i*2,j)=A_^(i-j)*B_;end
end
E = psi*xk-Rk;              %E
H = 2*(theta'*Q*theta+W);   %H
f = (2*E'*Q*theta)';        %f
%优化求解
coder.extrinsic('quadprog');
Uk=quadprog(H,f,[],[],[],[],-umax,umax);
%返回控制量序列第一个值
u = 0.0;                    %显示指定u的类型
u = Uk(1);