Dijkstra（迪克斯特拉）最短路径算法

本文主要是介绍Dijkstra（迪克斯特拉）最短路径算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 ,就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2、算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

3、举例分析。

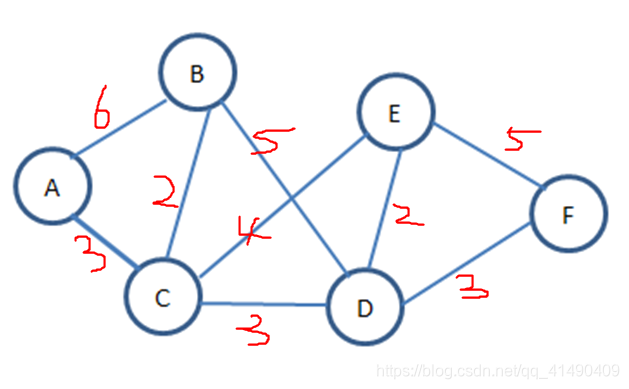
步骤

S集合

U集合

以A为源点，此时S={A}

最短路径：A $\rightarrow$ A=0

以A为中间点，从A开始找

U={B、C、D、E、F}

A $\rightarrow$ B=6

A $\rightarrow$ C=3

A $\rightarrow$ U中其它顶点= $\infty$

A $\rightarrow$ C=3最短

将C加入S中，S={A、C}

最短路径：A $\rightarrow$ A=0，A $\rightarrow$ C=3

以C为中间点，从A $\rightarrow$ C=3这条最短路径开始找

U={B、D、E、F}

A $\rightarrow$ C $\rightarrow$ B=5（比上一步的A $\rightarrow$ B=6短）

A $\rightarrow$ C $\rightarrow$ D=6

A $\rightarrow$ C $\rightarrow$ E=7

A $\rightarrow$ C $\rightarrow$ U中其它顶点= $\infty$

A $\rightarrow$ C $\rightarrow$ B=5最短

将B加入S中，S={A、C、B}

最短路径：A $\rightarrow$ A=0，A $\rightarrow$ C=3、A $\rightarrow$ C $\rightarrow$ B=5

以B为中间点，从A $\rightarrow$ C $\rightarrow$ B=5这条最短路径开始找

U={D、E、F}

A $\rightarrow$ C $\rightarrow$ B $\rightarrow$ D=10（比第二步中的A $\rightarrow$ C $\rightarrow$ D=6长，所以将D的权值更改为A $\rightarrow$ C $\rightarrow$ D=6）

A $\rightarrow$ C $\rightarrow$ B $\rightarrow$ U中其它顶点= $\infty$

A $\rightarrow$ C $\rightarrow$ D=6最短

将D加入S中，S={A、C、B、D}

最短路径：A $\rightarrow$ A=0，A $\rightarrow$ C=3、A $\rightarrow$ C $\rightarrow$ B=5、A $\rightarrow$ C $\rightarrow$ D=6

以D为中间点，从A $\rightarrow$ C $\rightarrow$ D=6这条最短路径开始找

U={E、F}

A $\rightarrow$ C $\rightarrow$ D $\rightarrow$ E=8（比第二步中的A $\rightarrow$ C $\rightarrow$ E=7长，所以将E的权值更改为A $\rightarrow$ C $\rightarrow$ E=7）

A $\rightarrow$ C $\rightarrow$ D $\rightarrow$ F=9

A $\rightarrow$ C $\rightarrow$ E=7最短

将E加入S中，S={A、C、B、D、E}

最短路径：A $\rightarrow$ A=0，A $\rightarrow$ C=3、A $\rightarrow$ C $\rightarrow$ B=5、A $\rightarrow$ C $\rightarrow$ D=6、A $\rightarrow$ C $\rightarrow$ E=7

以E为中间点，从A $\rightarrow$ C $\rightarrow$ E=7这条最短路径开始找

U={F}

A $\rightarrow$ C $\rightarrow$ E $\rightarrow$ F=12（比第四步中的A $\rightarrow$ C $\rightarrow$ D $\rightarrow$ F=9长，所以将F的权值更改为A $\rightarrow$ C $\rightarrow$ D $\rightarrow$ F=9）

A $\rightarrow$ C $\rightarrow$ D $\rightarrow$ F=9最短

将F加入S中，S={A、C、B、D、E、F}

最短路径：A $\rightarrow$ A=0，A $\rightarrow$ C=3、A $\rightarrow$ C $\rightarrow$ B=5、A $\rightarrow$ C $\rightarrow$ D=6、A $\rightarrow$ C $\rightarrow$ E=7、A $\rightarrow$ C $\rightarrow$ D $\rightarrow$ F=9

U集合为空，所有点的最短路径查找完毕。

四、matlab代码

function[dist priorVertex]=Dijkstra(w,start,terminal)
w=[0 6 3 inf inf inf;inf 0 inf 5 inf inf;inf 2 0 3 4 inf;inf inf inf 0 2 3;inf inf inf inf 0 5;inf inf inf inf inf inf];n=size(w,1);w1=w(1,:);V=1:n;%赋初值for i=1:ndist(i)=w1(i);%辅助数组dist。它的每一个分量dist[i]表示当前找到的从源点v1到顶点vi的最短路径的长度。priorVertex(i)=1;endS=[]S(1)=1;u=S(1);%更新前驱顶点k=1;while k<n%求V1到其余各顶点的最短距离%更新dist(v)和priorVertex(v)Sdiff=setdiff(V,S)%求V-S差集for i=Sdiffif dist(i)>dist(u)+w(u,i)%距离有变化的修正dist(i)=dist(u)+w(u,i);priorVertex(i)=u;endend%求v*v=Sdiff(1);m=length(Sdiff);for i=2:m;if dist(v)>dist(Sdiff(i))v=Sdiff(i);endendk=k+1;S(k)=v;%更新前驱顶点u=v;enddisp('最终V1到各个顶点的最短距离分别为:')distdisp('最终各个顶点的直接前驱分别为:')priorVertex