本文主要是介绍算法快学笔记(十八):史上最全查找算法总结,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1. 简介
查找算是工作过程中运用最广泛的操作了,操作系统读取文件时需要查找,从数据库读取数据时需要查找…
本文将对常见的查找算法进行总结。
2. 常见算法
2.1 顺序查找
基本思想:
该算法简单粗暴,从头(或是最后)开始遍历,找到要查的数据就停止遍历并返回结果,如果遍历完也没有找到就是查找不成功。
时间复杂度:O(n)
2.2 有序表
2.2.1 二分查找
基本思想:
- 将表中间位置记录的关键字与查找关键字比较,如果两者相等,则查找成功;
- 否则利用中间位置记录将表分成前、后两个子表,
- 如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,
- 否则进一步查找后一子表。
- 重复以上过程,直到找到满足条件的记录,使查找成功,或直到子表不存在为止,此时查找不成功
时间复杂度:O(log2n)
2.2.2 插值查找
对于数值变化幅度比较均匀的有序数组,要查的值在数组中的位置基本是可以确定的,例如[10,20,30,40,60,70,80,90,100,120,130,140]这个数组,30是在数组的前半部分,60应该是离30不远的位置,而130则是在数组的后半部分,120,140是在130附近。
二分查找法用在上面的数组中,对于位置的计算可能就存在优化的空间了,优化后的算法就叫插值查找法。
基本思想:基于二分查找算法,将查找点的选择改进为自适应选择,可以提高查找效率。插值查找是根据要查找的关键字key与查找表中最大最小记录的关键字比较后的查找方法,改进后的公式如下:
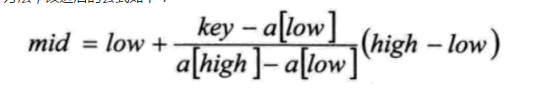
时间复杂度:o(logn)
适用场景:对于表长较大而关键字分布比较均匀的查找表来说,效率高于二分查找法。
2.2.3 斐波那契查找
斐波那契数列如下所示:
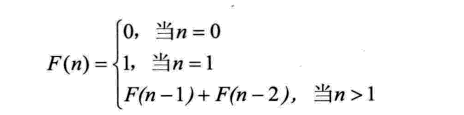
斐波那契查找原理与前两种相似,仅仅改变了中间结点(mid)的位置,mid不再是中间或插值得到,而是位于黄金分割点附近,即mid=low+F(k-1)-1(F代表斐波那契数列),如下图所示:
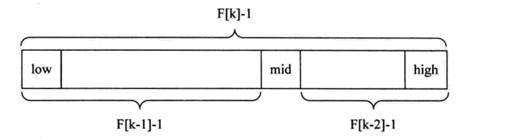
基本思想:
由斐波那契数列 F[k]=F[k-1]+F[k-2]的性质,可以得到(F[k]-1)=(F[k-1]-1)+(F[k-2]-1)+1。该式说明:只要顺序表的长度为F[k]-1,则可以将该表分成长度为F[k-1]-1和F[k-2]-1的两段,即如上图所示。从而中间位置为mid=low+F(k-1)-1
但顺序表长度n不一定刚好等于F[k]-1,所以需要将原来的顺序表长度n增加至F[k]-1。这里的k值只要能使得F[k]-1恰好大于或等于n即可。
时间复杂度:O(log2n)。
理轮上,由于下述原因,该算法的平均性能会高于二分查找法:
- 如果查找的记录在右侧,则查找的数据量会少一些
- mid=low+F(k-1)-1. 是基于加减法的操作,数据量大的时候,效率上会高于除法。
2.3 无序数据
数据按照时间存储,值可能是无序的。
2.3.1 简单索引
基本思想:存储数据的时候,使用数据的key创建出有序的索引,索引中还保存指向原始数据的指针。查找的时候可以用有序表的算法找到索引,然后用索引中存储的数据指针找到原始数据。

2.3.2 分块索引
数据量大的时候,简单索引需要较多的内存空间去存储索引数据,此时可以考虑使用分块索引。
算法思想:将n个数据元素"按块有序"划分为m块(m ≤ n)。每一块中的结点不必有序,但块与块之间必须"按块有序";即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字;而第2块中任一元素又都必须小于第3块中的任一元素,……
索引结果如下图所示:
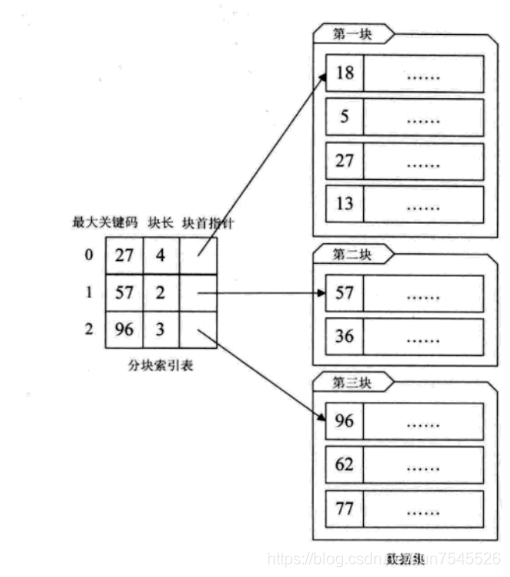
查找流程:
- 先选取各块中的最大关键字构成一个索引表;
- 查找分两个部分:先对索引表进行二分查找或顺序查找,以确定待查记录在哪一块中;然后,在已确定的块中用顺序法进行查找。
2.3.3 倒排索引
解决文本搜索的必备技能,请参考:https://blog.csdn.net/eric_sunah/article/details/79404022 第五章节
2.3.4 哈希查找
请参考:https://blog.csdn.net/eric_sunah/article/details/85393235
2.3.5 B家族的树
曾转过一篇关于常见B系列树的介绍,包括:B树、B-树、B+树、B*树,请参考:https://blog.csdn.net/eric_sunah/article/details/86482113
2.3.6 红黑树查找
请参考:https://blog.csdn.net/eric_sunah/article/details/86482146
这篇关于算法快学笔记(十八):史上最全查找算法总结的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







