C#，数值计算，矩阵的行列式（Determinant）、伴随矩阵（Adjoint）与逆矩阵（Inverse）的算法与源代码

2024-02-14 06:04
文章标签 c# 算法 计算 源代码 矩阵 .net 数值 行列式 netcore 伴随 inverse determinant adjoint

本文主要是介绍C#，数值计算，矩阵的行列式（Determinant）、伴随矩阵（Adjoint）与逆矩阵（Inverse）的算法与源代码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文发布矩阵（Matrix）的一些初级算法。

一、矩阵的行列式（Determinant）

矩阵行列式是指矩阵的全部元素构成的行列式，设A=(a)是数域P上的一个n阶矩阵，则所有A=(a)中的元素组成的行列式称为矩阵A的行列式，记为|A|或det(A)。若A，B是数域P上的两个n阶矩阵，k是P中的任一个数，则|AB|=|A||B|，|kA|=kⁿ|A|，|A*|=|A|，其中A*是A的伴随矩阵；若A是可逆矩阵，则|A|=|A|。
 

/// <summary>
/// 计算 A[p,q] 位于 [,]temp 的块辅因子
/// </summary>
/// <param name="matrix"></param>
/// <param name="temp"></param>
/// <param name="p"></param>
/// <param name="q"></param>
/// <param name="n"></param>
private static void BlockCofactor(double[,] matrix, ref double[,] temp, int p, int q, int n)
{
    int i = 0;
    int j = 0;

    for (int row = 0; row < n; row++)
    {
        for (int col = 0; col < n; col++)
        {
            if (row != p && col != q)
            {
                temp[i, j++] = matrix[row, col];
                if (j == (n - 1))
                {
                    j = 0;
                    i++;
                }
            }
        }
    }
}

/// <summary>
/// 求矩阵行列式（递归算法）
/// </summary>
/// <param name="N"></param>
/// <param name="matrix"></param>
/// <param name="n"></param>
/// <returns></returns>
public static double Determinant(int N, double[,] matrix, int n)
{
    if (n == 1)
    {
        return matrix[0, 0];
    }

    double D = 0.0;
    double[,] temp = new double[N, N];
    int sign = 1;
    for (int f = 0; f < n; f++)
    {
        BlockCofactor(matrix, ref temp, 0, f, n);
        D += sign * matrix[0, f] * Determinant(N, temp, n - 1);
        sign = -sign;
    }
    return D;
}
 

/// <summary>
/// 计算 A[p,q] 位于 [,]temp 的块辅因子
/// </summary>
/// <param name="matrix"></param>
/// <param name="temp"></param>
/// <param name="p"></param>
/// <param name="q"></param>
/// <param name="n"></param>
private static void BlockCofactor(double[,] matrix, ref double[,] temp, int p, int q, int n)
{int i = 0;int j = 0;for (int row = 0; row < n; row++){for (int col = 0; col < n; col++){if (row != p && col != q){temp[i, j++] = matrix[row, col];if (j == (n - 1)){j = 0;i++;}}}}
}/// <summary>
/// 求矩阵行列式（递归算法）
/// </summary>
/// <param name="N"></param>
/// <param name="matrix"></param>
/// <param name="n"></param>
/// <returns></returns>
public static double Determinant(int N, double[,] matrix, int n)
{if (n == 1){return matrix[0, 0];}double D = 0.0;double[,] temp = new double[N, N];int sign = 1;for (int f = 0; f < n; f++){BlockCofactor(matrix, ref temp, 0, f, n);D += sign * matrix[0, f] * Determinant(N, temp, n - 1);sign = -sign;}return D;
}

二、矩阵的伴随矩阵（Adjoint Matrix）

一个方形矩阵的伴随矩阵是一个类似于逆矩阵的概念。如果二维矩阵可逆，那么它的逆矩阵和它的伴随矩阵之间只差一个系数，对多维矩阵也存在这个规律。然而，伴随矩阵对不可逆的矩阵也有定义，并且不需要用到除法。
 

/// <summary>
/// 伴随矩阵
/// </summary>
/// <param name="A"></param>
/// <param name="adj"></param>
public static void Adjoint(double[,] matrix, out double[,] adjoint)
{
    int N = matrix.GetLength(0);
    adjoint = new double[N, N];

    if (N == 1)
    {
        adjoint[0, 0] = 1.0;
        return;
    }

    int sign = 1;
    double[,] temp = new double[N, N];
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            BlockCofactor(matrix, ref temp, i, j, N);
            sign = ((i + j) % 2 == 0) ? 1 : -1;
            adjoint[j, i] = (sign) * (Determinant(N, temp, N - 1));
        }
    }
}

/// <summary>
/// 伴随矩阵
/// </summary>
/// <param name="A"></param>
/// <param name="adj"></param>
public static void Adjoint(double[,] matrix, out double[,] adjoint)
{int N = matrix.GetLength(0);adjoint = new double[N, N];if (N == 1){adjoint[0, 0] = 1.0;return;}int sign = 1;double[,] temp = new double[N, N];for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){BlockCofactor(matrix, ref temp, i, j, N);sign = ((i + j) % 2 == 0) ? 1 : -1;adjoint[j, i] = (sign) * (Determinant(N, temp, N - 1));}}
}

三、矩阵的逆矩阵（Inverse Matrix）

设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E ，则称方阵A可逆，并称方阵B是A的逆矩阵。矩阵求逆，即求矩阵的逆矩阵。矩阵是线性代数的主要内容，很多实际问题用矩阵的思想去解既简单又快捷。逆矩阵又是矩阵理论的很重要的内容，逆矩阵的求法自然也就成为线性代数研究的主要内容之一。

/// <summary>
/// 矩阵求逆
/// </summary>
/// <param name="A"></param>
/// <param name="inverse"></param>
/// <returns></returns>
public static bool Inverse(double[,] matrix, out double[,] inverse)
{
    int N = matrix.GetLength(0);
    inverse = new double[N, N];

    double det = Determinant(N, matrix, N);
    if (det == 0)
    {
        return false;
    }

    Adjoint(matrix, out double[,] adj);

    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        {
            inverse[i, j] = adj[i, j] / (double)det;
        }
    }
    return true;
}
 

/// <summary>
/// 矩阵求逆
/// </summary>
/// <param name="A"></param>
/// <param name="inverse"></param>
/// <returns></returns>
public static bool Inverse(double[,] matrix, out double[,] inverse)
{int N = matrix.GetLength(0);inverse = new double[N, N];double det = Determinant(N, matrix, N);if (det == 0){return false;}Adjoint(matrix, out double[,] adj);for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){inverse[i, j] = adj[i, j] / (double)det;}}return true;
}

演算代码：

private void button1_Click(object sender, EventArgs e)
{
    double[,] A = { 
        {5, -2, 2, 7},
        {1, 0, 0, 3},
        {-3, 1, 5, 0},
        {3, -1, -9, 4}
    };

    double d = Algorithm_Gallery.Determinant(4, A, 4);

    StringBuilder sb = new StringBuilder();
    sb.Append(Welcome());
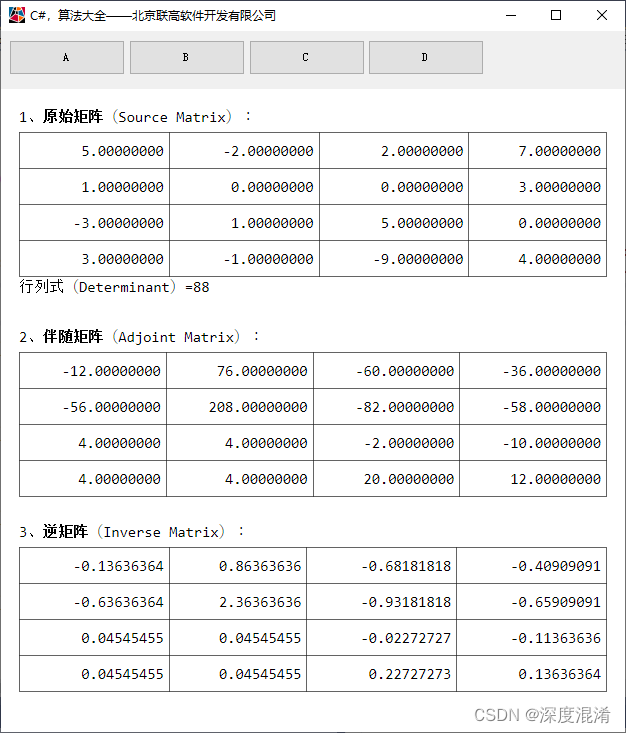
    sb.AppendLine("1、<b>原始矩阵</b>（Source Matrix）：<br>");
    sb.Append(Algorithm_Gallery.ToHtml(A));
    sb.AppendLine("行列式（Determinant）=" + d + "<br>");
    
    Algorithm_Gallery.Adjoint(A, out double[,] adj);
    sb.AppendLine("<br>2、<b>伴随矩阵</b>（Adjoint Matrix）：<br>");
    sb.Append(Algorithm_Gallery.ToHtml(adj));
    
    Algorithm_Gallery.Inverse(A, out double[,] inv);
    sb.AppendLine("<br>3、<b>逆矩阵</b>（Inverse Matrix）：<br>");
    sb.Append(Algorithm_Gallery.ToHtml(inv));
    sb.Append(Bye());
    webBrowser1.DocumentText = sb.ToString();
}

private void button1_Click(object sender, EventArgs e)
{double[,] A = { {5, -2, 2, 7},{1, 0, 0, 3},{-3, 1, 5, 0},{3, -1, -9, 4}};double d = Algorithm_Gallery.Determinant(4, A, 4);StringBuilder sb = new StringBuilder();sb.Append(Welcome());sb.AppendLine("1、<b>原始矩阵</b>（Source Matrix）：<br>");sb.Append(Algorithm_Gallery.ToHtml(A));sb.AppendLine("行列式（Determinant）=" + d + "<br>");Algorithm_Gallery.Adjoint(A, out double[,] adj);sb.AppendLine("<br>2、<b>伴随矩阵</b>（Adjoint Matrix）：<br>");sb.Append(Algorithm_Gallery.ToHtml(adj));Algorithm_Gallery.Inverse(A, out double[,] inv);sb.AppendLine("<br>3、<b>逆矩阵</b>（Inverse Matrix）：<br>");sb.Append(Algorithm_Gallery.ToHtml(inv));sb.Append(Bye());webBrowser1.DocumentText = sb.ToString();
}

 打印矩阵的代码：


public static string ToHtml(double[,] y)
{
    int m = y.GetLength(0);
    int n = y.GetLength(1);
    StringBuilder sb = new StringBuilder();
    sb.AppendLine("<style>");
    sb.AppendLine("td { padding:5px;text-align:right; }");
    sb.AppendLine("</style>");
    sb.AppendLine("<table width='100%' border=1 bordercolor='#999999' style='border-collapse:collapse;'>");
    for (int i = 0; i < m; i++)
    {
        sb.AppendLine("<tr>");
        for (int j = 0; j < n; j++)
        {
            sb.AppendLine("<td>" + String.Format("{0:F8}", y[i, j]) + "</td>");
        }
        sb.AppendLine("</tr>");
    }
    sb.AppendLine("</table>");
    return sb.ToString();
}
 

————————————————————————————————

POWER BY  TRUFFER.CN 50018.COM 315SOFT.COM

public static string ToHtml(double[,] y)
{int m = y.GetLength(0);int n = y.GetLength(1);StringBuilder sb = new StringBuilder();sb.AppendLine("<style>");sb.AppendLine("td { padding:5px;text-align:right; }");sb.AppendLine("</style>");sb.AppendLine("<table width='100%' border=1 bordercolor='#999999' style='border-collapse:collapse;'>");for (int i = 0; i < m; i++){sb.AppendLine("<tr>");for (int j = 0; j < n; j++){sb.AppendLine("<td>" + String.Format("{0:F8}", y[i, j]) + "</td>");}sb.AppendLine("</tr>");}sb.AppendLine("</table>");return sb.ToString();
}

这篇关于C#，数值计算，矩阵的行列式（Determinant）、伴随矩阵（Adjoint）与逆矩阵（Inverse）的算法与源代码的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/707687。

相关文章

C#中lock关键字的使用小结

C#中lock关键字的使用小结

《C#中lock关键字的使用小结》在C#中,lock关键字用于确保当一个线程位于给定实例的代码块中时,其他线程无法访问同一实例的该代码块,下面就来介绍一下lock关键字的使用... 目录使用方式工作原理注意事项示例代码为什么不能lock值类型在C#中，lock关键字用于确保当一个线程位于给定实例的代码块中时
阅读更多...
C# $字符串插值的使用

C# $字符串插值的使用

《C#$字符串插值的使用》本文介绍了C#中的字符串插值功能,详细介绍了使用$符号的实现方式,文中通过示例代码介绍的非常详细,需要的朋友们下面随着小编来一起学习学习吧... 目录$ 字符使用方式创建内插字符串包含不同的数据类型控制内插表达式的格式控制内插表达式的对齐方式内插表达式中使用转义序列内插表达式中使用
阅读更多...
C#中的Converter的具体应用

C#中的Converter的具体应用

《C#中的Converter的具体应用》C#中的Converter提供了一种灵活的类型转换机制,本文详细介绍了Converter的基本概念、使用场景,具有一定的参考价值,感兴趣的可以了解一下... 目录Converter的基本概念1. Converter委托2. 使用场景布尔型转换示例示例1：简单的字符串到
阅读更多...
C#监听txt文档获取新数据方式

C#监听txt文档获取新数据方式

《C#监听txt文档获取新数据方式》文章介绍通过监听txt文件获取最新数据,并实现开机自启动、禁用窗口关闭按钮、阻止Ctrl+C中断及防止程序退出等功能,代码整合于主函数中,供参考学习... 目录前言一、监听txt文档增加数据二、其他功能1. 设置开机自启动2. 禁止控制台窗口关闭按钮3. 阻止Ctrl +
阅读更多...
C#解析JSON数据全攻略指南

C#解析JSON数据全攻略指南

《C#解析JSON数据全攻略指南》这篇文章主要为大家详细介绍了使用C#解析JSON数据全攻略指南,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录一、为什么jsON是C#开发必修课？二、四步搞定网络JSON数据1. 获取数据 - HttpClient最佳实践2. 动态解析 - 快速
阅读更多...
C#连接SQL server数据库命令的基本步骤

C#连接SQL server数据库命令的基本步骤

《C#连接SQLserver数据库命令的基本步骤》文章讲解了连接SQLServer数据库的步骤,包括引入命名空间、构建连接字符串、使用SqlConnection和SqlCommand执行SQL操作,... 目录建议配合使用：如何下载和安装SQL server数据库-CSDN博客1. 引入必要的命名空间2.
阅读更多...
C#读写文本文件的多种方式详解

C#读写文本文件的多种方式详解

《C#读写文本文件的多种方式详解》这篇文章主要为大家详细介绍了C#中各种常用的文件读写方式,包括文本文件,二进制文件、CSV文件、JSON文件等,有需要的小伙伴可以参考一下... 目录一、文本文件读写1. 使用 File 类的静态方法2. 使用 StreamReader 和 StreamWriter二、二进
阅读更多...
C#中Guid类使用小结

C#中Guid类使用小结

《C#中Guid类使用小结》本文主要介绍了C#中Guid类用于生成和操作128位的唯一标识符,用于数据库主键及分布式系统,支持通过NewGuid、Parse等方法生成,感兴趣的可以了解一下... 目录前言一、什么是 Guid二、生成 Guid1. 使用 Guid.NewGuid() 方法2. 从字符串创建
阅读更多...
C# 比较两个list 之间元素差异的常用方法

C# 比较两个list 之间元素差异的常用方法

《C#比较两个list之间元素差异的常用方法》：本文主要介绍C#比较两个list之间元素差异,本文通过实例代码给大家介绍的非常详细,对大家的学习或工作具有一定的参考借鉴价值,需要的朋友参考下吧... 目录1. 使用Except方法2. 使用Except的逆操作3. 使用LINQ的Join,GroupJoin
阅读更多...
Java中的雪花算法Snowflake解析与实践技巧

Java中的雪花算法Snowflake解析与实践技巧

《Java中的雪花算法Snowflake解析与实践技巧》本文解析了雪花算法的原理、Java实现及生产实践,涵盖ID结构、位运算技巧、时钟回拨处理、WorkerId分配等关键点,并探讨了百度UidGen... 目录一、雪花算法核心原理1.1 算法起源1.2 ID结构详解1.3 核心特性二、Java实现解析2.
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2