本文主要是介绍代码随想录算法训练营Day56|583. 两个字符串的删除操作、72. 编辑距离,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
583. 两个字符串的删除操作
前言
思路
算法实现
法二
72. 编辑距离
前言
思路
算法实现
总结
583. 两个字符串的删除操作
题目链接
文章链接
前言
本题与上一题不同的子序列相比,变化就是两个字符串都可以进行删除操作了。
思路
利用动规五部曲进行分析:
1.确定dp数组及其下标的含义:
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
2.确定递推公式:
递推公式的推导与前几题大致类似,都有分两种情况进行讨论:
- 当word1[i - 1] 与 word2[j - 1]相同的时候;
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
对于word1[i - 1] 与 word2[j - 1]相同时,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1,
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1,
情况三,同时删word1[i - 1]和word2[j - 1], 操作的最少次数为dp[i - 1][j - 1] + 2;
最终结果是取三种情况的最小值,dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});
3.初始化dp数组:
从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。
当word2为空字符串时,word1字符串的长度为i,因此要删i次才能与空字符串word2相等,所以dp[i][0]的初值为i,同理dp[0][j]的初值为j;
4.确定遍历顺序:
从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。
所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
5.打印dp数组:
以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
算法实现
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int> (word2.size() + 1, 0));for (int i = 1; i <= word1.size(); i++) dp[i][0] = i;for (int j = 1; j <= word2.size(); j++) dp[0][j] = j;for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];else {dp[i][j] = min(dp[i - 1][j] + 1, min(dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2));}}}return dp[word1.size()][word2.size()];}
};法二
利用求最长公共子序列的思想,两个字符串要删除的部分就是最长公共子序列之外的部分。
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int> (word2.size() + 1, 0));for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}return word1.size() + word2.size() - dp[word1.size()][word2.size()] * 2;}
};72. 编辑距离
题目链接
文章链接
前言
前几题都是为了本题做铺垫,有了前面几题的学习接触本题就不会觉得非常困难,主要难点还是在于递推公式的确定,尤其是当两个字符串比较的位置字符不相等时递推公式的确定。
思路
还是利用动规五部曲进行分析:
1.确定dp数组及其下标的含义:
dp[i][j]:以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
2.确定递推公式:
依然是分两种大情况进行讨论:
- 当word1[i - 1] 与 word2[j - 1]相同;
- 当word1[i - 1] 与 word2[j - 1]不相同;
当word1[i - 1] 与 word2[j - 1]相同时,不需要进行额外的操作(编辑距离),和word1以i - 2为结尾,word2以就j - 2为结尾要操作的次数一样,即dp[i][j] = dp[i - 1][j - 1];
而当word1[i - 1] 与 word2[j - 1]不相同时,要分别考虑删、增、换三种不同的情况;
增删元素其实本质上是一样的,在word1中增加元素和在word2中删除元素起到的效果相同,此时dp[i][j] = dp[i - 1][j] + 1(删word1中的元素),或者dp[i][j] = dp[i][j - 1] + 1(删除word2中的元素);
替换元素时,替换word[i - 1]元素使其与word2[j - 1]相等(也可以倒过来),此时dp[i][j] = dp[i - 1][j - 1] + 1;
3.dp数组初始化
与上题一样dp[i][0] = i,dp[0][j] = j,只需要删除完所有字符就能与另一个空字符串相等;
4.确定遍历顺序:
从递推公式可以看出,dp[i][j]是依赖左方,上方和左上方元素的,如图:
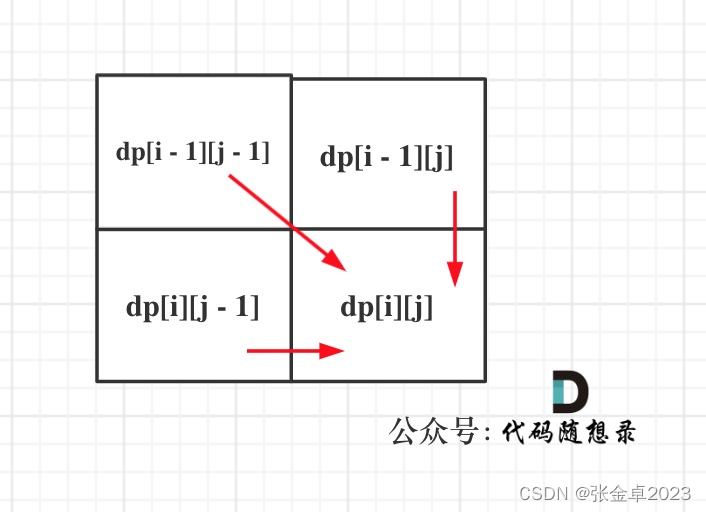
5.打印dp数组:
以示例1为例,输入:word1 = "horse", word2 = "ros"为例,dp矩阵状态图如下:
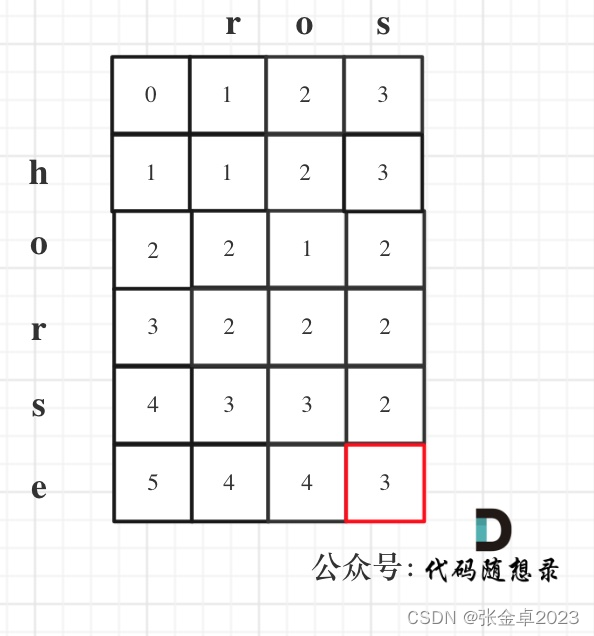
算法实现
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>> dp(word1.size() + 1, vector<int> (word2.size() + 1, 0));for (int i = 1; i <= word1.size(); i++) dp[i][0] = i;for (int j = 1; j <= word2.size(); j++) dp[0][j] = j;for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];else dp[i][j] = min(dp[i - 1][j] + 1, min(dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1));}}return dp[word1.size()][word2.size()];}
};总结
今天的两道题是前面几道题的深化,循序渐进。
这篇关于代码随想录算法训练营Day56|583. 两个字符串的删除操作、72. 编辑距离的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





