[树] △ 由广义表GList创建树（孩子兄弟链表CSTree）（严蔚敏《数据结构》6.73）

2024-02-13 12:18
文章标签 链表 数据结构 创建 孩子 广义 兄弟 严蔚敏 cstree glist 6.73

本文主要是介绍[树] △ 由广义表GList创建树（孩子兄弟链表CSTree）（严蔚敏《数据结构》6.73），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目来源：严蔚敏《数据结构》C语言版本习题册 6.73

【题目】6.73
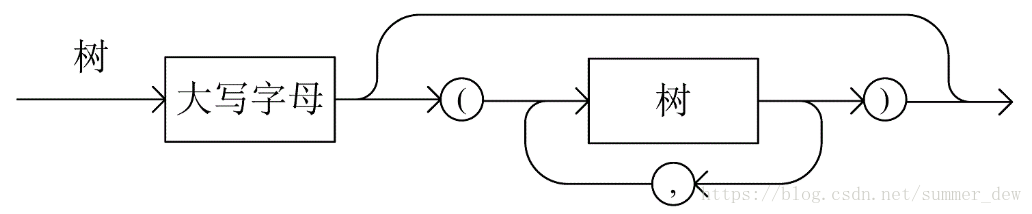
若用大写字母标识树的结点，则可用带标号的广义表形式表示一棵树，其语法图如下所示：

在这里插入图片描述

例如，6.71题中的树可用下列形式的广义表表示：A(B(E,F),C(G),D)
试写一递归算法，由这种广义表表示的字符序列构造树的孩子-兄弟链表（提示：按照森林和树相互递归的定义写两个互相递归调用的算法，语法图中一对圆括号内的部分可看成为森林的语法图）。

【如何看语法图】https://blog.csdn.net/summer_dew/article/details/82937736
【公式解析】

按照公式有 [树] 的定义：

  1. 不存在空树
  2. 树根：大写字母
    • 没有子树：空
    • 有子树：( 树 ) --> 树里面又返回树的定义
    • 有多个子树：(树1, 树2, 树...) --> 以,分割

【测试数据】

A(B(E,F),C(G),D)
A
A(B)
A(B,C)
A(B,C(D,E))

【答案】

/*-----------------------------------------|6.73 用广义表的形式构造                 |-----------------------------------------*/
// @Version:1.0.1
// @Time:20181005
// @Desc:改进v0.0.1中的循环条件1，加上判断格式
// @Quesion:有一些格式检测不了"A(" "A()" "A)("
Status CreateCSTreeByGList(CSTree *pT) {char c;//创建新结点*pTfor (c=getchar(); c!='\n'; c=getchar()) {if (c>='A' && c<='Z') { //新结点的信息*pT = (CSNode *)malloc(sizeof(CSNode)); if (!*pT) exit(OVERFLOW);(*pT)->data = c; (*pT)->firstchild=(*pT)->nextsibling=NULL;} else if (c=='(') { //新结点的孩子if ( !CreateCSTreeByGList(&(*pT)->firstchild) ) return ERROR; //返回ERROR，表示此层之后发生了错误} else if (c==',') { //新结点的兄弟if ( !CreateCSTreeByGList(&(*pT)->nextsibling) ) return ERROR; //返回ERROR，表示此层之后发生了错误return OK; //新结点已经构造完了-->这里要返回} else if (c==')') { //新结点的父亲已经构建完了return OK;} else {return ERROR; //格式错误}}return TRUE; //正常结束
}

【完整答案】可以直接运行

/*-------------------|树-孩子兄弟表达法 |-------------------*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>#ifndef BASE
#define BASE
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
typedef int bool;
#endif#define TElemType char
void visit(TElemType e) {printf("%c", e);
}
typedef struct CSNode{TElemType data;struct CSNode *firstchild, *nextsibling;
}CSNode, *CSTree;/*-------------------|6.59 输出T的所有边 |-------------------*/
void TreePrintEdge(CSTree T) {CSNode *p;for (p=T->firstchild; p; p=p->nextsibling) {printf("(%c,%c)\n", T->data, p->data); //输出T的孩子TreePrintEdge(p); //输出p的孩子}
}/*-------------------------|6.60 统计叶子结点的个数 |-------------------------*/
int TreeLeafCnt(CSTree T) {// 树的叶子结点-->没有孩子int ret=0;CSNode *p;if (!T) return 0;else if (!T->firstchild) return 1;else {for (p=T->firstchild; p; p=p->nextsibling) ret += TreeLeafCnt(p);return ret;}
}/*-------------------------|6.61 求树的度           |-------------------------*/
int TreeDegree(CSTree T) {// 最大的孩子数int max=-1;int cnt=0;CSNode *child;if (!T) return -1; //空树else if (!T->firstchild) return 0; //只有一个根结点，度为0else {for (cnt=0,child=T->firstchild; child; child=child->nextsibling) cnt++; //求自己的度max = cnt; //当前的最大值for (child=T->firstchild; child; child=child->nextsibling) {cnt = TreeDegree(child);if (cnt>max) max=cnt;}return max;}
}/*-------------------------|6.62 求树的深度         |-------------------------*/
int TreeDepth(CSTree T) {int h1,h2;if (!T) return 0;else {h1 = TreeDepth(T->firstchild)+1; //T孩子的深度+1h2 = TreeDepth(T->nextsibling); //T兄弟的深度return h1>h2 ? h1 : h2;}
}/*---------------------------------|6.66 双亲表示法-->孩子兄弟表达式|---------------------------------*/
#define MAX_TREE_SIZE 50typedef struct PTNode{TElemType data;int parent; //双亲的位置域
}PTNode;
typedef struct{PTNode nodes[MAX_TREE_SIZE];int r,n;
}PTree;
CSTree CreateCSTreeByPTree(PTree T) {CSNode *tmp[MAX_TREE_SIZE]; //创建一个辅助的数组，仿照PTree结点的位置存放CSNode *p, *q;int i,parent;if (T.n<=0) return NULL;for (i=0; i<T.n; i++) { //双亲表按层序存储//创建新结点p = (CSNode *)malloc(sizeof(CSNode)); if(!p) exit(OVERFLOW);//赋值p->data = T.nodes[i].data;p->firstchild=p->nextsibling=NULL;//连接parent=T.nodes[i].parent; //父亲if (parent!=-1) { //不是根结点if (tmp[parent]->firstchild==NULL) tmp[parent]->firstchild=p; //第一个孩子else { //不是第一个孩子for (q=tmp[parent]->firstchild; q->nextsibling; q=q->nextsibling) ; //找到最后一个孩子q->nextsibling = p; //连接}}tmp[i]=p;}return tmp[0];
}/*---------------------------------|6.67 二元组(F,C)创建CSTree      |---------------------------------*/
#define maxSize 50
Status CreateCSTreeByDuplet(CSTree *pT) {char input[5];CSNode *queue[maxSize];int front,rear;CSNode *p, *q;front=rear=0; //对队列初始化for (scanf("%s", input); input[1]!='^'; scanf("%s", input)) {//创建结点p = (CSNode *)malloc(sizeof(CSNode)); if (!p) exit(OVERFLOW);p->data=input[1];p->firstchild=p->nextsibling=NULL;//入队列queue[rear]=p;rear=(rear+1)%maxSize;//找爸爸if (input[0]=='^') { //根结点-->不需要找爸爸*pT = p; //传出去} else {for (q=queue[front]; q->data!=input[0]; front=(front+1)%maxSize,q=queue[front]) ; //找爸爸//找哥哥if (!q->firstchild) q->firstchild=p; //它是最大的else { //它不是最大的for(q=q->firstchild; q->nextsibling; q=q->nextsibling) ; //找最近的哥哥q->nextsibling = p; //和哥哥牵手}}}return OK;
}/*-----------------------------------------|6.68 层次序列+每个结点的度-->构造CSTree |-----------------------------------------*/
CSTree CreateCSTreeByLevelDegree(char *levelstr, int *num) {int cnt,i,parent;CSNode *p;CSNode *tmp[maxSize];//先创建结点for (i=0; i < strlen(levelstr); ++i) {p = (CSNode *)malloc(sizeof(CSNode)); if (!p) exit(OVERFLOW);p->data = levelstr[i];p->firstchild=p->nextsibling=NULL;tmp[i]=p;}//连接parent=0; //孩子的爸爸cnt=0; //计数器：表示已经找了几个孩子i=1; //遍历结点，为他们找爸爸while (i<strlen(levelstr)) {if (num[parent]==0 || cnt==num[parent]) { //这个父亲没有孩子 || parent的孩子已经找完了cnt=0; //计数器归0parent++; //位移一位continue;}//这个父亲有孩子（i是parent的孩子）cnt++;if (cnt==1) { //i是parent的第一个孩子tmp[parent]->firstchild = tmp[i];} else { //不是第一个孩子tmp[i-1]->nextsibling = tmp[i]; //它是前面的兄弟}i++;}return tmp[0];
}/*-----------------------------------------|6.71 以树状的形式输出                   |-----------------------------------------*/
void PrintAsTree(CSTree T,int i) {/*思路：1. 观察题目输出的序列ABEFCGD2. 此为树的先根遍历-->对应为二叉树存储的先序遍历3. 前面的空格是该结点所在的层数*/int cnt;if (T) {//输出空格for (cnt=1; cnt<i; cnt++) printf(" ");//输出字符visit(T->data);printf("\n");PrintAsTree(T->firstchild, i+1);PrintAsTree(T->nextsibling, i);}
}/*-----------------------------------------|6.73 用广义表的形式构造                 |-----------------------------------------*/
// @Version:0.0.1
// @Time:20181005
// @Desc:循环条件为1，最好不要设置死循环
Status CreateCSTreeByGList1(CSTree *pT) {char c;while (1) {c = getchar();if (c>='A' && c<='Z') { //根结点*pT = (CSNode *)malloc(sizeof(CSNode)); if (!*pT) exit(OVERFLOW);(*pT)->data = c; (*pT)->firstchild=(*pT)->nextsibling=NULL;} else if (c=='(') { //是我的第一个孩子CreateCSTreeByGList1(&(*pT)->firstchild);} else if (c==',') { //是我的兄弟CreateCSTreeByGList1(&(*pT)->nextsibling);break; //这里要返回} elsebreak;}return OK;
}
// @Version:1.0.1
// @Time:20181005
// @Desc:改进v0.0.1中的循环条件1，加上判断格式
// @Quesion:有一些格式检测不了"A(" "A()" "A)("
Status CreateCSTreeByGList(CSTree *pT) {char c;//创建新结点*pTfor (c=getchar(); c!='\n'; c=getchar()) {if (c>='A' && c<='Z') { //新结点的信息*pT = (CSNode *)malloc(sizeof(CSNode)); if (!*pT) exit(OVERFLOW);(*pT)->data = c; (*pT)->firstchild=(*pT)->nextsibling=NULL;} else if (c=='(') { //新结点的孩子if ( !CreateCSTreeByGList(&(*pT)->firstchild) ) return ERROR; //返回ERROR，表示此层之后发生了错误} else if (c==',') { //新结点的兄弟if ( !CreateCSTreeByGList(&(*pT)->nextsibling) ) return ERROR; //返回ERROR，表示此层之后发生了错误return OK; //新结点已经构造完了-->这里要返回} else if (c==')') { //新结点的父亲已经构建完了return OK;} else {return ERROR; //格式错误}}return TRUE; //正常结束
}/*-----------------------------------------|6.74 以广义表的形式输出                 |-----------------------------------------*/
void PrintAsGList(CSTree T) {CSNode *child;visit(T->data);if (T->firstchild) { //有孩子printf("(");for (child=T->firstchild; child->nextsibling; child=child->nextsibling) {PrintAsGList(child);printf(",");}PrintAsGList(child);printf(")");}
}int main() {
/*6.74测试数据
A(B(E,F),C(G),D)
A
A(B)
A(B,C)
A(B,C(D,E))
*/CSTree CST;int ret;while (1) {ret = CreateCSTreeByGList(&CST); //6.73if (ret) {PrintAsGList(CST); //6.74printf("\n");}elseprintf("格式错误\n");}return 0;
}

这篇关于[树] △ 由广义表GList创建树（孩子兄弟链表CSTree）（严蔚敏《数据结构》6.73）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/705509。

相关文章

Spring创建Bean的八种主要方式详解

Spring创建Bean的八种主要方式详解

《Spring创建Bean的八种主要方式详解》Spring（尤其是SpringBoot）提供了多种方式来让容器创建和管理Bean,@Component、@Configuration+@Bean、@En... 目录引言一、Spring 创建 Bean 的 8 种主要方式1. @Component 及其衍生注解
阅读更多...
redis数据结构之String详解

redis数据结构之String详解

《redis数据结构之String详解》Redis以String为基础类型,因C字符串效率低、非二进制安全等问题,采用SDS动态字符串实现高效存储,通过RedisObject封装,支持多种编码方式（如... 目录一、为什么Redis选String作为基础类型？二、SDS底层数据结构三、RedisObject
阅读更多...
MySQL 数据库表操作完全指南:创建、读取、更新与删除实战

MySQL 数据库表操作完全指南:创建、读取、更新与删除实战

《MySQL数据库表操作完全指南:创建、读取、更新与删除实战》本文系统讲解MySQL表的增删查改（CURD）操作,涵盖创建、更新、查询、删除及插入查询结果,也是贯穿各类项目开发全流程的基础数据交互原... 目录mysql系列前言一、Create(创建)并插入数据1.1 单行数据 + 全列插入1.2 多行数据
阅读更多...
Java集合中的链表与结构详解

Java集合中的链表与结构详解

《Java集合中的链表与结构详解》链表是一种物理存储结构上非连续的存储结构,数据元素的逻辑顺序的通过链表中的引用链接次序实现,文章对比ArrayList与LinkedList的结构差异,详细讲解了链表... 目录一、链表概念与结构二、当向单链表的实现2.1 准备工作2.2 初始化链表2.3 打印数据、链表长
阅读更多...
MySQL 临时表创建与使用详细说明

MySQL 临时表创建与使用详细说明

《MySQL临时表创建与使用详细说明》MySQL临时表是存储在内存或磁盘的临时数据表,会话结束时自动销毁,适合存储中间计算结果或临时数据集,其名称以#开头（如#TempTable）,本文给大家介绍M... 目录mysql 临时表详细说明1.定义2.核心特性3.创建与使用4.典型应用场景5.生命周期管理6.注
阅读更多...
MySQL的触发器全解析(创建、查看触发器)

MySQL的触发器全解析(创建、查看触发器)

《MySQL的触发器全解析(创建、查看触发器)》MySQL触发器是与表关联的存储程序,当INSERT/UPDATE/DELETE事件发生时自动执行,用于维护数据一致性、日志记录和校验,优点包括自动执行... 目录触发器的概念：创建触www.chinasem.cn发器：查看触发器：查看当前数据库的所有触发器的定
阅读更多...
创建springBoot模块没有目录结构的解决方案

创建springBoot模块没有目录结构的解决方案

《创建springBoot模块没有目录结构的解决方案》2023版IntelliJIDEA创建模块时可能出现目录结构识别错误,导致文件显示异常,解决方法为选择模块后点击确认,重新校准项目结构设置,确保源... 目录创建spChina编程ringBoot模块没有目录结构解决方案总结创建springBoot模块没有目录
阅读更多...
IntelliJ IDEA2025创建SpringBoot项目的实现步骤

IntelliJ IDEA2025创建SpringBoot项目的实现步骤

《IntelliJIDEA2025创建SpringBoot项目的实现步骤》本文主要介绍了IntelliJIDEA2025创建SpringBoot项目的实现步骤,文中通过示例代码介绍的非常详细,对大家... 目录一、创建 Spring Boot 项目1. 新建项目2. 基础配置3. 选择依赖4. 生成项目5.
阅读更多...
Linux线程之线程的创建、属性、回收、退出、取消方式

Linux线程之线程的创建、属性、回收、退出、取消方式

《Linux线程之线程的创建、属性、回收、退出、取消方式》文章总结了线程管理核心知识：线程号唯一、创建方式、属性设置（如分离状态与栈大小）、回收机制（join/detach）、退出方法（返回/pthr... 目录1. 线程号2. 线程的创建3. 线程属性4. 线程的回收5. 线程的退出6. 线程的取消7.
阅读更多...
创建Java keystore文件的完整指南及详细步骤

创建Java keystore文件的完整指南及详细步骤

《创建Javakeystore文件的完整指南及详细步骤》本文详解Java中keystore的创建与配置,涵盖私钥管理、自签名与CA证书生成、SSL/TLS应用,强调安全存储及验证机制,确保通信加密和... 目录1. 秘密键（私钥）的理解与管理私钥的定义与重要性私钥的管理策略私钥的生成与存储2. 证书的创建与
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2